数学卷·2018届安徽省巢湖市高二上学期期末数学试卷（文科）+（解析版）

数学卷·2018届安徽省巢湖市高二上学期期末数学试卷（文科）+（解析版）

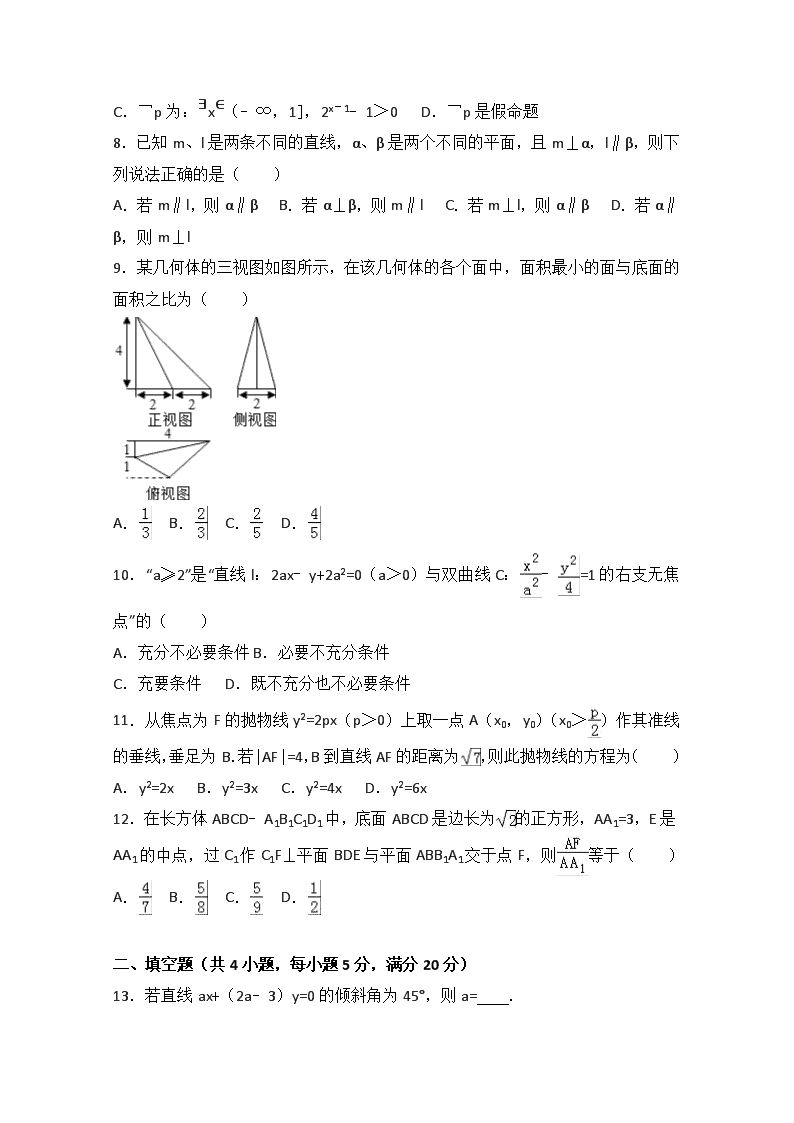
‎2016-2017学年安徽省巢湖市高二（上）期末数学试卷（文科）‎ ‎　‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1．椭圆+y2=1的焦距为（　　）‎ A．1 B．2 C． D．2‎ ‎2．命题“若x＞2，则x2﹣3x+2＞0”的否命题是（　　）‎ A．若x2﹣3x+2＜0，则x≥2 B．若x≤2，则x2﹣3x+2≤0‎ C．若x2﹣3x+2＜0，则x≥2 D．若x2﹣3x+2≤0，则x≤2‎ ‎3．已知，若直线xcosθ+2y+1=0与直线x﹣ysin2θ﹣3=0垂直，则sinθ等于（　　）‎ A． B． C． D．‎ ‎4．以（2，﹣1）为圆心且与直线x﹣y+1=0相切的圆的方程为（　　）‎ A．（x﹣2）2+（y+1）2=8 B．（x﹣2）2+（y+1）2=4 C．（x+2）2+（y﹣1）2=8 D．（x+2）2+（y﹣1）2=4‎ ‎5．若以双曲线﹣=1（a＞0）的左、右焦点和点（2，1）为顶点的三角形为直角三角形，则此双曲线的实轴长为（　　）‎ A．1 B．2 C．3 D．6‎ ‎6．在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为（　　）‎ A． B． C． D．‎ ‎7．已知命题p：∀x∈（1，+∞），2x﹣1﹣1＞0，则下列叙述正确的是（　　）‎ A．￢p为：∀x∈（1，+∞），2x﹣1﹣1≤0 B．￢p为：∃x∈（1，+∞），2x﹣1﹣1＜0‎ C．￢p为：∃x∈（﹣∞，1]，2x﹣1﹣1＞0 D．￢p是假命题 ‎8．已知m、l是两条不同的直线，α、β是两个不同的平面，且m⊥α，l∥β，则下列说法正确的是（　　）‎ A．若m∥l，则α∥β B．若α⊥β，则m∥l C．若m⊥l，则α∥β D．若α∥β，则m⊥l ‎9．某几何体的三视图如图所示，在该几何体的各个面中，面积最小的面与底面的面积之比为（　　）‎ A． B． C． D．‎ ‎10．“a≥2”是“直线l：2ax﹣y+2a2=0（a＞0）与双曲线C：﹣=1的右支无焦点”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎11．从焦点为F的抛物线y2=2px（p＞0）上取一点A（x0，y0）（x0＞）作其准线的垂线，垂足为B．若|AF|=4，B到直线AF的距离为，则此抛物线的方程为（　　）‎ A．y2=2x B．y2=3x C．y2=4x D．y2=6x ‎12．在长方体ABCD﹣A1B1C1D1中，底面ABCD是边长为的正方形，AA1=3，E是AA1的中点，过C1作C1F⊥平面BDE与平面ABB1A1交于点F，则等于（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（共4小题，每小题5分，满分20分）‎ ‎13．若直线ax+（2a﹣3）y=0的倾斜角为45°，则a=　　．‎ ‎14．已知焦点在x轴上的椭圆mx2+ny2=1的离心率为，则等于　　．‎ ‎15．等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A，B两点，；则C的实轴长为　　．‎ ‎16．在四棱锥P﹣ABCD中，底面ABCD是一直角梯形，BA⊥AD，AD∥BC，AB=2，BC=1，PA=3，AD=4，PA⊥底面ABCD，E是PD上一点，且CE∥平面PAB，则三棱锥C﹣ABE的体积为　　．‎ ‎　‎ 三、解答题（共6小题，满分70分）‎ ‎17．已知圆心为（3，4）的圆N被直线x=1截得的弦长为2．‎ ‎（1）求圆N的方程；‎ ‎（2）若过点D（3，6）的直线l被圆N截得的弦长为4，求直线l的斜率．‎ ‎18．如图，在三棱锥P﹣ABC中，平面PAC⊥平面ABC，∠BAC=60°，E，F分别是AP，AC的中点，点D在棱AB上，且AD=AC．求证：‎ ‎（1）EF∥平面PBC；‎ ‎（2）平面DEF⊥平面PAC．‎ ‎19．设p：以抛物线C：y2=kx（k＞0）的焦点F和点M（1，）为端点的线段与抛物线C有交点，q：方程+=1表示焦点在x轴上的椭圆．‎ ‎（1）若q为真，求实数k的取值范围；‎ ‎（2）若p∧q为假，p∨q为真，求实数k的取值范围．‎ ‎20．如图所示，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AF=BF，EC∥FD，FD⊥底面ABCD，M是AB的中点．‎ ‎（1）求证：平面CFM⊥平面BDF；‎ ‎（2）点N在CE上，EC=2，FD=3，当CN为何值时，MN∥平面BEF．‎ ‎21．已知与直线相切的动圆M与圆外切．‎ ‎（1）求圆心M的轨迹L的方程；‎ ‎（2）若倾斜角为且经过点（2.0）的直线l与曲线L相交于两点A、B，求证：OA⊥OB．‎ ‎22．已知椭圆C： +=1（a＞b＞0）的右焦点为F（1，0），短轴的一个端点B到F的距离等于焦距．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）过点F的直线l与椭圆C交于不同的两点M，N，是否存在直线l，使得△BFM与△BFN的面积比值为2？若存在，求出直线l的方程；若不存在，说明理由．‎ ‎　‎ ‎2016-2017学年安徽省巢湖市高二（上）期末数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（共12小题，每小题5分，满分60分）‎ ‎1．椭圆+y2=1的焦距为（　　）‎ A．1 B．2 C． D．2‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】根据题意，由椭圆的标准方程可得a2=2，b2=1，由椭圆的性质可得c的值，进而由椭圆焦距的定义可得答案．‎ ‎【解答】解：根据题意，椭圆的标准方程为： +=1，‎ 则有a2=2，b2=1，‎ 则c==1，‎ 故该椭圆的焦距为2c=2；‎ 故选：B．‎ ‎　‎ ‎2．命题“若x＞2，则x2﹣3x+2＞0”的否命题是（　　）‎ A．若x2﹣3x+2＜0，则x≥2 B．若x≤2，则x2﹣3x+2≤0‎ C．若x2﹣3x+2＜0，则x≥2 D．若x2﹣3x+2≤0，则x≤2‎ ‎【考点】四种命题．‎ ‎【分析】根据已知中的原命题，结合四种命题的定义，可得答案．‎ ‎【解答】解：命题“若x＞2，则x2﹣3x+2＞0”的否命题是“若x≤2，则x2﹣3x+2≤0”，‎ 故选：B ‎　‎ ‎3．已知，若直线xcosθ+2y+‎ ‎1=0与直线x﹣ysin2θ﹣3=0垂直，则sinθ等于（　　）‎ A． B． C． D．‎ ‎【考点】直线的一般式方程与直线的垂直关系．‎ ‎【分析】利用直线与直线垂直的性质求解．‎ ‎【解答】解：由题意可得﹣•=﹣1，‎ 即sinθ=，‎ 故选：D ‎　‎ ‎4．以（2，﹣1）为圆心且与直线x﹣y+1=0相切的圆的方程为（　　）‎ A．（x﹣2）2+（y+1）2=8 B．（x﹣2）2+（y+1）2=4 C．（x+2）2+（y﹣1）2=8 D．（x+2）2+（y﹣1）2=4‎ ‎【考点】圆的标准方程．‎ ‎【分析】直线与圆相切，则圆心到直线的距离即为圆的半径．利用点到直线的距离公式求出半径即可得到圆的方程．‎ ‎【解答】解：圆心（2，﹣1）到直线x﹣y+1=0的距离为d==2，‎ ‎∵圆与直线直线x﹣y+1=0相切，‎ ‎∴半径r=2．‎ ‎∴所求圆的方程为（x﹣2）2+（y+1）2=8．‎ 故选A．‎ ‎　‎ ‎5．若以双曲线﹣=1（a＞0）的左、右焦点和点（2，1）为顶点的三角形为直角三角形，则此双曲线的实轴长为（　　）‎ A．1 B．2 C．3 D．6‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】由题意，以双曲线﹣=1（a＞0）的左、右焦点和点（2，1）为顶点的三角形为直角三角形，可得（2﹣c，1）•（2+c，1）=0，求出c，即可求出a．‎ ‎【解答】解：由题意，以双曲线﹣=1（a＞0）的左、右焦点和点（2，1）为顶点的三角形为直角三角形，‎ ‎∴（2﹣c，1）•（2+c，1）=0，‎ ‎∴4﹣c2+1=0，‎ ‎∴c=，‎ ‎∴2a=2=2．‎ 故选：B．‎ ‎　‎ ‎6．在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为（　　）‎ A． B． C． D．‎ ‎【考点】简单空间图形的三视图．‎ ‎【分析】由俯视图和正视图可以得到几何体是一个简单的组合体，是由一个三棱锥和被轴截面截开的半个圆锥组成，根据组合体的结构特征，得到组合体的侧视图．‎ ‎【解答】解：由俯视图和正视图可以得到几何体是一个简单的组合体，‎ 是由一个三棱锥和被轴截面截开的半个圆锥组成，‎ ‎∴侧视图是一个中间有分界线的三角形，‎ 故选D．‎ ‎　‎ ‎7．已知命题p：∀x∈（1，+∞），2x﹣1﹣1＞0，则下列叙述正确的是（　　）‎ A．￢p为：∀x∈（1，+∞），2x﹣1﹣1≤0 B．￢p为：∃x∈（1，+∞），2x﹣1﹣1＜0‎ C．￢p为：∃x∈（﹣∞，1]，2x﹣1﹣1＞0 D．￢p是假命题 ‎【考点】命题的否定．‎ ‎【分析】根据已知中原命题，写出命题的否定，并判断其真假，可得答案．‎ ‎【解答】解：∵命题p：∀x∈（1，+∞），2x﹣1﹣1＞0，‎ ‎∴命题￢p为：∃x∈（1，+∞），2x﹣1﹣1≤0；‎ ‎∵f（x）=2x﹣1﹣1在（1，+∞）为增函数，‎ ‎∴f（x）＞f（1）=0‎ 故p是真命题，即¬p是假命题．‎ 故选：D ‎　‎ ‎8．已知m、l是两条不同的直线，α、β是两个不同的平面，且m⊥α，l∥β，则下列说法正确的是（　　）‎ A．若m∥l，则α∥β B．若α⊥β，则m∥l C．若m⊥l，则α∥β D．若α∥β，则m⊥l ‎【考点】空间中直线与平面之间的位置关系．‎ ‎【分析】根据空间直线和平面、平面和平面平行或垂直的判定定理和性质定理分别进行判断即可．‎ ‎【解答】解：若m∥l，m⊥α，则l⊥α，又l∥β，则α⊥β，即A不正确；‎ 若α⊥β，则m、l位置不确定，即B不正确；‎ 若m⊥l，则α∥β或α，β相交，即C 不正确；‎ 若m⊥α，α∥β，则m⊥β，又l∥β，则m⊥l，即D正确，‎ 故选D．‎ ‎　‎ ‎9．某几何体的三视图如图所示，在该几何体的各个面中，面积最小的面与底面的面积之比为（　　）‎ A． B． C． D．‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】由三视图知，该几何体是高为4的四棱锥，计算出最小面的面积与最大面是底面的面积，求出比值即可．‎ ‎【解答】解：由三视图可知，该几何体是高为4的四棱锥，‎ 计算可得最小面的面积为×1×4=2，‎ 最大的是底面面积为（2+4）×2﹣×2×1=5，‎ 所以它们的比是．‎ 故选：C．‎ ‎　‎ ‎10．“a≥2”是“直线l：2ax﹣y+2a2=0（a＞0）与双曲线C：﹣=1的右支无焦点”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】求出直线l：2ax﹣y+2a2=0（a＞0）与双曲线C：﹣=1的右支无焦点的充分必要条件，结合集合的包含关系判断即可．‎ ‎【解答】解：∵直线l：2ax﹣y+2a2=0（a＞0）与双曲线C：﹣=1的右支无焦点，‎ ‎∴直线l的斜率不小于双曲线C的渐近线y=x的斜率，‎ 即2a≥，∵a＞0，‎ ‎∴a≥1，‎ 故a≥2是a≥1的充分不必要条件，‎ 故选：A．‎ ‎　‎ ‎11．从焦点为F的抛物线y2=2px（p＞0）上取一点A（x0，y0）（x0＞）作其准线的垂线，垂足为B．若|AF|=4，B到直线AF的距离为，则此抛物线的方程为（　　）‎ A．y2=2x B．y2=3x C．y2=4x D．y2=6x ‎【考点】抛物线的简单性质．‎ ‎【分析】设B到直线AF的距离为BC=，求出cos∠BAF=，设F到AB的距离为AD，则|AD|=|AF|cos∠BAF=3，即可得出结论．‎ ‎【解答】解：设B到直线AF的距离为BC=，‎ 由|AF|=|AB|=4，可得sin∠BAF=，‎ ‎∴cos∠BAF=，‎ 设F到AB的距离为AD，则|AD|=|AF|cos∠BAF=3，∴p+|AD|=4，‎ ‎∴p=1，‎ ‎∴此抛物线的方程为y2=2x．‎ 故选A．‎ ‎　‎ ‎12．在长方体ABCD﹣A1B1C1D1中，底面ABCD是边长为的正方形，AA1=3，E是AA1的中点，过C1作C1F⊥平面BDE与平面ABB1A1交于点F，则等于（　　）‎ A． B． C． D．‎ ‎【考点】棱柱的结构特征．‎ ‎【分析】连结AC、BD，交于点O，当C1F与EO垂直时，C1F⊥平面BDE，从而F∈AA1，△C1A1F∽△EAO，由此能求出的值．‎ ‎【解答】解：连结AC、BD，交于点O，‎ ‎∵四边形ABCD是正方形，AA1⊥底面ABCD，‎ ‎∴BD⊥平面ACC1A1，‎ 则当C1F与EO垂直时，C1F⊥平面BDE，‎ ‎∵F∈平面ABB1A1，∴F∈AA1，‎ ‎ 在矩形ACC1A1中，△C1A1F∽△EAO，‎ 则=，‎ ‎∵A1C1=2AO=，AE=，‎ ‎∴A1F=，∴AF=，∴=．‎ 故选：C．‎ ‎　‎ 二、填空题（共4小题，每小题5分，满分20分）‎ ‎13．若直线ax+（2a﹣3）y=0的倾斜角为45°，则a=　1　．‎ ‎【考点】直线的倾斜角．‎ ‎【分析】利用倾斜角先求出斜率，由此能求出a的值．‎ ‎【解答】解：∵直线ax+（2a﹣3）y=0的倾斜角为45°，‎ ‎∴=tan45°=1．‎ 解得a=1，‎ 故答案为：1‎ ‎　‎ ‎14．已知焦点在x轴上的椭圆mx2+ny2=1的离心率为，则等于　　．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】焦点在x轴上的椭圆mx2+ny2=1中：a2=，b2=，e2=1﹣=1﹣=，可得m：n ‎【解答】解：焦点在x轴上的椭圆mx2+ny2=1中：‎ a2=，b2=，e2=1﹣=1﹣=，∴．‎ 故答案为：‎ ‎　‎ ‎15．等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A，B两点，；则C的实轴长为　4　．‎ ‎【考点】双曲线的简单性质；抛物线的简单性质．‎ ‎【分析】设出双曲线方程，求出抛物线的准线方程，利用，即可求得结论．‎ ‎【解答】解：设等轴双曲线C的方程为x2﹣y2=λ．（1）‎ ‎∵抛物线y2=16x，2p=16，p=8，∴=4．‎ ‎∴抛物线的准线方程为x=﹣4．‎ 设等轴双曲线与抛物线的准线x=﹣4的两个交点A（﹣4，y），B（﹣4，﹣y）（y＞0），‎ 则|AB|=|y﹣（﹣y）|=2y=4，∴y=2．‎ 将x=﹣4，y=2代入（1），得（﹣4）2﹣（2）2=λ，∴λ=4‎ ‎∴等轴双曲线C的方程为x2﹣y2=4，即 ‎∴C的实轴长为4．‎ 故答案为：4‎ ‎　‎ ‎16．在四棱锥P﹣ABCD中，底面ABCD是一直角梯形，BA⊥AD，AD∥‎ BC，AB=2，BC=1，PA=3，AD=4，PA⊥底面ABCD，E是PD上一点，且CE∥平面PAB，则三棱锥C﹣ABE的体积为　　．‎ ‎【考点】棱柱、棱锥、棱台的体积．‎ ‎【分析】过点C作CF⊥AD于F，过F作EF⊥AD交PD于E，则EF⊥平面ABCD，三棱锥C﹣ABE的体积VC﹣ABE=VE﹣ABC，由此能求出结果．‎ ‎【解答】解：过点C作CF⊥AD于F，‎ 过F作EF⊥AD交PD于E，‎ 则EF⊥平面ABCD，‎ ‎∵PA⊥底面ABCD，∴EF∥PA，‎ ‎∵BA⊥AD，CF⊥AD，∴AB∥FC，‎ ‎∵PA∩AB=A，EF∩FC=F，PA，AB⊂平面PAB，EF，FC⊂平面EFC，‎ ‎∴平面PAB∥平面EFC，‎ ‎∵CE⊂平面EFC，∴CE∥平面PAB，‎ ‎∴EF=PA=，‎ ‎∴三棱锥C﹣ABE的体积VC﹣ABE=VE﹣ABC==．‎ 故答案为：．‎ ‎　‎ 三、解答题（共6小题，满分70分）‎ ‎17．已知圆心为（3，4）的圆N被直线x=1截得的弦长为2．‎ ‎（1）求圆N的方程；‎ ‎（2）若过点D（3，6）的直线l被圆N截得的弦长为4，求直线l的斜率．‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】（1）求出圆的半径，即可求圆N的方程；‎ ‎（2）根据题意得到直线l斜率存在，设为k，表示出直线l方程，利用点到直线的距离公式表示出圆心到直线l的距离d，根据r与弦长，利用垂径定理及勾股定理列出关于k的方程，求出方程的解得到k的值即可．‎ ‎【解答】解：（1）由题意，圆心到直线的距离为3﹣1=2，‎ ‎∵圆N被直线x=1截得的弦长为2，‎ ‎∴圆的半径r==3，‎ ‎∴圆N的方程为（x﹣3）2+（y﹣4）2=9；‎ ‎（2）设直线l方程为y﹣6=k（x﹣3），即kx﹣y﹣3k+6=0，‎ ‎∵圆心（3，4）到直线l的距离d=，r=3，弦长为4，‎ ‎∴4=2，化简得1+k2=4，解得：k=±．‎ ‎　‎ ‎18．如图，在三棱锥P﹣ABC中，平面PAC⊥平面ABC，∠BAC=60°，E，F分别是AP，AC的中点，点D在棱AB上，且AD=AC．求证：‎ ‎（1）EF∥平面PBC；‎ ‎（2）平面DEF⊥平面PAC．‎ ‎【考点】平面与平面垂直的判定；直线与平面平行的判定．‎ ‎【分析】（1）利用三角形中位线定理推导出EF∥PC，由此能证明EF∥平面PBC．‎ ‎（2）由已知条件推导出△ACD为正三角形，DF⊥AC，从而得到DF⊥平面PAC，由此能证明平面DEF⊥平面PAC．‎ ‎【解答】证明：（1）在△PAC中，因为E，F分别是AP，AC的中点，‎ 所以EF∥PC．…‎ 又因为EF⊄平面PBC，PC⊂平面PBC，‎ 所以EF∥平面PBC．…‎ ‎（2）连结CD．因为∠BAC=60°，AD=AC，‎ 所以△ACD为正三角形．‎ 因为F是AC的中点，所以DF⊥AC．…‎ 因为平面PAC⊥平面ABC，DF⊂平面ABC，‎ 平面PAC∩平面ABC=AC，‎ 所以DF⊥平面PAC． …‎ 因为DF⊂平面DEF，‎ 所以平面DEF⊥平面PAC．…‎ ‎　‎ ‎19．设p：以抛物线C：y2=kx（k＞0）的焦点F和点M（1，）为端点的线段与抛物线C有交点，q：方程+=1表示焦点在x轴上的椭圆．‎ ‎（1）若q为真，求实数k的取值范围；‎ ‎（2）若p∧q为假，p∨q为真，求实数k的取值范围．‎ ‎【考点】抛物线的简单性质；复合命题的真假．‎ ‎【分析】（1）q为真，则13﹣k2＞2k﹣2＞0，即可求实数k的取值范围；‎ ‎（2）若p为真，则M在抛物线C上或外部，p∧q为假，p∨q为真，p，q一真一假，即可求出m的取值范围．‎ ‎【解答】解：（1）q为真，则13﹣k2＞2k﹣2＞0，解得1＜k＜3；‎ ‎（2）若p为真，则M在抛物线C上或外部，‎ ‎∴x=1时，y=，∴0＜k≤2．‎ ‎∵p∧q为假，p∨q为真，‎ ‎∴p，q一真一假，‎ p真q假，则0＜k≤1；p假q真，则2＜k＜3，‎ 综上所述，0＜k≤1或2＜k＜3．‎ ‎　‎ ‎20．如图所示，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AF=BF，EC∥FD，FD⊥底面ABCD，M是AB的中点．‎ ‎（1）求证：平面CFM⊥平面BDF；‎ ‎（2）点N在CE上，EC=2，FD=3，当CN为何值时，MN∥平面BEF．‎ ‎【考点】直线与平面平行的判定；平面与平面垂直的判定．‎ ‎【分析】（1）推导出四边形BCDM是正方形，从而BD⊥CM，又DF⊥CM，由此能证明CM⊥平面BDF．‎ ‎（2）过N作NO∥EF，交EF于O，连结MO，则四边形EFON是平行四边形，连结OE，则四边形BMON是平行四边形，由此能推导出N是CE的中点时，MN∥平面BEF．‎ ‎【解答】证明：（1）∵FD⊥底面ABCD，∴FD⊥AD，FD⊥BD ‎∵AF=BF，∴△ADF≌△BDF，∴AD=BD，‎ 连接DM，则DM⊥AB，‎ ‎∵AB∥CD，∠BCD=90°，‎ ‎∴四边形BCDM是正方形，∴BD⊥CM，‎ ‎∵DF⊥CM，∴CM⊥平面BDF．‎ 解：（2）当CN=1，即N是CE的中点时，MN∥平面BEF．‎ 证明如下：‎ 过N作NO∥EF，交ED于O，连结MO，‎ ‎∵EC∥FD，∴四边形EFON是平行四边形，‎ ‎∵EC=2，FD=3，∴OF=1，∴OD=2，‎ 连结OE，则OE∥DC∥MB，且OE=DC=MB，‎ ‎∴四边形BMOE是平行四边形，则OM∥BE，又OM∩ON=O，‎ ‎∴平面OMN∥平面BEF，‎ ‎∵MN⊂平面OMN，∴MN∥平面BEF．‎ ‎　‎ ‎21．已知与直线相切的动圆M与圆外切．‎ ‎（1）求圆心M的轨迹L的方程；‎ ‎（2）若倾斜角为且经过点（2.0）的直线l与曲线L相交于两点A、B，求证：OA⊥OB．‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】（1）确定点M到点与直线的距离相等，即可求圆心M的轨迹L的方程；‎ ‎（2）直线l的方程为y=x﹣2，联立y2=2x得x2﹣6x+4=0，证明=0，即可证明结论．‎ ‎【解答】解：（1）设动圆M的半径为r，‎ ‎∵圆M与圆外切，∴，…‎ ‎∵圆M与直线相切，∴圆心M到直线的距离为r，…‎ 则圆心M到直线的距离为，…‎ ‎∴点M到点与直线的距离相等，…‎ 即圆心M的轨迹方程是抛物线y2=2x…‎ ‎（2）直线l的方程为y=x﹣2，联立y2=2x得x2﹣6x+4=0，‎ 设A（x1，y1），B（x2，y2），则x1+x2=6，x1x2=4…‎ ‎∵=x1x2+y1y2=2x1x2﹣2（x1+x2）+4=0，‎ ‎∴OA⊥OB…‎ ‎　‎ ‎22．已知椭圆C： +=1（a＞b＞0）的右焦点为F（1，0），短轴的一个端点B到F的距离等于焦距．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）过点F的直线l与椭圆C交于不同的两点M，N，是否存在直线l，使得△BFM与△BFN的面积比值为2？若存在，求出直线l的方程；若不存在，说明理由．‎ ‎【考点】直线与圆锥曲线的综合问题．‎ ‎【分析】（Ⅰ）根据椭圆C： +=1（a＞b＞0）的右焦点为F（1，0），短轴的一个端点B到F的距离等于焦距，求出几何量，即可求椭圆C的方程；‎ ‎（Ⅱ）△BFM与△BFN的面积比值为2等价于FM与FN比值为2，分类讨论，设直线l的方程为y=k（x﹣1），代入椭圆方程，消x并整理，利用韦达定理，根据FM与FN比值为2，即可求得直线方程．‎ ‎【解答】解：（Ⅰ）由已知得c=1，a=2c=2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎∴=，‎ ‎∴椭圆C的方程为﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎（Ⅱ）△BFM与△BFN的面积比值为2等价于FM与FN比值为2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 当直线l斜率不存在时，FM与FN比值为1，不符合题意，舍去；﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 当直线l斜率存在时，设直线l的方程为y=k（x﹣1），‎ 直线l的方程代入椭圆方程，消x并整理得（3+4k2）y2+6ky﹣9k2=0﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 设M（x1，y1），N（x2，y2），则y1+y2=﹣①，y1y2=﹣②﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ 由FM与FN比值为2得y1=﹣2y2③‎ 由①②③解得k=±，‎ 因此存在直线l：y=±（x﹣1）使得△BFM与△BFN的面积比值为2﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎　‎