上海教育高中数学二上矩阵运算

上海教育高中数学二上矩阵运算

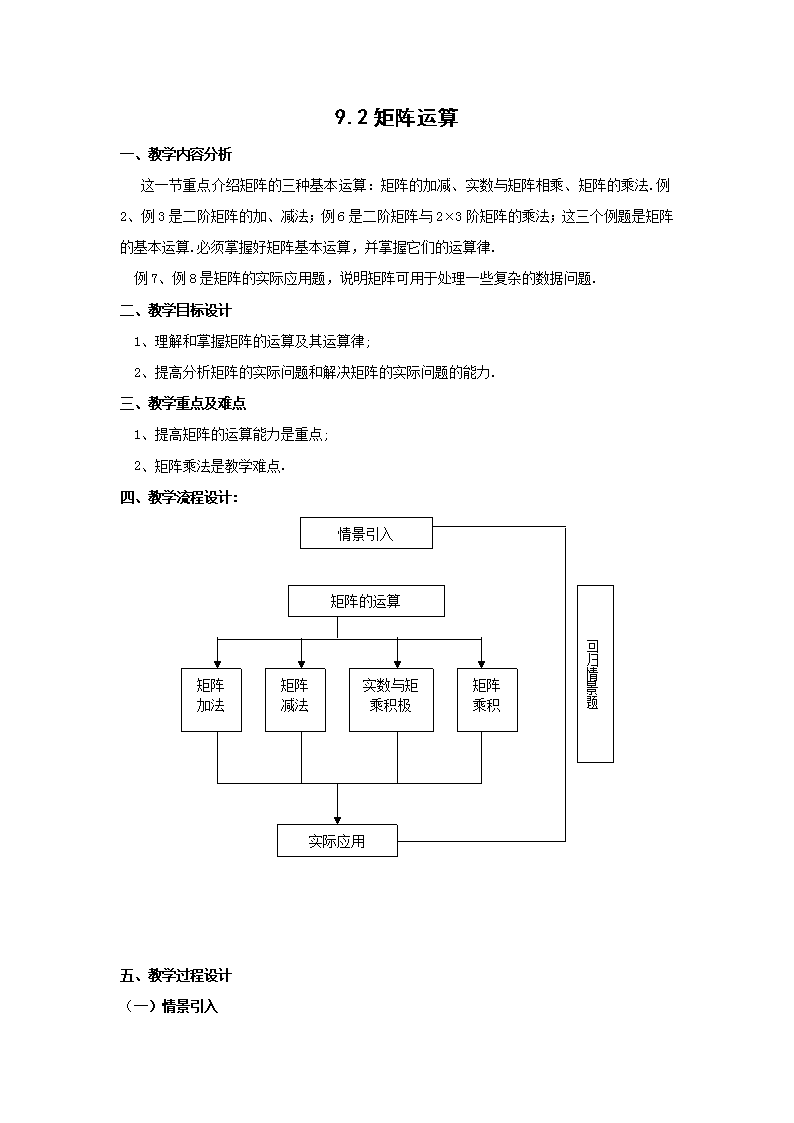
‎9.2矩阵运算 一、教学内容分析 ‎ 这一节重点介绍矩阵的三种基本运算：矩阵的加减、实数与矩阵相乘、矩阵的乘法.例2、例3是二阶矩阵的加、减法；例6是二阶矩阵与23阶矩阵的乘法；这三个例题是矩阵的基本运算.必须掌握好矩阵基本运算，并掌握它们的运算律.‎ ‎ 例7、例8是矩阵的实际应用题，说明矩阵可用于处理一些复杂的数据问题.‎ 二、教学目标设计 ‎ 1、理解和掌握矩阵的运算及其运算律;‎ ‎ 2、提高分析矩阵的实际问题和解决矩阵的实际问题的能力.‎ 三、教学重点及难点 ‎ 1、提高矩阵的运算能力是重点;‎ ‎ 2、矩阵乘法是教学难点.‎ 四、教学流程设计:‎ 情景引入 矩阵的运算 矩阵加法 矩阵减法 实数与矩乘积极 矩阵乘积 实际应用 回归情景题 五、教学过程设计 ‎（一）情景引入 小王、小李在两次数学考试中答对题数如下表表示：‎ ‎ 题型 答题21世纪教育网21世纪教育网 姓 数 ‎ 名[网 期中21世纪教育网 期末 填空题 选择题 解答题 填空题 选择题 解答题 小王 ‎10‎ ‎3‎ ‎2‎ ‎8‎ ‎4‎ ‎4‎ 小李 ‎9‎ ‎5‎ ‎3‎ ‎7‎ ‎3‎ ‎3‎ 填空题每题4分，选择题4分，解答题每题10分.‎ 1、 观察：‎ 2、 思考（1）：如何用矩阵表示他们的答对题数？他们期中、期末的成绩？‎ 思考（2）：如果期中占40%，期末占60%，求两同学的总评成绩 3、 讨论：今天如何通过矩阵运算来研究上述问题？‎ ‎（二）学习新课 ‎1、矩阵的加法 ‎（1）引入 记期中成绩答题数为A 期末答题数为B ‎ ‎ 确定两次考试的小王，小李的各题型答题总数的矩阵C ‎ （2）矩阵的和（差）‎ ‎ 当两个矩阵A，B的维数相同时，将它们各位置上的元素加（减）所得到的矩阵称为矩阵A，B的和（差）,记作：A+B（A-B）‎ ‎ （3）运算律 ‎ 加法运算律：A+B=B+A ‎ 加法结合律：（A+B）+C=A+（B+C）‎ ‎ （4）举例：P80 例2，例3‎ ‎2、数乘矩阵 ‎（1）引入：计算小王、小李各题型平均答题数的矩阵 ‎ ‎ ‎（2）矩阵与实数的积 ‎ 设为任意实数，把矩阵A的所有元素与相乘得到的矩阵叫做矩阵A与实数的乘积矩阵.记作：A ‎（3）运算律：（为实数）‎ ‎ 分配律： ；‎ ‎ 结合律：‎ ‎（4）举例：P81 例4‎ ‎3、矩阵的乘积 ‎（1）引入：P83的两次线性变换 ‎（2）矩阵的乘积：‎ 一般，设A是阶矩阵，B是阶矩阵，设C为矩阵 如果矩阵C中第i行第j列元素是矩阵A第i个行向量与矩阵B的第j个列向量的数量积，那么C矩阵叫做A与B的乘积.记作：C=AB ‎（3）运算律 ‎ 分配律：，‎ ‎ 结合律：，‎ 注：交换律不成立，即 ‎（4）举例 例1（1） （2）‎ ‎ （3） （4）‎ ‎ （5）‎ 答案：1） 2) 3) 4) 5) ‎ 注：（1）（2）结果不同.（3）（4）结果不同，说明矩阵乘法交换律不成立.‎ 例2：P85 例8‎ ‎（三）回归情景：讨论如何使用矩阵运算进一步研究小王、小李的考试成绩.‎ ‎（四）课堂练习：P83，P86‎ ‎（五）课堂小结 ‎（六）布置作业：见练习册 七：教学设计说明 1、 通过情景题小王、小李的成绩情况引入矩阵运算，说明矩阵运算的重要性.‎ 2、 课堂按“加减法→数乘→乘法”展开研究，层层深入，重在掌握2阶，3阶的矩阵的基本运算.‎ 3、 对矩阵运算律只进行总结，不进行证明.旨在今后学生能灵活地使用运算律进行运算.这里特别强调乘法的交换律不成立.这是学生思维上不易接受点，在过去的学习的实数运算、集合运算、向量运算的不同之处，必须引起重视.‎ 4、 加强了实际问题的分析，说明矩阵在实际问题中的重要运用.‎