2020_2021学年新教材高中数学第二章直线和圆的方程2
2.5.2
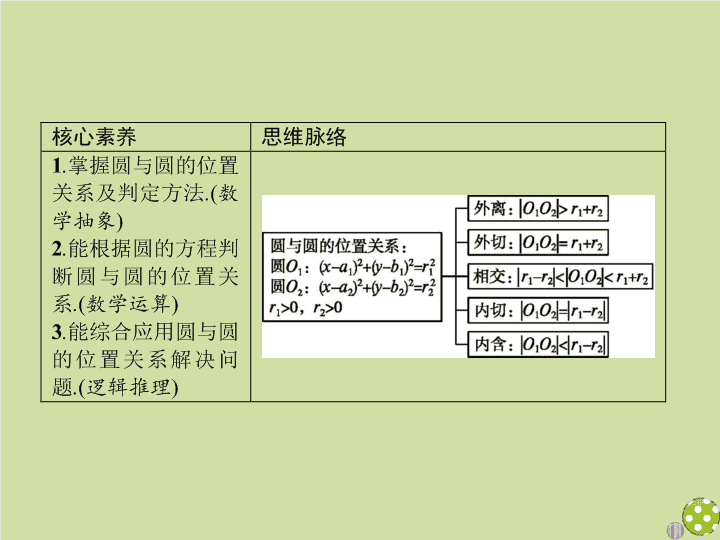
圆与圆的位置关系
激趣诱思
知识点拨
“
打水漂
”
游戏别名轻功水上漂、七点漂、漂瓦
,
是用扁形瓦片或石片
,
在手上呈水平放置后
,
用力飞出
,
石片擦水面飞行
,
石片碰水面后弹起再飞
,
石片不断在水面上向前弹跳
,
直至沉水
.
在这一过程中
,
石片与水面接触形成了一个个逐渐扩大的圆
,
这些圆在变化的过程中位置关系是怎样的
?
激趣诱思
知识点拨
圆与圆的位置关系的判定方法
1
.
几何法
:
激趣诱思
知识点拨
激趣诱思
知识点拨
微练习
(1)
判断下列两圆的位置关系
:
①
(
x+
2)
2
+
(
y-
2)
2
=
1
与
(
x-
2)
2
+
(
y-
5)
2
=
16
.
②
x
2
+y
2
+
6
x-
7
=
0
与
x
2
+y
2
+
6
y-
27
=
0
.
解
:
①
根据题意得
,
两圆的半径分别为
r
1
=
1
和
r
2
=
4,
两圆的圆心距
因为
d=r
1
+r
2
,
所以两圆外切
.
②
将两圆的方程化为标准方程
,
得
(
x+
3)
2
+y
2
=
16,
x
2
+
(
y+
3)
2
=
36,
故两圆的半径分别为
r
1
=
4
和
r
2
=
6
.
两圆的圆心距
激趣诱思
知识点拨
(2)
两圆
x
2
+y
2
=
1
和
(
x+
4)
2
+
(
y-a
)
2
=
25
相切
,
则实数
a
的值为
.
探究一
探究二
探究三
素养形成
当堂检测
判断两圆的位置关系
例
1
已知圆
C
1
:
x
2
+y
2
-
2
ax-
2
y+a
2
-
15
=
0(
a>
0),
圆
C
2
:
x
2
+y
2
-
4
ax-
2
y+
4
a
2
=
0(
a>
0)
.
试求
a
为何值时
,
两圆
C
1
,
C
2
的位置关系为
:
(1)
相切
;(2)
相交
;(3)
外离
;(4)
内含
?
思路分析
:
求出圆心距
,
与两半径的和或差比较求出
a
的值
.
探究一
探究二
探究三
素养形成
当堂检测
解
:
圆
C
1
,
C
2
的方程
,
经配方后可得
C
1
:(
x-a
)
2
+
(
y-
1)
2
=
16,
C
2
:(
x-
2
a
)
2
+
(
y-
1)
2
=
1,
∴
圆心
C
1
(
a
,1),
C
2
(2
a
,1),
半径
r
1
=
4,
r
2
=
1
.
(1)
当
|C
1
C
2
|=r
1
+r
2
=
5,
即
a=
5
时
,
两圆外切
;
当
|C
1
C
2
|=r
1
-r
2
=
3,
即
a=
3
时
,
两圆内切
.
(2)
当
3
<|C
1
C
2
|<
5,
即
3
5,
即
a>
5
时
,
两圆外离
.
(4)
当
|C
1
C
2
|<
3,
即
0
0),
由题知所求圆与圆
x
2
+y
2
-
2
x=
0
外切
,
探究一
探究二
探究三
素养形成
当堂检测
延伸探究
1
将本例变为
“
求与圆
x
2
+y
2
-
2
x=
0
外切
,
圆心在
x
轴上
,
且过点
(3
,
-
)
的圆的方程
”,
如何求
?
解
:
因为圆心在
x
轴上
,
所以可设圆心坐标为
(
a
,0),
设半径为
r
,
则所求圆的方程为
(
x-a
)
2
+y
2
=r
2
,
探究一
探究二
探究三
素养形成
当堂检测
延伸探究
2
将本例改为
“
若圆
x
2
+y
2
-
2
x=
0
与圆
x
2
+y
2
-
8
x-
8
y+m=
0
相外切
”,
试求实数
m
的值
.
反思感悟
处理两圆相切问题的两个步骤
(1)
定性
,
即必须准确把握是内切还是外切
,
若只是告诉相切
,
则必须考虑分两圆内切还是外切两种情况讨论
.
(2)
转化思想
,
即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值
(
内切时
)
或两圆半径之和
(
外切时
)
.
探究一
探究二
探究三
素养形成
当堂检测
圆系方程
经过两个圆的公共点可作无数个圆
,
这无数个圆可组成一个圆系
.
与已知圆有相同圆心的圆也可以组成一个圆系
,
等等
.
常见圆系方程有如下几种
:
1
.
过直线与圆的交点的圆系
:
过直线
Ax+By+C=
0
与圆
x
2
+y
2
+Dx+Ey+F=
0
交点的圆系方程为
x
2
+y
2
+Dx+Ey+F+
λ
(
Ax+By+C
)
=
0;
特别地
,
当直线与圆相切于点
P
时
,
上述方程表示与直线和圆都相切于点
P
的圆
.
2
.
过两个圆的交点的圆系
:
过两圆
x
2
+y
2
+D
1
x+E
1
y+F
1
=
0,
x
2
+y
2
+D
2
x+E
2
y+F
2
=
0
交点的圆系方程为
x
2
+y
2
+D
1
x+E
1
y+F
1
+
λ
(
x
2
+y
2
+D
2
x+E
2
y+F
2
)
=
0(
λ
≠
-
1),
此圆系不含圆
x
2
+y
2
+D
2
x+E
2
y+F
2
=
0
.
探究一
探究二
探究三
素养形成
当堂检测
3
.
同心圆系
:
与圆
x
2
+y
2
+Dx+Ey+F=
0
同心的圆系方程为
x
2
+y
2
+Dx+Ey+
λ
=
0;
或表示为与已知圆
(
x-a
)
2
+
(
y-b
)
2
=r
2
同心的圆系方程为
(
x-a
)
2
+
(
y-b
)
2
=R
2
(
其中
a
,
b
为定值
)
.
对圆系方程可作以下推广
:
对过两已知圆交点的圆系方程
,
当
λ
=-
1
时
,
得到
(
D
1
-D
2
)
x+
(
E
1
-E
2
)
y+F
1
-F
2
=
0,
此为两圆公共弦所在直线方程
.
因此
,
如果两圆相交
,
两圆的方程相减就得到两圆公共弦所在直线的方程
.
由此可推广
:
经过两曲线
f
(
x
,
y
)
=
0,
g
(
x
,
y
)
=
0
交点的曲线系方程为
f
(
x
,
y
)
+
λ
g
(
x
,
y
)
=
0
探究一
探究二
探究三
素养形成
当堂检测
典例
1
一圆过圆
x
2
+y
2
-
2
x=
0
和直线
x+
2
y-
3
=
0
的交点
,
且圆心在
y
轴上
,
则这个圆的方程是
(
)
A.
x
2
+y
2
-
4
x-
4
y+
6
=
0
B
.x
2
+y
2
+
4
y-
6
=
0
C.
x
2
+y
2
-
2
x=
0
D.
x
2
+y
2
+
4
x-
6
=
0
答案
:
B
探究一
探究二
探究三
素养形成
当堂检测
典例
2
已知两个圆
C
1
:
x
2
+y
2
=
4,
C
2
:
x
2
+y
2
-
2
x-
4
y+
4
=
0,
直线
l
:
x+
2
y=
0,
求经过
C
1
和
C
2
的交点且和
l
相切的圆的方程
.
探究一
探究二
探究三
素养形成
当堂检测
点评
圆与直线相切的问题可利用圆心到切线的距离等于半径列等式
.
求经过两圆交点的圆可考虑圆系
,
但要考虑
λ
≠
-
1,
另外由于圆系中不包括圆
x
2
+y
2
=
4,
因此应检验圆
x
2
+y
2
=
4
是否也满足条件
.
探究一
探究二
探究三
素养形成
当堂检测
1
.
两圆
x
2
+y
2
-
1
=
0
和
x
2
+y
2
-
4
x+
2
y-
4
=
0
的位置关系是
(
)
A
.
内切
B
.
相交
C
.
外切
D
.
外离
解析
:
圆
x
2
+y
2
-
1
=
0
表示以
O
1
(0,0)
点为圆心
,
以
R
1
=
1
为半径的圆
.
圆
x
2
+y
2
-
4
x+
2
y-
4
=
0
表示以
O
2
(2,
-
1)
点为圆心
,
以
R
2
=
3
为半径的圆
.
∵
|O
1
O
2
|=
,
∴
R
2
-R
1
<|O
1
O
2
|
查看更多