2015高考数学人教A版本（9-2简单几何体的表面积和体积）一轮复习学案

2015高考数学人教A版本（9-2简单几何体的表面积和体积）一轮复习学案

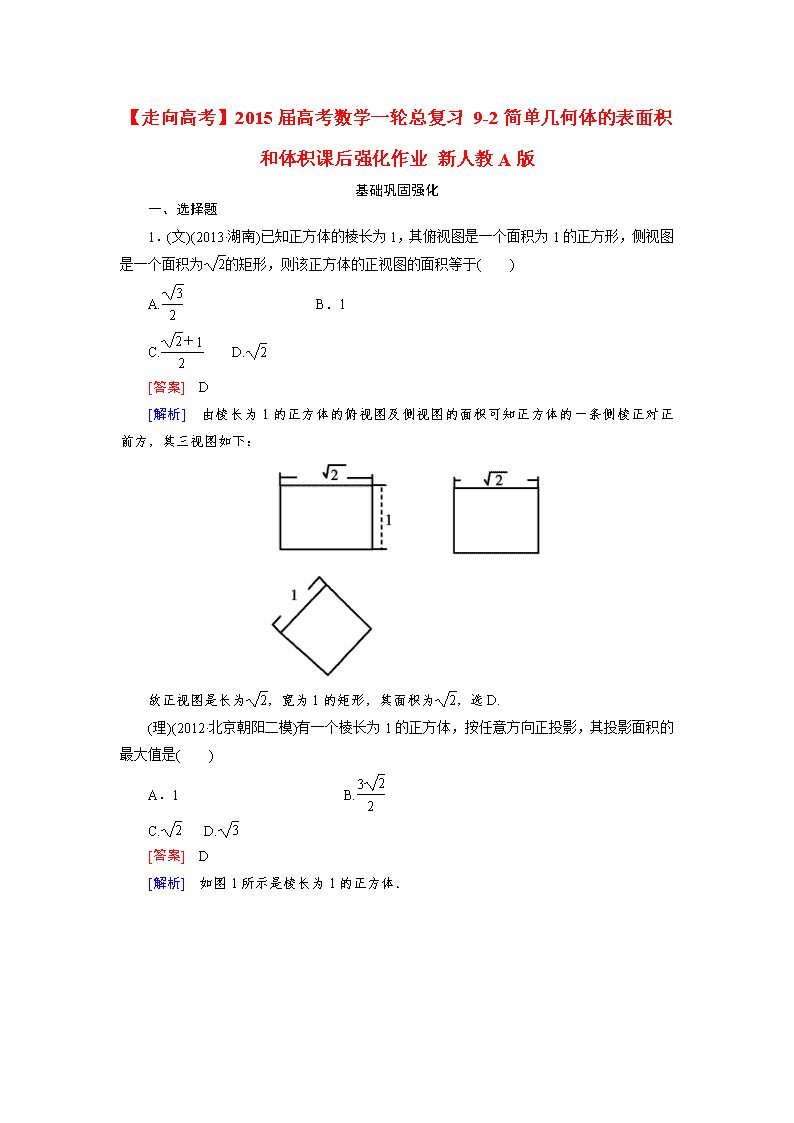
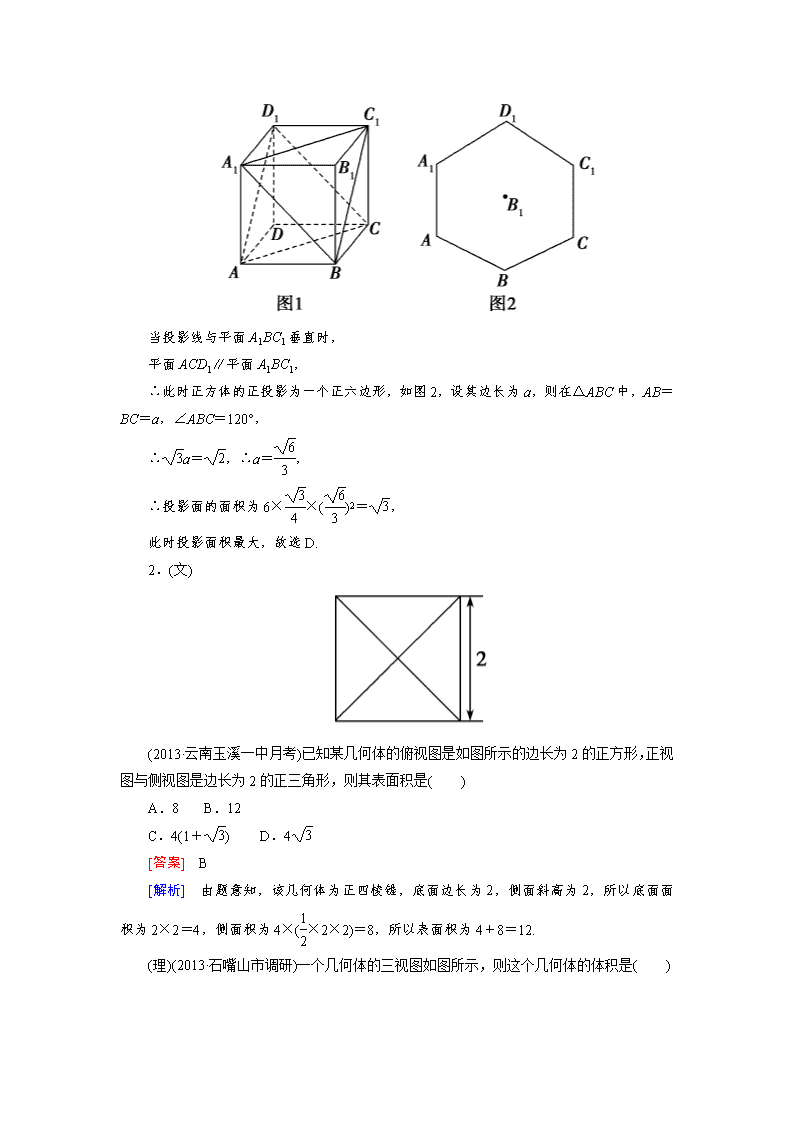
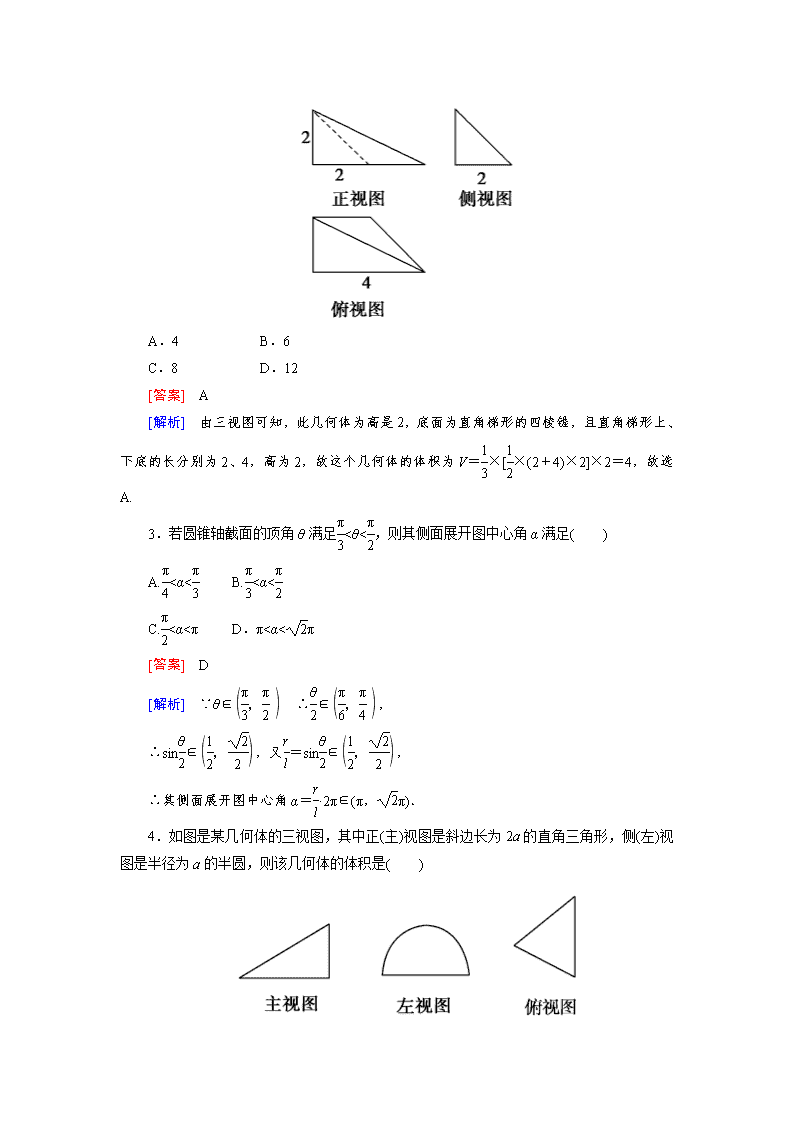
‎【走向高考】2015届高考数学一轮总复习 9-2简单几何体的表面积和体积课后强化作业 新人教A版 基础巩固强化 一、选择题 ‎1．(文)(2013·湖南)已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为的矩形，则该正方体的正视图的面积等于(　　)‎ A.　　　　　　　　 　 B．1‎ C. D. ‎[答案]　D ‎[解析]　由棱长为1的正方体的俯视图及侧视图的面积可知正方体的一条侧棱正对正前方，其三视图如下：‎ 故正视图是长为，宽为1的矩形，其面积为，选D.‎ ‎(理)(2012·北京朝阳二模)有一个棱长为1的正方体，按任意方向正投影，其投影面积的最大值是(　　)‎ A．1　　　　　　　　　　 B. C. D. ‎[答案]　D ‎[解析]　如图1所示是棱长为1的正方体．‎ 当投影线与平面A1BC1垂直时，‎ 平面ACD1∥平面A1BC1，‎ ‎∴此时正方体的正投影为一个正六边形，如图2，设其边长为a，则在△ABC中，AB＝BC＝a，∠ABC＝120°，‎ ‎∴a＝，∴a＝，‎ ‎∴投影面的面积为6××()2＝，‎ 此时投影面积最大，故选D.‎ ‎2．(文)‎ ‎(2013·云南玉溪一中月考)已知某几何体的俯视图是如图所示的边长为2的正方形，正视图与侧视图是边长为2的正三角形，则其表面积是(　　)‎ A．8 B．12‎ C．4(1＋) D．4 ‎[答案]　B ‎[解析]　由题意知，该几何体为正四棱锥，底面边长为2，侧面斜高为2，所以底面面积为2×2＝4，侧面积为4×(×2×2)＝8，所以表面积为4＋8＝12.‎ ‎(理)(2013·石嘴山市调研)一个几何体的三视图如图所示，则这个几何体的体积是(　　)‎ A．4　　　　 B．6　　　　‎ C．8　　　　 D．12‎ ‎[答案]　A ‎[解析]　由三视图可知，此几何体为高是2，底面为直角梯形的四棱锥，且直角梯形上、下底的长分别为2、4，高为2，故这个几何体的体积为V＝×[×(2＋4)×2]×2＝4，故选A.‎ ‎3．若圆锥轴截面的顶角θ满足<θ<，则其侧面展开图中心角α满足(　　)‎ A.<α< B.<α< C.<α<π D．π<α<π ‎[答案]　D ‎[解析]　∵θ∈　∴∈，‎ ‎∴sin∈，又＝sin∈，‎ ‎∴其侧面展开图中心角α＝·2π∈(π，π)．‎ ‎4．如图是某几何体的三视图，其中正(主)视图是斜边长为‎2a的直角三角形，侧(左)视图是半径为a的半圆，则该几何体的体积是(　　)‎ A.πa3 B.πa3‎ C.πa3 D．2πa3‎ ‎[答案]　A ‎[解析]　由侧(左)视图半圆可知，该几何体与圆柱、圆锥、球有关，结合正(主)视图是一个直角三角形知该几何体是沿中心轴线切开的半个圆锥将剖面放置在桌面上如图，‎ 由条件知，圆锥的母线长为‎2a，底面半径为a，‎ 故高h＝＝a，‎ 体积V＝×＝πa3.‎ ‎5．(文)侧棱长为4，底面边长为的正三棱柱的各顶点均在同一个球面上，则该球的表面积为(　　)‎ A．76π B．68π C．20π D．9π ‎[答案]　C ‎[解析]　设球心为O′，如图，球半径R＝ ‎＝＝，‎ ‎∴S球＝4π·R2＝20π.‎ ‎(理)(2013·安徽六校教研会联考)四棱锥P－ABCD的五个顶点都在一个球面上，该四棱锥的三视图如图所示，E，F分别是棱AB，CD的中点，直线EF被球面截得的线段长为2，则该球的表面积为(　　)‎ A．9π B．3π C．2π D．12π ‎[答案]　D ‎[解析]　该几何体的直观图如图所示，‎ 该几何体可看作由正方体截得的，则正方体外接球的直径即为PC.由直线EF被球面所截得的线段长为2，可知正方形ABCD的对角线AC的长为2，可得a＝2，在△PAC中，PC＝＝2，‎ ‎∴球的半径R＝，∴S表＝4πR2＝4π×()2＝12π.‎ ‎6．(文)一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积为，那么这个三棱柱的体积是(　　)‎ A．96　　 B．48　　‎ C．24　　 D．16 ‎[答案]　B ‎[解析]　已知正三棱柱的高为球的直径，底面正三角形的内切圆等于球的大圆．设底面正三角形的边长为a，球的半径为R，则a＝2R，又πR3＝，∴R＝2，a＝4，于是V＝a2·2R＝48.‎ ‎(理)如图，在等腰梯形ABCD中，AB＝2DC＝2，∠DAB＝60°，E为AB的中点，将△ADE与△BEC分别沿ED、EC向上折起，使A、B重合于点P，则三棱锥P－DCE的外接球的体积为(　　)‎ A. B. C. D. ‎[答案]　C ‎[解析]　根据题意折叠后的三棱锥P－DCE为正四面体，且棱长为1，以此正四面体来构造正方体，则此正方体的棱长为，故正方体的体对角线的长为，且正方体的外接球也为此正四面体的外接球，∴外接球的半径为，‎ ‎∴V球＝πr3＝π3＝，选C.‎ 二、填空题 ‎7．若某几何体的三视图(单位：cm)如图所示，则此几何体的表面积是________cm3.‎ ‎[答案]　112＋24 ‎[解析]　由三视图知，该几何体是一个正四棱台和一个正四棱柱的组合体，四棱台下底面边长为8，上底面边长为4，高为3，故棱台的斜高h′＝＝.上面正四棱柱底面边长为4，高为2，则表面积为 S＝4×4＋4×(4×2)＋8×8＋4×[×(4＋8)×]＝112＋24(cm3)．‎ ‎8.‎ 如图所示，在△ABC中，∠C＝90°，∠A＝30°，BC＝1.在三角形内挖去半圆(圆心O在边AC上，半圆分别与BC、AB相切于点C、M，与AC交于点N)，则图中阴影部分绕直线AC旋转一周所得旋转体的体积为______．‎ ‎[答案]　 ‎[解析]　阴影部分绕AC旋转一周所得旋转体为圆锥中挖去一个球，圆锥的体积V＝π×12×＝π，球体积V1＝×3＝，‎ 故所求体积为－＝.‎ ‎9．侧棱长为2的正三棱锥V－ABC中，∠AVB＝∠BVC＝∠CVA＝40°，过点A作截面AEF，则截面△AEF周长的最小值为________．‎ ‎[答案]　6‎ ‎[解析]　沿侧棱VA剪开，侧面展开如图，线段AA1的长为所求△AEF周长的最小值，取AA1中点D，则VD⊥AA1，∠AVD＝60°，∴AA1＝2AD＝6.‎ 三、解答题 ‎10．(文)(2012·新课标全国文，19)如图，在三棱柱ABC－A1B‎1C1中，侧棱垂直于底面，∠‎ ACB＝90°，AC＝BC＝AA1，D是棱AA1的中点．‎ ‎(1)证明：平面BDC1⊥平面BDC；‎ ‎(2)平面BDC1分此棱柱为两部分，求这两部分体积的比．‎ ‎[分析]　(1)证两个平面垂直，可转化为在其中一个平面内找到一条直线与另一个平面垂直；‎ ‎(2)平面BDC1分棱柱成两部分，下面部分B－ADC‎1C为四棱锥，可直接求体积，上面部分可用间接法求得体积，从而确定两部分体积之比．‎ ‎[解析]　(1)证明：由题设知BC⊥CC1，BC⊥AC，CC1∩AC＝C，所以BC⊥平面ACC‎1A1.‎ 又DC1⊂平面ACC‎1A1，所以DC1⊥BC.‎ 由题设知∠A1DC1＝∠ADC＝45°，‎ 所以∠CDC1＝90°，即DC1⊥DC.‎ 又DC∩BC＝C，所以DC1⊥平面BDC.‎ 又DC1⊂平面BDC1，故平面BDC1⊥平面BDC.‎ ‎(2)设棱锥B－DACC1的体积为V1，AC＝1.‎ 由题意得，V1＝××1×1＝.‎ 又三棱柱ABC－A1B‎1C1的体积V＝1，所以(V－V1)V1＝11.‎ 故平面BDC1分此棱柱所得两部分体积的比为11.‎ ‎[点评]　本题考查线面的位置关系及几何体体积的求法．求解几何体的体积时，若遇不规则的几何体时，经常采用割补法和间接法求其体积．‎ ‎(理)如图，已知四棱锥P－ABCD中，底面ABCD是直角梯形，AB∥DC，∠ABC＝45°，DC＝1，AB＝2，PA⊥平面ABCD，PA＝1.‎ ‎(1)求证：AB∥平面PCD；‎ ‎(2)求证：BC⊥平面PAC；‎ ‎(3)若M是PC的中点，求三棱锥M－ACD的体积．‎ ‎[证明]　(1)由已知底面ABCD是直角梯形，AB∥DC，‎ 又AB⊄平面PCD，CD⊂平面PCD，‎ ‎∴AB∥平面PCD.‎ ‎(2)在直角梯形ABCD中，过C作CE⊥AB于点E，则四边形ADCE为矩形，‎ ‎∴AE＝DC＝1‎ 又AB＝2，∴BE＝1，‎ 在Rt△BEC中，∠ABC＝45°，‎ ‎∴CE＝BE＝1，CB＝，∴AD＝CE＝1，‎ 则AC＝＝，AC2＋BC2＝AB2，‎ ‎∴BC⊥AC.‎ 又PA⊥平面ABCD，∴PA⊥BC，‎ 又PA∩AC＝A，∴BC⊥平面PAC.‎ ‎(3)∵M是PC中点，‎ ‎∴M到平面ADC的距离是P到平面ADC距离的一半．‎ ‎∴VM－ACD＝S△ACD·(PA)＝×(×1×1)×＝.‎ 能力拓展提升 一、选择题 ‎11．(2013·河北教学质量监测)已知正六棱柱的12个顶点都在一个半径为3的球面上，当正六棱柱的底面边长为时，其高的值为(　　)‎ A．3 B. C．2 D．2 ‎[答案]　D ‎[解析]　设正六棱柱的高为h，则可得()2＋＝32，解得h＝2.‎ ‎12．如图，正方体ABCD－A1B‎1C1D1的棱长为2.动点E、F在棱A1B1上，点Q是棱CD的中点，动点P在棱AD上．若EF＝1，DP＝x，A1E＝y(x，y大于零)，则三棱锥P－EFQ的体积(　　)‎ A．与x、y都有关 B．与x、y都无关 C．与x有关，与y无关 D．与y有关，与x无关 ‎[答案]　C ‎[解析]　设P到平面EFQ的距离为h，则VP－EFQ＝×S△EFQ·h，由于Q为CD的中点，∴点Q到直线EF的距离为定值，又EF＝1，∴S△EFQ为定值，而P点到平面EFQ的距离，即P点到平面A1B1CD的距离，显然与x有关与y无关，故选C.‎ ‎13．(2013·天津新华中学月考)如图是一个几何体的正视图、侧视图、俯视图，则该几何体的体积是(　　)‎ A．24 B．12‎ C．8 D．4‎ ‎[答案]　B ‎[解析]　由三视图可知，该几何体由两个相同的直三棱柱构成，三棱柱的高为4，三棱柱的底面为直角三角形，两直角边分别为2，，所以三棱柱的底面积为×2×＝，所以三棱柱的体积为×4＝6.即该几何体的体积为2×6＝12.故选B.‎ 二、填空题 ‎14．(2013·山西诊断)已知三棱锥P－ABC的各顶点均在一个半径为R的球面上，球心O在AB上，PO⊥平面ABC，＝，则三棱锥与球的体积之比为________．‎ ‎[答案]　 ‎[解析]　‎ 如图，依题意，AB＝2R，又＝，∠ACB＝90°，因此AC＝R，BC＝R，VP－ABC＝PO·S△ABC＝×R×(×R×R)＝R3.而V球＝R3，因此VP－ABCV球＝R3R3＝8π.‎ ‎15．(文)(2013·杭州二模)已知正三棱柱ABC－A′B′C′的正视图和侧视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，在旋转过程中对应的俯视图的面积为S，则S的最大值为________．‎ ‎[答案]　8‎ ‎[解析]　据正视图与侧视图知，该三棱柱的初始状态是水平放置的，直观图如图所示．‎ 据所给的数据知，底面正三角形的高是，∴底面边长是2.将三棱柱绕OO′旋转时，俯视图是矩形，该矩形的一组对边的长度保持不变(长度为4)，另一组对边长度不断变化，在底投影面上的投影的长度的最大值为2，∴S的最大值为4×2＝8.‎ ‎(理)已知在直三棱柱ABC－A1B‎1C1中，底面为直角三角形，∠ACB＝90°，AC＝6，BC＝CC1＝，P是BC1上一动点，如图所示，则CP＋PA1的最小值为________．‎ ‎[答案]　5 ‎[解析]　PA1在平面A1BC1内，PC在平面BCC1内，将其铺平后转化为平面上的问题解决．计算A1B＝AB1＝，BC1＝2，又A‎1C1＝6，故△A1BC1是∠A‎1C1B＝90°的直角三角形．铺平平面A1BC1、平面BCC1，如图所示．‎ CP＋PA1≥A‎1C.在△AC‎1C中，由余弦定理得，‎ A‎1C＝＝5，故(CP＋PA1)min＝5.‎ ‎[点评]　多面体或旋转体表面上两点的最短距离问题，一般选择恰当的棱或母线剪开展平，转化为平面上两点间线段最短问题解决．‎ 三、解答题 ‎16．(文)如图1，在直角梯形ABCD中，∠ADC＝90°，CD∥AB，AB＝4，AD＝CD＝2，将△ADC沿AC折起，使平面ADC⊥平面ABC，得到几何体D－ABC，如图2所示．‎ ‎(1)求证：BC⊥平面ACD；‎ ‎(2)求几何体D－ABC的体积．‎ ‎[解析]　(1)证明：由条件可得AC＝BC＝2，‎ 从而AC2＋BC2＝AB2，故AC⊥BC.‎ 又平面ADC⊥平面ABC，‎ 平面ADC∩平面ABC＝AC，‎ BC⊂平面ABC，∴BC⊥平面ACD.‎ ‎(2)由(1)可知BC为三棱锥B－ACD的高，BC＝2，S△ACD＝2，‎ ‎∴VB－ACD＝S△ACD·BC＝×2×2＝，‎ ‎∴几何体D－ABC的体积为.‎ ‎(理)(2013·新课标Ⅱ)如图，直三棱柱ABC－A1B‎1C1中，D，E分别是AB，BB1的中点．‎ ‎(1)证明：BC1∥平面A1CD；‎ ‎(2)设AA1＝AC＝CB＝2，AB＝2，求三棱锥C－A1DE的体积．‎ ‎[解析]　(1)证明：如图，连结AC1交A‎1C于点F，则F为AC1中点，又D是AB中点，连结DF，则BC1∥DF，‎ 因为DF⊂平面A1CD，BC1⊄平面A1CD，‎ 所以BC1∥平面A1CD.‎ ‎(2)因为ABC－A1B‎1C1是直三棱柱，所以AA1⊥CD.由已知AC＝CB，D为AB的中点，所以CD⊥AB.又AA1∩AB＝A，于是CD⊥平面ABB‎1A1.‎ 由AA1＝AC＝CB＝2，AB＝2得，‎ ‎∠ACB＝90°，CD＝，A1D＝，DE＝，A1E＝3，‎ 故A1D2＋DE2＝A1E2，即DE⊥A1D 所以VC－A1DE＝×(××)×＝1.‎ 考纲要求 了解球、柱、锥、台的表面积和体积的计算公式．‎ 补充说明 ‎1．棱锥的平行于底面的截面性质：棱锥被平行于底面的平面所截，截面与底面相似，相似比等于截得小棱锥与原棱锥的对应边(侧棱、高)的比．面积比等于相似比的平方，若棱锥为正棱锥，则两底面对应半径的比、对应边的比、对应边心距的比、斜高的比都等于相似比．‎ ‎2．空间几何体的表面积、侧面积计算一般都可以转化为平面图形的面积计算；将圆柱、圆锥、圆台的侧面展开是把立体几何问题转化为平面几何问题处理的重要手段之一；关于球的问题中的计算，常选取球的一个大圆，化“球”为“圆”，应用平面几何的有关知识解决．‎ ‎3．根据几何体的结构特征判断几何体的类型，首先应熟练掌握各类几何体的概念和性质，其次要有一定的空间想象能力．‎ ‎4．转化思想 立体几何处理问题的一个基本思想就是转化，包括复杂向简单转化，高维向低维降维转化等等，割补法、等积变换、卷、折、展都是转化思想在处理立体几何问题中的体现．‎ ‎(1)割补法 割补法是割法与补法的总称．补法是把不熟悉的(或复杂的)几何体延伸或补成熟悉的(或简单的)几何体，把不完整的图形补成完整的图形．割法是把复杂的几何体切割成简单的几何体．‎ ‎(2)等积变换 在求几何体的体积、高(点到面的距离)等问题时，常常要通过等积变换来处理，等积变换的主要依据有：‎ ‎①平行线间距离处处相等．‎ ‎②平行平面间的距离处处相等．‎ ‎③若l∥α，则l上任一点到平面α的距离都相等．‎ ‎④等底面积等高的柱(锥)体的体积相等，锥体的体积是等底面积等高的柱体体积的.‎ ‎⑤三棱锥A－BCD中，有VA－BCD＝VB－ACD＝VC－ABD＝VD－ABC.‎ ‎(3)卷起、展开与折叠 ‎①将平面图形卷成旋转体(或将旋转体侧面展开)、将平面图形折成多面体，要注意折(卷、展)前后几何量的对应关系和位置关系，弄清哪些量发生了什么变化，哪些量没有变化，特别注意其中的平行、垂直位置关系．‎ ‎②多面体或旋转体的表面距离最值问题，常通过展开图来解决．‎ ‎(4)对于某些简单几何体的组合体问题，常常通过作出截面，使构成组合体的各简单几何体的元素，相对地集中在一个平面图形中，以达到空间问题向平面问题的转化．‎ 备选习题 ‎1．已知S、A、B、C是球O表面上的点，SA⊥平面ABC，AB⊥BC，SA＝AB＝1，BC＝，则球O的表面积等于(　　)‎ A．4π　　　 B．3π　　　‎ C．2π　　　 D．π ‎[答案]　A ‎[解析]　‎ ‎∵AB⊥BC，∴AC为截面圆的直径，∴AC中点为截面圆的圆心．‎ 设D为AC中点，连OD，则OD⊥平面ABC，‎ ‎∵SA⊥平面ABC，‎ ‎∴SA∥OD.‎ 连SC，则SC＝＝＝2.‎ 又SB＝，BC＝，∵SC2＝SB2＋BC2，‎ ‎∴∠SBC＝90°，∵∠SAC＝90°，∴SC为球O的直径，‎ ‎∵2R＝2，故R＝1，∴S球＝4πR2＝4π，选A.‎ ‎2.‎ ‎(2013·东北三省四市诊断)如图所示是一个几何体的三视图，其侧视图是一个边长为a的等边三角形，俯视图是两个正三角形拼成的菱形，则该几何体的体积为(　　)‎ A．a3 B. C. D. ‎[答案]　D ‎[解析]　该几何体由两个全等的三棱锥组合而成的，三棱锥的底面是边长为a的等边三角形，一条侧棱与底面垂直，且这条与底面垂直的侧棱长为a，所以该几何体的体积为V＝2×(×a2×a)＝.‎ ‎3．(2013·辽宁五校联考)已知三边长分别为3、4、5的△ABC的外接圆恰好是球O的一个大圆，P为球面上一点，若点P到△ABC的三个顶点的距离相等，则三棱锥P－ABC的体积为(　　)‎ A．5 B．10‎ C．20 D．30‎ ‎[答案]　A ‎[解析]　由题意得三角形ABC为直角三角形，其外接圆的直径2R＝5，设P在平面ABC上的射影为G，∵P到三个顶点的距离相等，∴GA＝GB＝GC，∴G为△ABC的外心，∴G与球心O(即AB的中点)重合，∴OP⊥平面ABC，故所求的体积V＝S△ABC×R＝×(×3×4)×＝5.‎ ‎4．侧棱与底面垂直的棱柱称为直棱柱．已知直三棱柱ABC－A1B‎1C1的各顶点都在球O的球面上，且AB＝AC＝1，BC＝，若球O的体积为π，则这个直三棱柱的体积等于(　　)‎ A．1 B. C．2 D. ‎[答案]　D ‎[解析]　设球O的半径为R，则＝，∴R＝，设△ABC外接圆半径为r，BC边上的高为h，则h＝＝，(h－r)2＋()2＝r2，‎ ‎∴r＝1；设棱柱的高为H，则R2＝r2＋()2，‎ ‎∴H＝4，∴V棱柱＝×××4＝.‎