- 2021-05-13 发布 |
- 37.5 KB |
- 6页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届高考数学一轮复习 第7讲 二次函数与幂函数学案(无答案)文
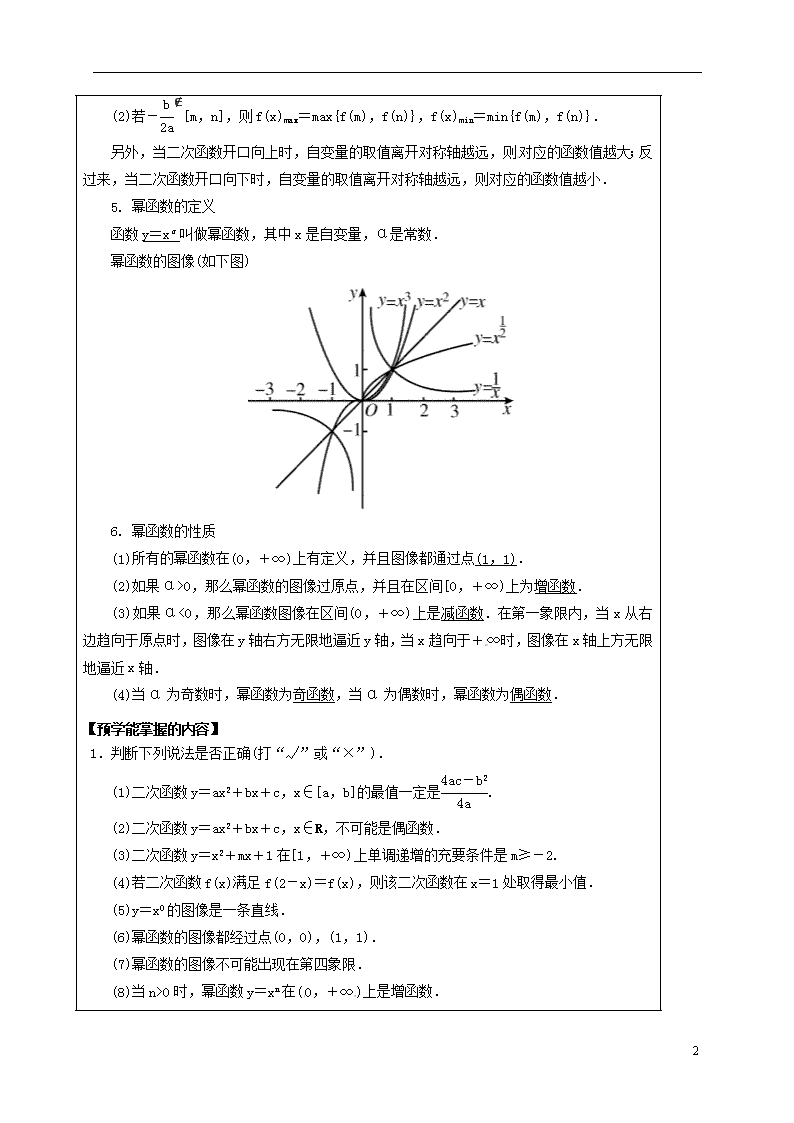
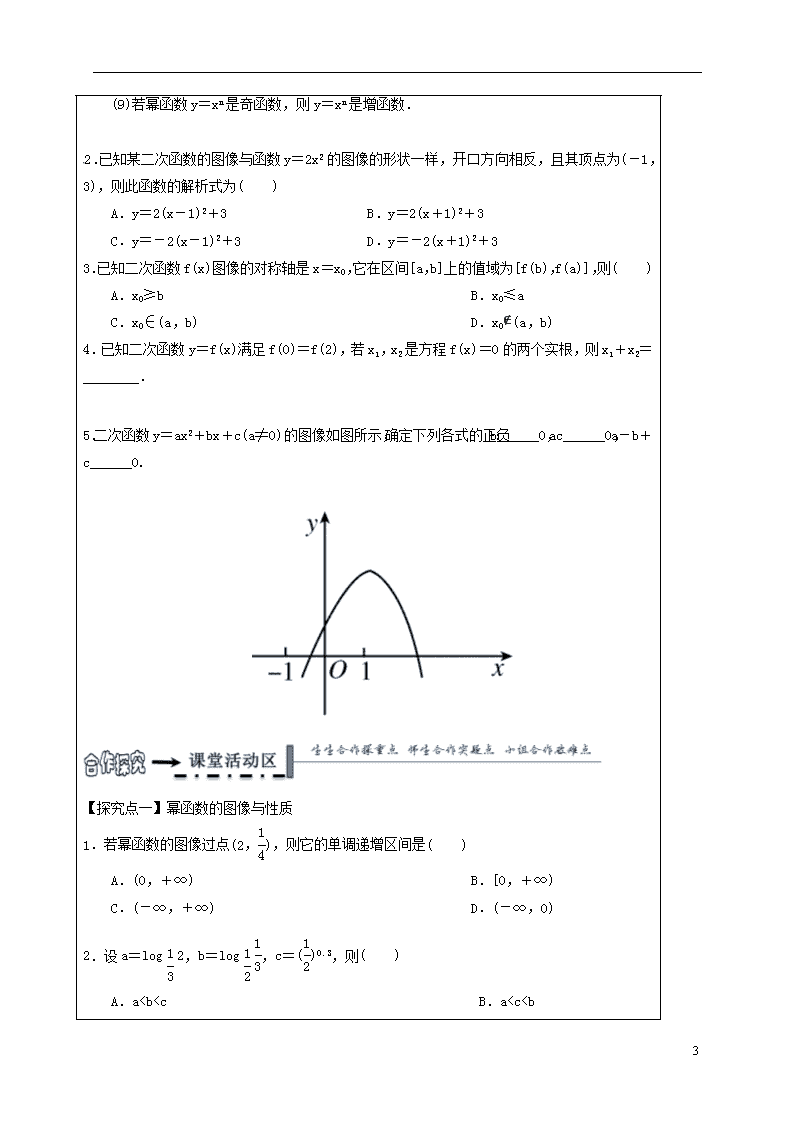
第七讲 二次函数与幂函数 学习 目标 1.理解并掌握二次函数的定义、图像及性质. 2.会求二次函数在闭区间上的最值. 3.能用二次函数、一元二次方程及一元二次不等式之间的联系去解决有关问题. 学习 疑问 学习 建议 【相关知识点回顾】 1.二次函数的解析式的三种形式 (1)一般式:y=ax2+bx+c(a≠0);对称轴方程是x=-;顶点为(-,). (2)两根式:y=a(x-x1)(x-x2);对称轴方程是x=;与x轴的交点为(x1,0),(x2,0). (3)顶点式:y=a(x-k)2+h;对称轴方程是x=k;顶点为(k,h) 2.二次函数的单调性 当a>0时,在(-,+∞)上为增函数;在(-∞,-)上为减函数;当a<0时,与之相反. 3.二次函数与一元二次方程、一元二次不等式之间的内在联系 (1)f(x)=ax2+bx+c(a≠0)的图像与x轴交点的横坐标是方程ax2+bx+c=0的实根. (2)若x1,x2为f(x)=0的实根,则f(x)在x轴上截得的线段长应为|x1-x2|=. (3)当时,恒有f(x)>0;当时,恒有f(x)<0. 4.设f(x)=ax2+bx+c(a>0),则二次函数在闭区间[m,n]上的最大、最小值的分布情况 (1)若-∈[m,n],则f(x)max=max,f(x)min=f(-). (2)若-∉[m,n],则f(x)max=max{f(m),f(n)},f(x)min=min{f(m),f(n)}. 6 另外,当二次函数开口向上时,自变量的取值离开对称轴越远,则对应的函数值越大;反过来,当二次函数开口向下时,自变量的取值离开对称轴越远,则对应的函数值越小. 5. 幂函数的定义 函数y=xα叫做幂函数,其中x是自变量,α是常数. 幂函数的图像(如下图) 6. 幂函数的性质 (1)所有的幂函数在(0,+∞)上有定义,并且图像都通过点(1,1). (2)如果α>0,那么幂函数的图像过原点,并且在区间[0,+∞)上为增函数. (3)如果α<0,那么幂函数图像在区间(0,+∞)上是减函数.在第一象限内,当x从右边趋向于原点时,图像在y轴右方无限地逼近y轴,当x趋向于+∞时,图像在x轴上方无限地逼近x轴. (4)当α为奇数时,幂函数为奇函数,当α为偶数时,幂函数为偶函数. 【预学能掌握的内容】 1.判断下列说法是否正确(打“√”或“×”). (1)二次函数y=ax2+bx+c,x∈[a,b]的最值一定是. (2)二次函数y=ax2+bx+c,x∈R,不可能是偶函数. (3)二次函数y=x2+mx+1在[1,+∞)上单调递增的充要条件是m≥-2. (4)若二次函数f(x)满足f(2-x)=f(x),则该二次函数在x=1处取得最小值. (5)y=x0的图像是一条直线. (6)幂函数的图像都经过点(0,0),(1,1). (7)幂函数的图像不可能出现在第四象限. (8)当n>0时,幂函数y=xn在(0,+∞)上是增函数. (9)若幂函数y=xn是奇函数,则y=xn是增函数. 6 2.已知某二次函数的图像与函数y=2x2的图像的形状一样,开口方向相反,且其顶点为(-1,3),则此函数的解析式为( ) A.y=2(x-1)2+3 B.y=2(x+1)2+3 C.y=-2(x-1)2+3 D.y=-2(x+1)2+3 3.已知二次函数f(x)图像的对称轴是x=x0,它在区间[a,b]上的值域为[f(b),f(a)],则( ) A.x0≥b B.x0≤a C.x0∈(a,b) D.x0∉(a,b) 4.已知二次函数y=f(x)满足f(0)=f(2),若x1,x2是方程f(x)=0的两个实根,则x1+x2=________. 5.二次函数y=ax2+bx+c(a≠0)的图像如图所示,确定下列各式的正负:b______0,ac______0,a-b+c______0. 【探究点一】幂函数的图像与性质 1.若幂函数的图像过点(2,),则它的单调递增区间是( ) A.(0,+∞) B.[0,+∞) C.(-∞,+∞) D.(-∞,0) 2.设a=log2,b=log,c=()0.3,则( ) A.a查看更多
相关文章
- 当前文档收益归属上传用户