2018中考相似三角形动点问题分类讨论问题培优及答案

2018中考相似三角形动点问题分类讨论问题培优及答案

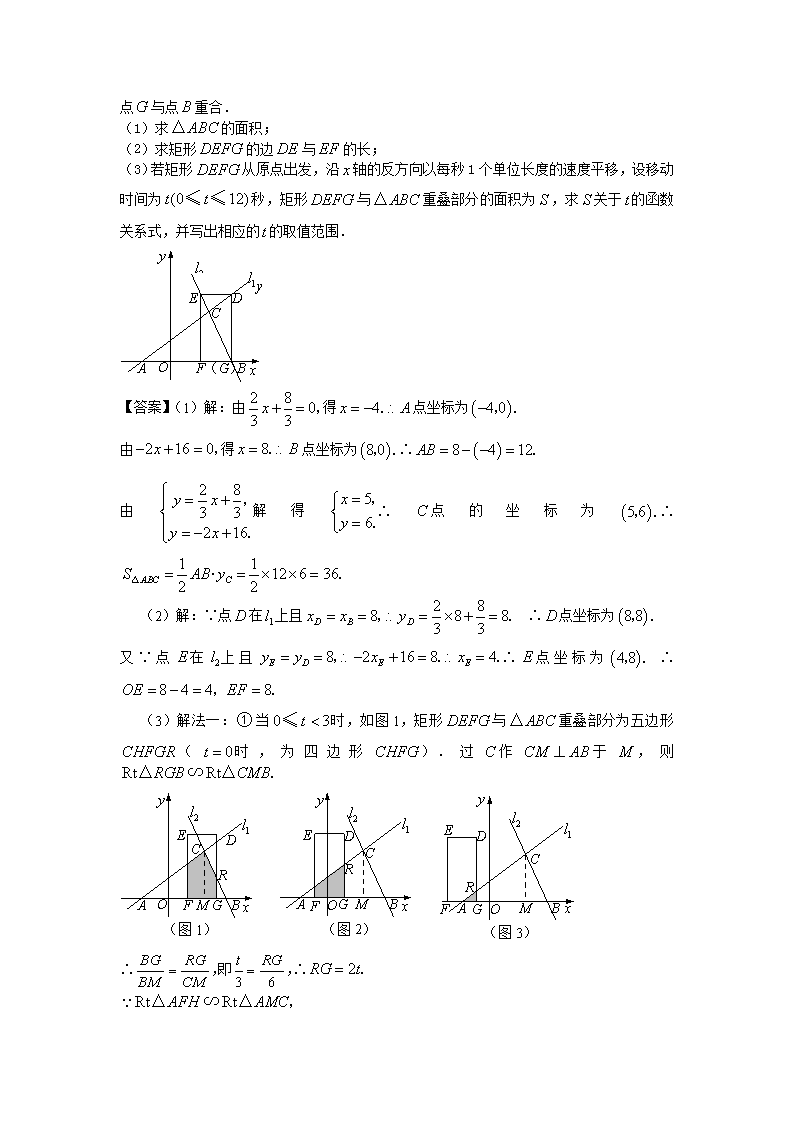
‎2018年中考复习 相似 动点 分类讨论 ‎1.如图，已知一个三角形纸片，边的长为8，边上的高为，和都为锐角，为一动点（点与点不重合），过点作，交于点，在中，设的长为，上的高为．‎ ‎（1）请你用含的代数式表示．‎ ‎（2）将沿折叠，使落在四边形所在平面，设点落在平面的点为，与四边形重叠部分的面积为，当为何值时，最大，最大值为多少？‎ ‎【答案】解：（1）‎ ‎（2）的边上的高为，‎ 当点落在四边形内或边上时，=（0）‎ 当落在四边形外时，如下图，‎ 设的边上的高为，则 ‎ ‎ ‎ ‎ 所 M N C B E F A A1‎ 综上所述：当时，，取，‎ 当时，，取，‎ 当时，最大，‎ ‎2．如图，抛物线经过三点．‎ ‎（1）求出抛物线的解析式；‎ ‎（2）P是抛物线上一动点，过P作轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；‎ ‎【答案】解：（1）该抛物线过点，可设该抛物线的解析式为．‎ 将，代入，‎ 得解得此抛物线的解析式为．‎ ‎（2）存在．‎ 如图，设点的横坐标为，则点的纵坐标为，‎ 当时，，．‎ 又，①当时，，‎ 即．解得（舍去），．‎ ‎②当时，，即．‎ 解得，（均不合题意，舍去）当时，．‎ 类似地可求出当时，．‎ 当时，．综上所述，符合条件的点为或或．‎ ‎3．如图，已知直线与直线相交于点分别交轴于两点．矩形的顶点分别在直线上，顶点都在 轴上，且点与点重合．‎ ‎（1）求的面积；‎ ‎（2）求矩形的边与的长；‎ ‎（3）若矩形从原点出发，沿轴的反方向以每秒1个单位长度的速度平移，设移动时间为秒，矩形与重叠部分的面积为，求关于的函数关系式，并写出相应的的取值范围．‎ A D B E O C F x y y ‎（G）‎ ‎【答案】（1）解：由得点坐标为 由得点坐标为∴‎ 由解得∴点的坐标为∴‎ ‎ （2）解：∵点在上且 ∴点坐标为 又∵点在上且∴点坐标为 ∴‎ ‎ （3）解法一：当时，如图1，矩形与重叠部分为五边形（时，为四边形）．过作于，则 A D B E O R F x y y M ‎（图3）‎ G C A D B E O C F x y y G ‎（图1）‎ R M A D B E O C F x y y G ‎（图2）‎ R M ‎∴即∴‎ ‎∴即 ‎ 当时，如图2，为梯形面积，∵G（8－t,0）∴GR=,‎ ‎∴‎ 当时，如图3,为三角形面积，‎ ‎4．如图，矩形中，厘米，厘米（）．动点同时从点出发，分别沿，运动，速度是厘米／秒．过作直线垂直于，分别交，于．当点到达终点时，点也随之停止运动．设运动时间为秒．‎ ‎（1）若厘米，秒，则______厘米；‎ ‎（2）若厘米，求时间，使，并求出它们的相似比；‎ ‎（3）若在运动过程中，存在某时刻使梯形与梯形的面积相等，求的取值范围；‎ D Q C P N B M A D Q C P N B M A ‎（4）是否存在这样的矩形：在运动过程中，存在某时刻使梯形，梯形，梯形的面积都相等？若存在，求的值；若不存在，请说明理由．‎ ‎ ‎ ‎【答案】解： （1），‎ ‎（2），使，相似比为 ‎（3），‎ ‎，即，‎ 当梯形与梯形的面积相等，即 化简得，‎ ‎，，则，‎ ‎（4）时梯形与梯形的面积相等 梯形的面积与梯形的面积相等即可，则 ‎，把代入，解之得，所以．‎ 所以，存在，当时梯形与梯形的面积、梯形的面积相等．‎ ‎5．如图，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），解答下列问题：‎ ‎（1）当t＝2时，判断△BPQ的形状，并说明理由；‎ ‎（2）设△BPQ的面积为S（cm2），求S与t的函数关系式；‎ ‎（3）作QR//BA交AC于点R，连结PR，当t为何值时，△APR∽△PRQ？‎ ‎【答案】 解：(1)△BPQ是等边三角形,当t=2时,AP=2×1=2,BQ=2×2=4,所以BP=AB-AP=6-2=4,所以BQ=BP.又因为∠B=600,所以△BPQ是等边三角形.‎ ‎(2)过Q作QE⊥AB,垂足为E,由QB=2y,得QE=2t·sin600=t,由AP=t,得PB=6-t,‎ 所以S△BPQ=×BP×QE=(6-t)×t=－t2+3t；‎ ‎(3)因为QR∥BA,所以∠QRC=∠A=600，∠RQC=∠B=600，又因为∠C=600,‎ 所以△QRC是等边三角形,所以QR=RC=QC=6-2t.因为BE=BQ·cos600=×2t=t,‎ 所以EP=AB-AP-BE=6-t-t=6-2t,所以EP∥QR,EP=QR,所以四边形EPRQ是平行四边形,‎ 所以PR=EQ=t,又因为∠PEQ=900,所以∠APR=∠PRQ=900.因为△APR～△PRQ,‎ 所以∠QPR=∠A=600,所以tan600=,即,所以t=,所以当t=时, △APR～△PRQ ‎ ‎ ‎6．在直角梯形OABC中，CB∥OA，∠COA＝90º，CB＝3，OA＝6，BA＝3．分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系．‎ ‎（1）求点B的坐标；‎ ‎（2）已知D、E分别为线段OC、OB上的点，OD＝5，OE＝2EB，直线DE交x轴于点F．求直线DE的解析式；‎ ‎（3）点M是（2）中直线DE上的一个动点，在x轴上方的平面内是否存在另一个点N．使以O、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．‎ ‎ ‎ A B D E ‎（第26题 图1）‎ F C O M N x y 图7-2‎ A D O B C ‎2‎ ‎1‎ M N 图7-1‎ A D B M N ‎1‎ ‎2‎ 图7-3‎ A D O B C ‎2‎ ‎1‎ M N O ‎.7．在图15-1至图15-3中，直线MN与线段AB相交于点O，∠1 = ∠2 = 45°．‎ ‎（1）如图15-1，若AO = OB，请写出AO与BD 的数量关系和位置关系；‎ 图4‎ A D O B C ‎2‎ ‎1‎ M N E F ‎（2）将图15-1中的MN绕点O顺时针旋转得到图15-2，其中AO = OB．‎ 求证：AC = BD，AC ⊥ BD；‎ ‎（3）将图15-2中的OB拉长为AO的k倍得到 图15-3，求的值．‎ ‎【答案】 解：（1）AO = BD，AO⊥BD； ‎ ‎（2）证明：如图4，过点B作BE∥CA交DO于E，∴∠ACO = ∠BEO．‎ ‎  又∵AO = OB，∠AOC = ∠BOE，∴△AOC ≌ △BOE．∴AC = BE． ‎ 又∵∠1 = 45°， ∴∠ACO = ∠BEO = 135°．∴∠DEB = 45°．‎ ‎∵∠2 = 45°，∴BE = BD，∠EBD = 90°．∴AC = BD． 延长AC交DB的延长线于F，‎ A O B C ‎1‎ D ‎2‎ 图5‎ M N E 如图4．∵BE∥AC，∴∠AFD = 90°．∴AC⊥BD．‎ ‎（3）如图5，过点B作BE∥CA交DO于E，∴∠BEO = ∠ACO．‎ 又∵∠BOE = ∠AOC ， ∴△BOE ∽ △AOC．∴． ‎ 又∵OB = kAO，由（2）的方法易得 BE = BD．∴． ‎ ‎10．如图，已知过A（2，4）分别作x轴、y轴的垂线，垂足分别为M、N，若点P从O点出发，沿OM作匀速运动，1分钟可到达M点，点Q从M点出发，沿MA作匀速运动，1分钟可到达A点。‎ ‎（1）经过多少时间，线段PQ的长度为2？‎ ‎（2）写出线段PQ长度的平方y与时间t之间的函数关系式和t的取值范围；‎ ‎（3）在P、Q运动过程中，是否可能出现PQ⊥MN？若有可能，求出此时间t；若不可能，请说明理由；‎ ‎（4）是否存在时间t，使P、Q、M构成的三角形与△MON相似？若存在，求出此时间t；若不可能，请说明理由；‎ ‎ Y ‎ N A ‎ Q ‎ O P M X ‎ ‎ 考点五：相似三角形中的动点问题 ‎1．在矩形ABCD中，AB=12cm，AD=6cm，点P沿AB边从点A开始向点B以2cm/秒的速度移动，点Q沿DA边从点D开始向点A以1cm/秒的速度移动，如果P、Q同时出发，用t（秒）表示运动时间（0≤t≤6），那么当t为何值时，△APQ与△ABD相似？说明理由．‎ ‎ ‎ ‎2．（2011•乌鲁木齐）如图，在△ABC中，∠B=90°，AB=6米，BC=8米，动点P以2米/秒的速度从A点出发，沿AC向点C移动．同时，动点Q以1米/秒的速度从C点出发，沿CB向点B移动．当其中有一点到达终点时，它们都停止移动．设移动的时间为t秒．‎ ‎（1）①当t=2.5秒时，求△CPQ的面积；‎ ‎②求△CPQ的面积S（平方米）关于时间t（秒）的函数解析式；‎ ‎（2）在P，Q移动的过程中，当△CPQ为等腰三角形时，写出t的值；‎ ‎　‎ ‎　3．（ 金华）如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从A点出发，沿着AB以每秒4cm的速度向B点运动；同时点Q从C点出发，沿CA以每秒3cm的速度向A点运动，设运动时间为x．‎ ‎（1）当x为何值时，PQ∥BC；‎ ‎（2）当，求的值；‎ ‎（3）△APQ能否与△CQB相似？若能，求出AP的长；若不能，请说明理由．‎ ‎　‎ ‎　‎ ‎4．如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标为（6，0），（6，8）．动点M、N分别从O、B同时出发，都以每秒1个单位的速度运动，其中，点M沿OA向终点A运动，点N沿BC向终点C运动，过点N作NP⊥BC，交AC于点P，连接MP，已知动点运动了x秒．‎ ‎（1）用含x的代数式表示P的坐标（直接写出答案）；‎ ‎（2）设y=S四边形OMPC，求y的最小值，并求此时x的值；‎ ‎（3）是否存在x的值，使以P、A、M为顶点的三角形与△AOC相似？若存在，请求出x的值；若不存在，请说明理由．‎ ‎　‎ ‎5、如图，正方形的边长为，是边的中点，点在射线上，过作于．‎ ‎（1）求证：；‎ ‎（2）当点在射线上运动时，设，是否存在实数，使以为顶点的三角形也与相似？若存在，请求出的值；若不存在，说明理由．‎ ‎6．（2012•鸡西）如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2﹣7x+12=0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点0运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．‎ ‎（1）求A、B两点的坐标．‎ ‎（2）求当t为何值时，△APQ与△AOB相似.‎ ‎（3）当t=2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．‎