六年级数学教案 《式与方程》

六年级数学教案 《式与方程》

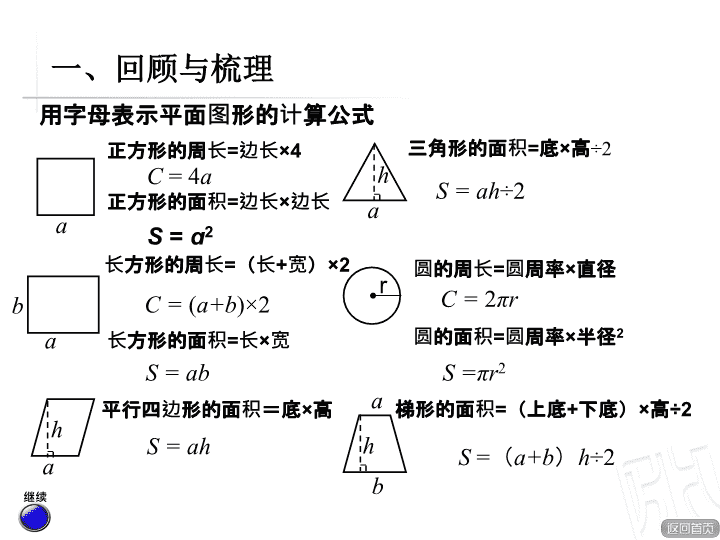
式与方程 总结与评价 回顾与梳理 应用与反思 讨论与交流 一、回顾与梳理 用字母表示数，可以简明地表达数量关系、运算律和计算公式。你能举出一些这样的例子吗？ 数量关系 计算公式 运算律 s=vt c=an 用字母表示数 S=ah a+b=b+a 继续 路程 = 速度 × 时间 平行四边形的面积 = 底 × 高 加法交换律 总价 = 单价 × 数量 长方形的面积 = 长 × 宽 长方形的周长 = （长 + 宽） ×2 用字母表示平面图形的计算公式 ɑ b S = ɑb C = ( ɑ+b )×2 h h S = ɑh ÷2 h ɑ b r C = 2 π r 继续 正方形的周长 = 边长 ×4 正方形的面积 = 边长 × 边长 C = 4 ɑ S = ɑ 2 圆的面积 = 圆周率 × 半径 2 圆的周长 = 圆周率 × 直径 S = π r 2 平行四边形的面积＝底 × 高 梯形的面积 = （上底 + 下底） × 高 ÷2 S = （ ɑ+b ） h ÷2 三角形的面积 = 底 × 高 ÷2 S = ɑh ɑ ɑ ɑ 一、回顾与梳理 用字母表示立体图形的计算公式 ɑ S = 6 ɑ 2 V = ɑ 3 ɑ b h S h S h S = （ ɑb+bh+ɑh ） ×2 V = Sh V= Sh 1 3 返回 正方体的表面积 = 棱长 × 棱长 ×6 正方体的体积 = 棱长 × 棱长 × 棱长 圆柱体的体积 = 底面积 × 高 长方体的体积 = 长 × 宽 × 高 长方体的表面积 =6 个面面积之和 V = abh 圆锥体的体积 = × 底面积 × 高 1 3 一、回顾与梳理 用字母表示运算律 两个加数 ɑ 、 b 相加，交换加数的位置，和不变。 三个数 ɑ 、 b 、 c 相加，先把前两个数相加， 或者先把后两个数相加 , 和不变。 两个因数 ɑ 、 b 相乘，交换因数的位置，积不变。 ɑ + b = b + ɑ ɑ b = b ɑ ɑ + ( b + c ) = ( ɑ + b )+ c 加法交换律： 加法结合律： 乘法交换律： 一、回顾与梳理 三个数 ɑ 、 b 、 c 相乘，先把前两个数相乘，再 和另外一个数相乘，或先把后两个数相乘，再 和另外一个数相乘，积不变。 两个数 ɑ 、 b 的和同一个数 c 相乘，等于把两个 加数分别同这个数相乘 , 再把两个积相加，结果 不变。 用字母表示运算律 ɑ （ bc ） = （ ɑb ） c 乘法结合律： 乘法分配律： ɑ （ b+c ） = ɑ b+ ɑ c 返回 一、回顾与梳理 简写时应注意什么呢？ 1. 在含有字母的式子里，数和字母中间的乘号可以用 “ • ”代替 ，也可以省略不写。 2. 省略乘号时，应当把数写在字母的前面。 3. 数与数之间的乘号不能省略。加号、减号、除号都不能省略。 一、回顾与梳理 试一试 1. 李奶奶家本月用电 a 千瓦时，比上个月多用 3 千瓦时，上个月用电（ ）千瓦时 。 2. 如果每千瓦时电的价格是 c 元，李奶奶家本月的电费是（ ）元。李奶奶家银行缴费卡上原有 215 元，扣除本月电费后，还剩（ ）元。 ɑ- 3 ɑ c 215- ɑc 你能把有关方程的知识整理一下吗？ 方程 方程的意义： 方程与等式的关系： 解方程： 含有未知数的等式叫作方程。 方程 等式 求方程解的过程叫作解方程。 一、回顾与梳理 试一试 1. 下列式子中，是方程的有哪些？为什么？ （ 1 ） 5 （ x -2.8 ） =140 （ 2 ） 20-5=15   （ 3 ） a +24 （ 4 ） （ 5 ） 3( x +2)>42 （ 6 ） 18<16+14 √ × 不是等式。 不含未知数也不是等式。 不含未知数。 × 不是等式。 × × x 2 = 33 √ 试一试 2. 解方程 3.5 χ -2 χ = 33 6 χ +2 = 26 解： 1.5 χ = 33 6 χ +2-2 = 26-2 1.5 χ ÷1.5 = 33÷1.5 6 χ = 24 χ = 22 χ = 4 解： 解方程的依据是什么？你能说说什么是等式的性质吗？ 等式的两边同时加、减、乘或除以同一个数，等式仍然成立，这是等式的性质。 某汽车制造厂去年 的 销售收入 为 8.4 亿元，比前年增长了 40 ％。前年的销售收入是多少亿元？ 解：设前年的销售收入为 χ 亿元。 （ 1+40% ） χ = 8.4 1.4 χ = 8.4 1.4 χ ÷1.4 = 8.4÷1.4 χ = 6 答：前年的销售收入是 6 亿元。 1 ．审题，理解题意； 你能说说用方程解决问题的步骤吗？ 2 ．找出等量关系； 3 ．根据等量关系列方程； 4 ．解方程； 5 ．检验写答句。 列方程解决问题。 一、回顾与梳理 试一试 说出下列各题中数量之间的等量关系。 1. 单价、数量、总价 2. 速度、时间、路程 3. 五年级一班男生和女生一共有 45 人。 4. 跳绳人数是打篮球人数的 3 倍。 5. 红花比黄花多 10 朵。 6. 书包的价格比钢笔的 3.5 倍还多 15 元。 单价 × 数量 = 总价 速度 × 时间 = 路程 男生人数 + 女生人数 =45 打篮球人数 ×3= 跳绳人数 黄花朵数 +10= 红花朵数 钢笔的价格 ×3.5+15= 书包的价格 二、讨论与交流 ● 用字母表示数有哪些优越性？ 观察下列图形并填表。你有什么发现？ 图 形 三角形 四边形 五边形 六边形 … n 边形 边 数 分成的三角形个数 内角和 3 4 n 5 6 … 1 2 3 4 n -2 … 360° 540 ° 720° ( n -2)×180° 180° … 用字母表示数更有利于表达和思考数学问题，使我们 的思维更抽象、更概括。 ● 用方程解决问题与算术法解决问题相比，有什么特点？ 二、讨论与交流 用方程解决问题 时，是把未知数当作已知数来思考 ， 将逆向思维变成顺向思维， 使较复杂的思考过程变得简单。 一台数码摄像机的价格是 8800 元，比一台数码照相机的价格的 3 倍少 200 元。一台数码照相机的价格是多少元？ （ 8800+200 ） ÷3 =9000÷3 =3000 （元） 解：设一台数码照相机的价格是 x 元。 3 x -200=8800 3 x -200+200=8800+200 3 x =9000 x =3000 （ 2 ）练习本每本 a 元，买 6 本要用 ( ) 元。 （ 3 ）一种贺卡的单价是 a 元，小英买了 5 张这样的贺卡，用去（ ）元；小明买 n 张这样的贺卡，付出 10 元，应找回 （ ）元。 10- an 6 a 三、应用与反思 1. 用含有字母的式子表示下面的数量关系。 （ 1 ）学校去年植树 a 棵，今年比去年多栽 6 棵。今年植树 ( ) 棵。 a +6 5 a 三、应用与反思 2. 解下列方程。 2 χ +9=27 8+0.3 χ = 14 解 : 解 : 2 χ +9-9 = 27-9 2 χ = 18 2 χ ÷2 = 18÷2 χ = 9 8+0.3 χ -8 = 14-8 0.3 χ = 6 0.3 χ ÷0.3 = 6÷0.3 χ = 20 三、应用与反思 2. 解下列方程。 8 χ - 3×9 = 37 22.3 χ +11 χ =66.6 解 : 8 χ -27 = 37 8 χ -27+27 = 37+27 8 χ = 64 8 χ ÷8 = 64÷8 χ = 8 33.3 χ = 66.6 解 : χ = 2 三、应用与反思 3. 王亮喜欢收藏玩具车。他收藏的玩具卡车有 18 辆，占总数的 。他一共收藏了多少辆玩具车？ 解：设王亮一共收藏了 χ 辆玩具车。 χ = 45 答：他一共收藏了 45 辆玩具车。 2 5 χ = 18 2 5 三、应用与反思 4 . 小明爸爸上月的手机话费是 68 元，比妈妈的手机话费少 66% 。妈妈上月的手机话费是多少？ 解：设妈妈上月的手机话费是 χ 元。 （ 1-66% ） χ = 68 χ = 200 答：妈妈上月的手机费是 200 元。 宝剑锋从磨砺出， 梅花香自苦寒来