苏教版数学六年级上册 第一单元测试卷1（含答案）

苏教版数学六年级上册 第一单元测试卷1（含答案）

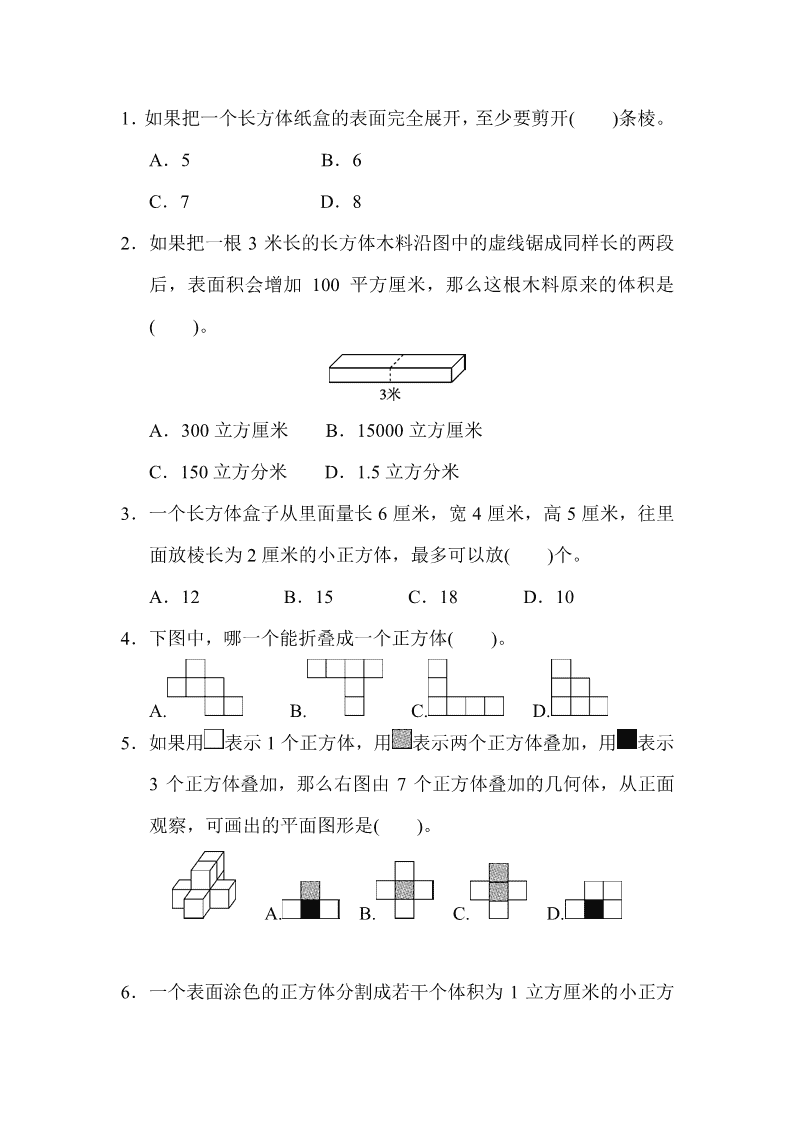
第一单元 检测卷 一、 填空。(每空 1 分，共 21 分) 1．在括号里填上合适的单位名称。 学校旗杆高 14.8( ) 一块橡皮的体积是 6.4( ) 一个游泳池蓄水约是 50( ) 一个热水瓶的容积是 2( ) 2．1270 立方厘米＝( )毫升＝( )升 0.42 立方分米＝( )立方厘米 3050 毫升＝( )升( )毫升 3.5 立方米＝( )立方分米 3．小新家有两块长 5 分米、宽 3 分米的玻璃，两块长 4 分米，宽 3 分米的玻璃，他爸爸想做一个长方体玻璃鱼缸，还要配一块长 ( )分米，宽( )分米的玻璃。 4．一个长方体，相交于一个顶点的 3 条棱的长度分别是 8 厘米，6 厘米，5 厘米。这个长方体的表面积是( )平方厘米，体积 是( )立方厘米。 5．用一根 48 厘米长的铁丝焊成一个体积最大的正方体模型，这个正 方体模型的体积是( )立方厘米。 6．把一个棱长 4 分米的正方体木料锯成 3 个相同的长方体，表面积 增加( )平方分米。 7．把一个长 124 厘米，宽 10 厘米，高 10 厘米的长方体锯成最大的 正方体，最多可锯成( )个。(每个正方体的大小相同) 8．把一个长 10 厘米，宽 8 厘米，高 6 厘米的长方体锯成两个小长方 体，表面积最少增加( )平方厘米，表面积最多增加( )平方 厘米。 9．用两个相同的正方体木块拼成一个长方体，长方体的表面积比两 个正方体的表面积的和少 16 平方厘米，其中一个正方体的表面积 是( )平方厘米。 10．小华观察一个模型(由棱长为 1 厘米的小正方体拼成)，分别从前 面、上面、右面观察，看到的图形如下图所示，那么该模型的体 积是( )立方厘米。 二、判断。(对的画“√”，错的画“×”)(每题 1 分，共 5 分) 1．长方体和正方体的表面积都可以用底面积乘高来计算。 ( ) 2．墨水瓶上有“净含量 60 毫升”的字样，这个 60 毫升是指墨水瓶的 容积。 ( ) 3．如果两个正方体的体积相等，那么它们的表面积也相等。( ) 4．如果长方体和正方体的底面积与高分别相等，那么它们的表面积 也相等。 ( ) 5．棱长 6 厘米的正方体表面积和体积相等。 ( ) 三、 选择。(将正确答案的字母填在括号里)(每题 1 分，共 6 分) 1．如果把一个长方体纸盒的表面完全展开，至少要剪开( )条棱。 A．5 B．6 C．7 D．8 2．如果把一根 3 米长的长方体木料沿图中的虚线锯成同样长的两段 后，表面积会增加 100 平方厘米，那么这根木料原来的体积是 ( )。 A．300 立方厘米 B．15000 立方厘米 C．150 立方分米 D．1.5 立方分米 3．一个长方体盒子从里面量长 6 厘米，宽 4 厘米，高 5 厘米，往里 面放棱长为 2 厘米的小正方体，最多可以放( )个。 A．12 B．15 C．18 D．10 4．下图中，哪一个能折叠成一个正方体( )。 A. B. C. D. 5．如果用 表示 1 个正方体，用 表示两个正方体叠加，用 表示 3 个正方体叠加，那么右图由 7 个正方体叠加的几何体，从正面 观察，可画出的平面图形是( )。 A. B. C. D. 6．一个表面涂色的正方体分割成若干个体积为 1 立方厘米的小正方 体，其中两面涂色的有 36 个，原来正方体的体积是( )立方厘 米。 A．64 B．125 C．216 D．27 四、 计算。(12 分) 1．下图是一个长方体纸盒的平面展开图，这个纸盒的体积是多少立 方厘米？(4 分) 2．求下面立体图形的表面积和体积。(单位：dm)(8 分) 五、 动手操作。(1 题 8 分，2 题 16 分，共 14 分) 1．一个长方体的长、宽都是 2 厘米，高是 3 厘米。 (1)请在下面方格图中把这个长方体的展开图画完整。(每个小方格的 面积是 1 平方厘米) (2)这个长方体的表面积是( )平方厘米，体积是( )立 方厘米。 2．将如图的长方形铁皮剪成 5 块，焊成一个底面是正方形的无盖长 方体容器，所焊容器的容积是多少？(分一分，再算一算) 六、解决问题。(5 题 8 分，6 题 6 分，其余每题 7 分，共 42 分) 1．一个长方体汽油箱，长和宽都是 6 dm，高是 5 dm。 (1)做这个汽油箱至少需要多少平方分米的铁皮？(铁皮厚度和接头处 忽略不计) (2)如果每升汽油的价格是 5.5 元，将这个空汽油箱加满汽油一共要付 多少元？ 2．一盒牛奶的外包装上标有“净含量 200 毫升”的字样，小明动手量 了一下，发现盒子从外面量长 5 cm，宽 4 cm，高 10 cm，你觉得 这个标注合适吗？为什么？ 3．把一根长 4 m 的长方体木料沿图中的虚线截成三段，表面积比原 来增加了 36 dm2，这根木料原来的体积是多少立方米？ 4．在一个长 25 cm，宽 12 cm，高 20 cm 的长方体玻璃缸中放入一个 棱长 9 厘米的正方体铁块，加水，使铁块完全浸没水中。当铁块 从水中取出时，玻璃缸中的水会下降多少厘米？ 5．我们知道要把一个长方体切成两个完全相同的小长方体，有三种 不同的切法，若这三种切法，增加出的表面积分别是 84 cm2， 70 cm2，60 cm2。 (1)你知道原来这个长方体的表面积吗？ (2)原来这个长方体的体积呢？ 6．用棱长为 1 cm 的小正方体按下面的规律摆长方体。 …… (1)用 3 个小正方体摆成的长方体表面积是 ( )cm2，体积是 ( )cm3。 (2)用 n 个小正方体摆成的长方体表面积是 ( )cm2，体积是 ( )cm3。 (3)用( )个小正方体摆成的长方体表面积是 22 cm2。 答案 一、1．米 立方厘米 立方米 升 2．1270 1.27 420 3 50 3500 3．5 4 4．236 240 5．64 6．64 7．12 8．96 160 9．48 10．5 二、1．× 2．× 3．√ 4．× 5．× 三、1．C 2．B 3．A 4．A 5．A 6．B 四、1．高：(28－10×2)÷2＝4(cm) 体积：4×10×6＝240(cm3) 2．S：8×8×6－4×4×2＝352(dm2) V：8×8×8－4×4×8＝384(dm3) 五、1．(1) (答案不唯一) (2)32 12 2． 20×20×5＝2000(dm3) 六、1．(1) 6×6×2＋6×5×4 ＝72＋120 ＝192(dm2) 答：做这个汽油箱至少需要 192 dm2 的铁皮。 (2)6×6×5×5.5＝990(元) 答：将这个空汽油箱加满汽油一共要付 990 元。 2．5×4×10＝200(cm3) 答：不合适，盒子有厚度。 3．36÷4＝9(dm2) 9 dm2＝0.09 m2 0.09×4＝0.36(m3) 答：这根木料原来的体积是 0.36 m3。 4．(9×9×9)÷(25×12)＝2.43(cm) 答：玻璃缸中的水会下降 2.43 cm。 5．(1)84＋70＋60＝214(cm2) 答：原来这个长方体的表面积是 214 cm2。 (2)84÷2＝42(cm2) 70÷2＝35(cm2) 60÷2＝30(cm2) 42＝6×7 35＝5×7 30＝6×5 5×6×7＝210(cm3) 答：原来这个长方体的体积是 210 cm3。 6．(1)14 3 (2)4n＋2 n (3)5