- 2021-11-11 发布 |
- 37.5 KB |
- 36页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江西专版2020中考数学复习方案第二单元方程组与不等式组第08课时一元二次方程及其应用课件
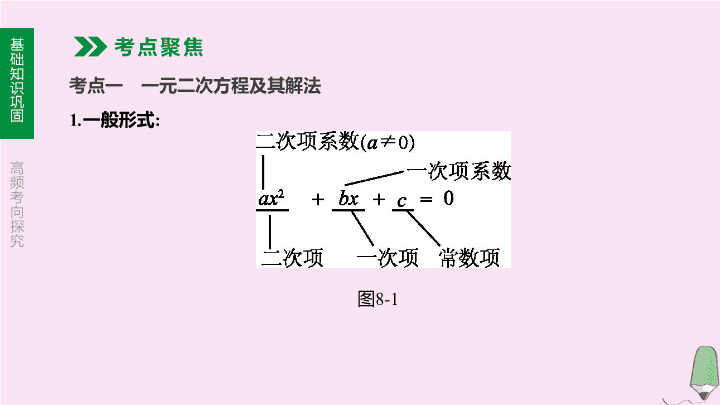
第 8 课时 一元二次方程及其应用 第二单元 方程(组)与不等式(组) 【考情分析】 高频考点 年份、题号、分值 题型 2020年中考预测 一元二次方程根与 系数的关系 2019、9、3分 填空题 ★★★★★ 2018、11、3分 填空题 2017、5、3分 选择题 2016、5、3分 选择题 2015、11、3分 填空题 2014、10、3分 填空题 基 础 知 识 巩 固 高 频 考 向 探 究 1.一般形式: 考点一 一元二次方程及其解法 考点聚焦 图8-1 基 础 知 识 巩 固 高 频 考 向 探 究 2.一元二次方程的解法 基 础 知 识 巩 固 高 频 考 向 探 究 (续表) 基 础 知 识 巩 固 高 频 考 向 探 究 1.判别式与根的关系 (1)b2-4ac>0⇔方程有④ 的实数根; (2)b2-4ac=0⇔方程有⑤ 的实数根; (3)b2-4ac<0⇔方程⑥ 实数根. 2.根与系数的关系 若关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1,x2, 则x1+x2=⑦ ,x1x2=⑧ . 考点二 一元二次方程根的判别式、根与系数的关系 两个不相等 两个相等 没有 基 础 知 识 巩 固 高 频 考 向 探 究 考点三 一元二次方程的实际应用 应用类型 等量关系 增长率问题 (1)增长率=增量÷基础量; (2)设a为原来的量,m为平均增长率,n为增长次数,b为增长后的量,则 a(1+m)n=b 销售利润问题 (1)纯利润=售出价-进货价-其他费用; (2)利润率=利润÷进货价×100%; (3)总利润=(售价-成本)×数量 基 础 知 识 巩 固 高 频 考 向 探 究 (a-2x)(b-2x) (a-x)(b-x) (续表) 基 础 知 识 巩 固 高 频 考 向 探 究 1.若关于x的方程(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是 ( ) A.m≠1 B.m=1 C.m≥1 D.m≠0 2.方程(x-2)(x+3)=0的解是 ( ) A.x=2 B.x=-3 C.x1=-2,x2=3 D.x1=2,x2=-3 题组一 必会题 对点演练 A D 基 础 知 识 巩 固 高 频 考 向 探 究 3.[2019·滨州]用配方法解一元二次方程x2-4x+1=0时,下列变形正确的是( ) A.(x-2)2=1 B.(x-2)2=5 C.(x+2)2=3 D.(x-2)2=3 4.[2019·泰州]方程2x2+6x-1=0的两根为x1,x2则x1+x2等于 ( ) A.-6 B.6 C.-3 D.3 D C 基 础 知 识 巩 固 高 频 考 向 探 究 5.关于x的一元二次方程x2-4x+m=0有实数根, 则实数m的取值范围是 ( ) A.m<4 B.m≥4 C.m≤4 D.m>4 [答案] C [解析]∵方程有实数根, ∴Δ=(-4)2-4×1·m=16-4m≥0, 解得m≤4.故选C. 基 础 知 识 巩 固 高 频 考 向 探 究 6.[2019·衡阳]国家实施“精准扶贫”政策以来,很多贫困人口走向了致富的道路, 某地区2016年底有贫困人口9万人,通过社会各界的努力,2018年底贫困人口减 少至1万人.设2016年底至2018年底该地区贫困人口的年平均下降率为x,根据题 意列方程得 ( ) A.9(1-2x)=1 B.9(1-x)2=1 C.9(1+2x)=1 D.9(1+x)2=1 B 基 础 知 识 巩 固 高 频 考 向 探 究 7.一元二次方程x2=3x的解是 . 题组二 易错题 【失分点】 忽略一元二次方程二次项系数不能为0的条件;解一元二次方程时,方程的两边直 接除以相同的整式,造成漏解;错用求根公式. x1=0,x2=3 8.[2019·枣庄]已知关于x的方程ax2+2x-3=0有两个不相等的实数根,则a的取值范 围是 . 基 础 知 识 巩 固 高 频 考 向 探 究 考向一 一元二次方程的解法 解:(1)(x+1)2=(1-2x)2. 直接开方得x+1=1-2x或x+1=-(1-2x), 解得x1=2,x2=0. 基 础 知 识 巩 固 高 频 考 向 探 究 (2)x2-6x+8=0. 因式分解得(x-2)(x-4)=0,可得x-2=0或x-4=0, 解得x1=2,x2=4. 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 【方法点析】配方法、公式法适合解所有的方程;直接开平方法适合解方程的 左边是完全平方式,右边是非负数的方程;因式分解法适合解左边能分解因式, 右边是0的方程.一般优先考虑使用直接开平方法和因式分解法,然后考虑使用 公式法解方程. 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 1.[2019·齐齐哈尔]解方程:x2+6x=-7. 基 础 知 识 巩 固 高 频 考 向 探 究 解:x(x-2)-(x-2)=0, 分解因式得(x-2)(x-1)=0, 即x-2=0或x-1=0, 解得x1=2,x2=1. 2.[2019·扬州改编]解方程:x(x-2)-(x-2)=0. 基 础 知 识 巩 固 高 频 考 向 探 究 考向二 运用一元二次方程根的判别式解题 [答案] D 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 1.判断一元二次方程x2-6x-7=0根的情况是 ( ) A.没有实数根 B.有两个不相等的实数根 C.有两个相等的实数根 D.无法确定 [答案] B [解析]因为Δ=(-6)2-4×(-7) = 64>0,所以有两个不相等的实 数根. 基 础 知 识 巩 固 高 频 考 向 探 究 2.[2018·威海] 关于x的一元二次方程 (m-5)x2+2x+2=0有实根,则m的最大整 数解是 . [答案] 4 [解析] ∵关于x的一元二次方程有实 数根,∴Δ=22-4(m-5)·2=4-8(m-5)≥0, 且m-5≠0,解得m≤5.5且m≠5,∴m的最 大整数解是4. 基 础 知 识 巩 固 高 频 考 向 探 究 考向三 运用一元二次方程根与系数的关系解题 例3[2015·江西11题]已知一元二次方程x2-4x-3=0的两根为m,n,则m2-mn+n2= . 25 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 1.[2016·江西5题]设α,β是一元二次方程 x2+2x-1=0的两个根,则αβ的值是( ) A.2 B.1 C.-2 D.-1 [答案] D 基 础 知 识 巩 固 高 频 考 向 探 究 [答案] D 基 础 知 识 巩 固 高 频 考 向 探 究 [答案] 0 [解析]∵x1,x2是一元二次方程x2-x-1=0 的两根, ∴x1+x2=1,x1x2=-1, ∴x1+x2+x1x2=1+(-1)=0. 3.[2019·江西9题]设x1,x2是一元二次方程 x2-x-1=0的两根,则x1+x2+x1x2= . 基 础 知 识 巩 固 高 频 考 向 探 究 4.[2014·江西10题]若α,β是方程x2-2x-3=0的两个根,则α2+β2= . 5.[2013·江西12题]若一个一元二次方程的两个根分别是Rt△ABC的两条直角边 长,且S△ABC=3,请写出一个符合题意的一元二次方程: . 10 x2-5x+6=0(答案不唯一) 基 础 知 识 巩 固 高 频 考 向 探 究 [答案] 2 基 础 知 识 巩 固 高 频 考 向 探 究 考向四 一元二次方程的应用 例4[2019·南京]某地计划对矩形广场进行扩建改造.如图8-2,原广场长50 m,宽40 m, 要求扩充后的矩形广场长与宽的比为3∶ 2.扩充区域的扩建费用为每平方米30元, 扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用为每平方米100元.如果计划 总费用为642000元,扩充后广场的长和宽应分别是多少米? 图8-2 基 础 知 识 巩 固 高 频 考 向 探 究 解:设扩充后广场的长为3x m,宽为2x m, 依题意得3x·2x·100+30(3x·2x-50×40)=642000, 解得x1=30,x2=-30(舍去). 所以3x=90,2x=60. 答:扩充后广场的长为90 m,宽为60 m. 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 1.[2019·长沙]近日,长沙市教育局出台《长沙市中小学教师志愿辅导工作实施意 见》,鼓励教师参与志愿辅导,某区率先示范,推出名师公益大课堂,为学生提供线 上线下免费辅导.据统计,第一批公益课受益学生2万人次,第三批公益课受益学 生2.42万人次. (1)如果第二批,第三批公益课受益学生人次的增长率相同,求这个增长率; (2)按照这个增长率,预计第四批公益课受益学生将达到多少万人次? 基 础 知 识 巩 固 高 频 考 向 探 究 解:(1)设增长率为x, 根据题意,得:2(1+x)2=2.42, 解得x1=-2.1(舍去),x2=0.1=10%. 答:增长率为10%. 基 础 知 识 巩 固 高 频 考 向 探 究 1.[2019·长沙]近日,长沙市教育局出台《长沙市中小学教师志愿辅导工作实施 意见》,鼓励教师参与志愿辅导,某区率先示范,推出名师公益大课堂,为学生提 供线上线下免费辅导.据统计,第一批公益课受益学生2万人次,第三批公益课受 益学生2.42万人次. (2)按照这个增长率,预计第四批公益课受益学生将达到多少万人次? (2)2.42×(1+0.1)=2.662(万人次). 答:第四批公益课受益学生将达到2.662万人次. 基 础 知 识 巩 固 高 频 考 向 探 究 26 2.[2018·盐城]一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩 大销售,增加盈利,该店采取了降价措施.在每件盈利不少于25元的前提下,经过一 段时间销售,发现销售单价每降低1元,平均每天可多售出2件. (1)若降价3元,则平均每天销售数量为 件; (2)当每件商品降价多少元时,该商店每天销售利润为1200元? (2)设当每件商品降价x元时,该商店每天销售利润为1200元. 由题意,得(40-x)(20+2x)=1200. 整理,得x2-30x+200=0.解得x1=10,x2=20. 又每件盈利不少于25元,∴x=20不合题意,舍去. 答:当每件商品降价10元时,该商店每天销售利润为1200元.查看更多