中考数学专题复习练习：函数的图像经典例题

中考数学专题复习练习：函数的图像经典例题

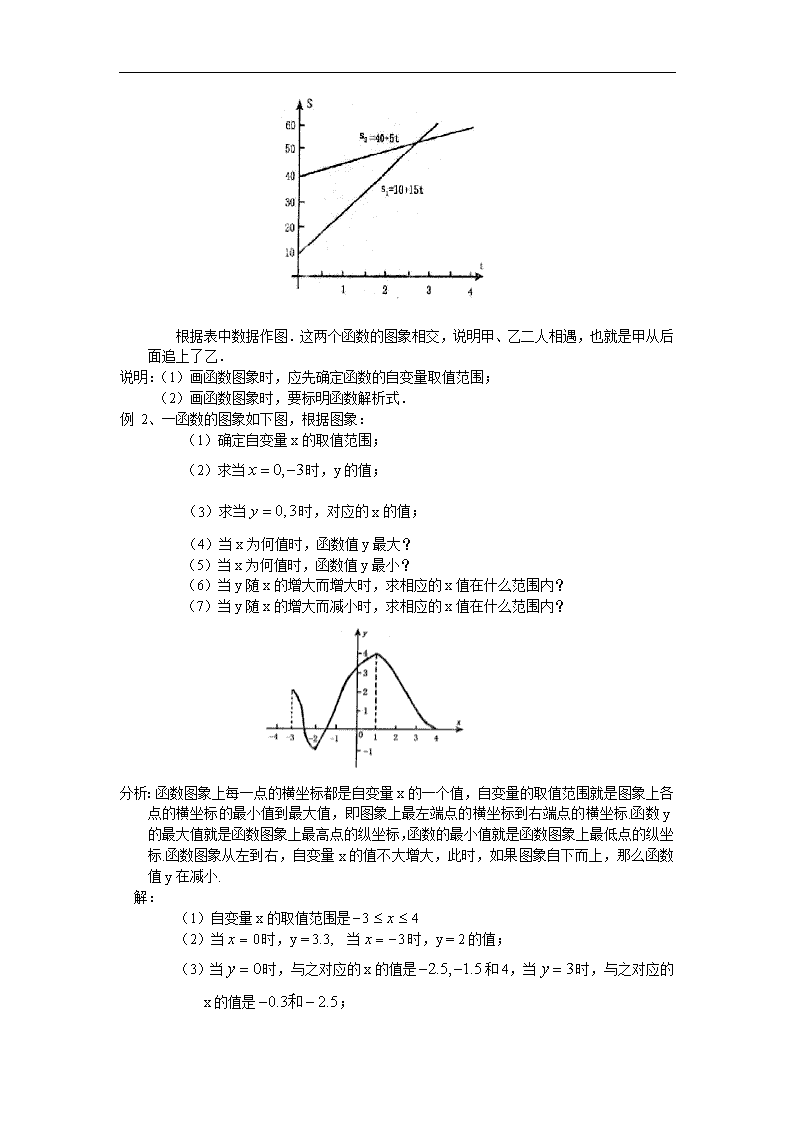
例1 、在赵庄通向省城的公路上，甲乙二人同时向距赵庄60千米的省城进发.甲从距赵庄10千米处以15千米/小时的速度骑自行车，乙从甲前方30千米处以5千米/小时的速度步行.‎ （1） 分别求甲、乙二人与赵庄距离（千米）、（千米）和所用时间（小时）的函数关系式；‎ （2） 在同一坐标系下画出这两个函数的图象.这两个函数图象如果相交说明了什么？‎ 分析：甲距赵庄的距离=10+甲走的距离 ‎　　 即 ；‎ ‎ 同理 ‎ 解：（1）‎ ‎ ‎ ‎ （2）甲走完全程用时为；‎ ‎ 乙走完全程用时为．‎ ‎　　　　又时间 ‎　　　　所以的自变量的取值范围是 ‎　　　　的自变量的取值范围是 列表如下：‎ ‎０‎ ‎１‎ ‎２‎ ‎３‎ ‎10‎ ‎25‎ ‎40‎ ‎55‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎40‎ ‎45‎ ‎50‎ ‎55‎ ‎60‎ 根据表中数据作图．这两个函数的图象相交，说明甲、乙二人相遇，也就是甲从后面追上了乙．‎ 说明：（1）画函数图象时，应先确定函数的自变量取值范围；‎ ‎ （2）画函数图象时，要标明函数解析式．‎ 例 2、一函数的图象如下图，根据图象：‎ ‎ （1）确定自变量x的取值范围；‎ ‎ （2）求当时，y的值；‎ ‎（3）求当时，对应的x的值；‎ ‎（4）当x为何值时，函数值y最大？‎ ‎ （5）当x为何值时，函数值y最小？‎ ‎ （6）当y随x的增大而增大时，求相应的x值在什么范围内？‎ ‎ （7）当y随x的增大而减小时，求相应的x值在什么范围内？‎ 分析：函数图象上每一点的横坐标都是自变量x的一个值，自变量的取值范围就是图象上各点的横坐标的最小值到最大值，即图象上最左端点的横坐标到右端点的横坐标.函数y的最大值就是函数图象上最高点的纵坐标，函数的最小值就是函数图象上最低点的纵坐标.函数图象从左到右，自变量x的值不大增大，此时，如果图象自下而上，那么函数值y在减小.‎ 解： ‎ ‎（1）自变量x的取值范围是 ‎ （2）当时，y = 3.3, 当时，y = 2的值；‎ ‎（3）当时，与之对应的x的值是和4，当时，与之对应的x的值是；‎ ‎（4）当时，y的值最大，此时；‎ ‎ （5）当时，y的值最小，此时，；‎ ‎ （6）当y随x的增大而增大时，相应的x值在＜内；‎ ‎ （7）当y随x的增大而减小时，求相应的x值在内？‎ 说明：（1）用图象法表示函数形象、直观，但不精细，因此，从图象上观察的数值往往是近似值，只有通过具体函数解析式的计算，才能得到精确值.‎ ‎（2）当函数图象从左下到右上呈“撇”状时，函数y随x的增大而增大；当函数图象从左上到右下呈“捺”状时，函数y随x的增大而减小.反之也对.‎ ‎（3）从函数图象求函数的某些值、研究函数y随自变量x的变化规律是数形结合思想的具体体现.‎ 例 3、若点在函数的图象上，且当时，．‎ （1） 求a、c的值；‎ （2） 如果点（-1，m）和点（n ，6）也在函数的图象上，求m ，n的值.‎ 解：（1）点在函数的图象上，‎ ‎ ‎ ‎ 又当时，，‎ ‎ ‎ ‎ 即 ‎ 解 得 ‎ ‎（2）‎ ‎ 函数为 ‎ 点和点在函数图象上 说明：应向学生强调：若点在图象上，则点的横坐标，纵坐标满足这个函数的解析式.‎ ‎　‎ 典型例题四 例 （常州市，2000）小明的父亲饭后出去散步，从家中走20分钟到一个离家900米的报亭看10分钟报纸后，用15分钟返回家里.图中表示小明的父亲离家的时间与距离之间的关系是（ ）.‎ 解 选D.‎ 说明：本题考查函数图象的应用，解题关键是正确理解函数图象与实际问题间的内在联系，易错点是误选C.‎ 典型例题五 例 已知函数与的图象的一个交点是，求其余交点的坐标．‎ 分析：函数图象的交点坐标满足两个函数的解析式，因此，可转化为方程组求解．‎ 解：点是函数与的图象交点，‎ ‎　　‎ ‎　两个函数的解析式分别为与．‎ ‎　　　　　设图象的交点为 则 ‎　　　　　二式相减，得 ‎　　　　　‎ ‎　　　　　分别将代入 ‎　　　　　得　‎ ‎　　　 另外两个交点是（0，0）和（-3，-18）‎ 说明：求函数图象交点问题，通常是转化为方程组求解.‎ 典型例题六 例 （吉林省试题，2002）一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售.售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示，结合图象回答下列题：‎ ‎（1）农民自带的零钱是多少？‎ ‎（2）降价前他每千克土豆出售的价格是多少？‎ ‎（3）降价后他按每千克0.4元将剩余土豆出售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆.‎ 解：（1）农民自带的零钱是5元.‎ ‎ （2）（20－5）÷30＝0.5（元）‎ ‎ 降价前他每千克土豆卖0．5元.‎ ‎ （3）（26－20）÷0.4＋30＝45（千克）‎ ‎ 他一共带了45千克土豆.‎ 说明：本题考查学生的识图能力。能由所给出的函数图象回答问题。‎ 典型例题七 例 如图，是某个篮球运动员在五场比赛中的得分情况，依据图回答：‎ ‎ （1）该运动员第一场球得多少分；‎ ‎ （2）哪场球得分比前一场得分少？‎ ‎ （3）在五场比赛中最高得分是多少？最低得分是多少？‎ ‎ （4）从这五场比赛中的得分情况分析，该运动员的竞技状态怎么样？‎ ‎ 解：（1）这个运动员在第一场比赛中得21分.‎ ‎ （在场次栏中找到“1”，然后在得分栏中找到相应的得分）‎ ‎ （2）第二场球比第一场球得分少，竞技状态趋下.（图形向下）‎ ‎ （3）第五场比赛得分最高为36分，第一场比赛得分最低21分.‎ ‎ （4）从这五场的比赛得分情况看，该运动员目前的竞技状态是向前发展，其趋势是良好的.（从第二场球之后图形全部向上.）‎ 说明：本题考查学生的识图能力。能由所给出的函数图象回答所问的问题。‎ 典型例题八 例 已知点在函数的图象上，且当时，‎ ‎（1）求，的值；（2）如果点和点也在函数的图象上，求，的值.‎ 解：①点和点在函数的图象上 由方程组解出：，‎ 即 ‎（2）依题意，有 ‎（函数问题转化方程组问题）‎ 即，或，‎ 说明：本题利用方程组来解决函数问题．‎ 典型例题九 例 已知函数，求：‎ ‎（1）函数图象与轴、轴的交点坐标；‎ ‎（2）当取什么值时，函数值是正数、零、负数？‎ 解（1）函数图象与轴交点既在图象上，又在轴上 此交点的纵坐标为0，即 ‎（记住坐标轴上点的坐标的特征）‎ ‎，得 ‎（这是求与坐标轴相交点的方法）‎ 函数图象与轴交点坐标是 又函数图象与轴的交点在轴上：‎ 此交点的横坐标为0，即 ‎（这是求与坐标轴相交点的方法）‎ ‎ 得 函数图象与轴的交点是 ‎（2）由函数值大于0，即，从而，得；‎ ‎（转化不等式求解）‎ 选择题 ‎1. 如图分别给出了变量与之间的对应关系，不符合函数定义的是（）.‎ ‎2. 点，，，中，在函数的图象上的点有（）.‎ A．1个 B．2个 C．3个 D．4个 ‎3. 函数的图象过四个点，，，中的（）‎ A．1个 B．2个 C．3个 D．4个 ‎4.下列各点不在函数的图象上的是（）‎ A． B． C． D．‎ ‎5. 直线与的交点在（）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎6.下列各点在的图象上的是（）‎ A． B． C． D．‎ ‎7. 函数与的图象交于点，则点的坐标是（）‎ A． B． C． D．‎ 答案：‎ ‎1. D 2. B 3. B 4. D 5. B 6. C 7. D.‎ 由函数值等于0，即，从而，得；‎ ‎（转化方程求解）‎ 由函数值小于0，即，从而，得 综上，当时，；当时，；当时，.‎ 说明：本题考查函数图象与坐标轴的交点问题,此类问题通常是转化为方程来解。‎ 填空题 ‎1.长方形面积为，则它的宽与之间的函数关系式是________，自变量的取值范围是__________. 2. 函数的自变量的取值范围是________.‎ ‎3. 函数的自变量的取值范围是________.‎ ‎4. 函数，当时，函数的值是_________；当函数时，自变量的值是_________.‎ ‎5. 已知、满足等式，那么.‎ ‎6. 在匀速直线运动中，当路程一定时，用时间来表示速度的函数式是_________.‎ 答案：‎ ‎1. ， 2. 3. 4. ；2 5. 6. .‎ 解答题 ‎1. 画出下列函数图象 ‎（1） （2‎ ‎2. 分别在同一坐标系内画出各组函数的图象，并观察每组图象之间的关系和区别.‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ ‎3．取何值时，下列函数有意义：‎ ‎（1）；（2）；（3）；‎ ‎（4）；（5）‎ ‎4．一根弹簧的长度是，它能挂的重量不能超过，并且每挂重物就伸长，写出挂重物后的弹簧长度与所挂重物之间的函数关系式。‎ ‎5．已知，求当，时，函数的值分别是_________‎ ‎6．求出函数图象上和函数图象上横坐标为和0的坐标。‎ ‎7．已知函数 ‎（1）画出这个函数的图象；‎ ‎（2）写出相应的函数与x轴交点坐标，与y轴的交点坐标；‎ ‎（3）判断点是否在这个函数的图象上，如果在将它画在图象上.‎ 答案：‎ ‎1．略 2. 略 3．（1）的取值范围是全体实数（2）的一切实数 ‎（3）的全体实数（4）且的全体实数 ‎（5）的全体实数 ‎4．‎ ‎5．，‎ ‎6．，，‎ ‎7.（1）略 （2）（2，0），（0，4） （3）P、Q均在图象上.‎ ‎　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　‎ ‎2003年中考类型题 ‎1. ‎ 甲、乙两同学约定游泳比赛规则：甲先游自由泳到泳道中点后改为蛙泳，而乙则是先游蛙泳到泳道中点后改为自由泳，两人同时从泳道起点出发，最后两人同时游到泳道终点。又知甲游自由泳比乙游自由泳速度快，并且二人自由泳均比蛙泳速度快，若某人离开泳道起点的距离s与所用时间t的函数关系可用图象表示，则下列选项中正确的是（ ）‎ ‎ A. 甲是图<1>，乙是图<2> B. 甲是图<3>，乙是图<2>‎ ‎ C. 甲是图<1>，乙是图<4> D. 甲是图<3>，乙是图<4>‎ ‎2．一天，小军和爸爸去登山，已知山脚到山顶的路程为300米，小军先走了一段路程，爸爸才开始出发，图中两条线段分别表示小军和爸爸离开山脚登山的路程s（米）与登山所用的时间t（分钟）的关系（从爸爸开始登山时计时）。根据图象，下列说法错误的是（ ）‎ A．爸爸开始登山时，小军已走了50米 B．爸爸走了5分钟，小军仍在爸爸的前面 C．小军比爸爸晚到山顶 D．爸爸前10分钟登山的速度比小军慢，10分钟之后登山的速度比小军快 ‎ ‎ s(米)‎ ‎ ‎ ‎300‎ ‎50‎ O 10 t(分钟)‎ ‎3．甲乙二人参加某体育项目训练，为了便于研究，把最近五次训练成绩分别用实线和虚线连结，如图所示，下面的错误的是 A．乙的第二次成绩与第五次成绩相同 B．第三次测试甲的成绩与乙的成绩相同 C．第四次测试甲的成绩比乙的成绩多2分 D．五次测试甲的成绩都比乙的成绩高 ‎4．一天，亮亮发烧了，早晨他烧得很厉害，吃过药后感觉好多了，中午时亮亮的体温基本正常，但是下午他的体温又开始上升，直到半夜亮亮才感觉身上不那么发烫了。下面各图能基本上反映出亮亮这一天（0时～24时）体温的变化情况是（　　）‎ ‎5．某游客为爬上3千米高的山顶看日出。先用1小时爬了2千米，休息0.5小时后，再用1小时爬上山顶。游客爬山所用时间t与山高h间的函数关系用图形表示是 小时 小时 小时 小时 ‎　　（Ａ）　　　　　　　　（Ｂ）　　　　　　（Ｃ）　　　　　　　　（Ｄ）‎ ‎6. 一慢车和一快车沿相同路线从A地到B地，所行的路程与时间的函数图象如图所示.试根据图象,回答下列问题:‎ (1) 慢车比快车早出发______小时,快车追上慢车时行驶了______千米,快车比慢车早________小时到达B地；‎ (2) 在下列3个问题中任选一题求解(多做不加分).‎ ‎①快车追上慢车需几个小时?‎ ‎②求慢车、快车的速度.‎ ‎③求A、B两地之间的路程.‎ ‎7．阅读下列材料：“父亲和儿子同时出去晨练。如图，实线表示父亲离家的路程（米）与时间（分钟）的函数图象；虚线表示儿子离家的路程（米）与时间（分钟）的图象。由图象可知，他们在出发10分钟时相遇一次，此时离家400米；晨练了30分钟，他们同时到家。”‎ ‎ 根据阅读材料给你的启示，利用指定的直角坐标系（如图）或用其他方法解答问题：‎ 一巡逻艇和一货轮同时从A港口前往相距100千米的B港口，巡逻艇和货轮的速度分别为100千米/时和20千米/时，巡逻艇不停的往返于A、B两港口巡逻（巡逻艇调头的时间忽略不计）。‎ ‎（1）货轮从A港口出发以后直到B港口与巡逻艇一共相遇了几次？‎ ‎（2）出发多少时间巡逻艇与货轮第三次相遇？此时离A港口多少千米？‎ 参考答案：‎ ‎1．C 2. D 3. D 4. C 5. D 6. （1） 2 ；276；4；（2）① 4小时；② 46千米/小时、69千米/小时；③ 828千米。7. 略