中考数学专题复习练习：中位线

中考数学专题复习练习：中位线

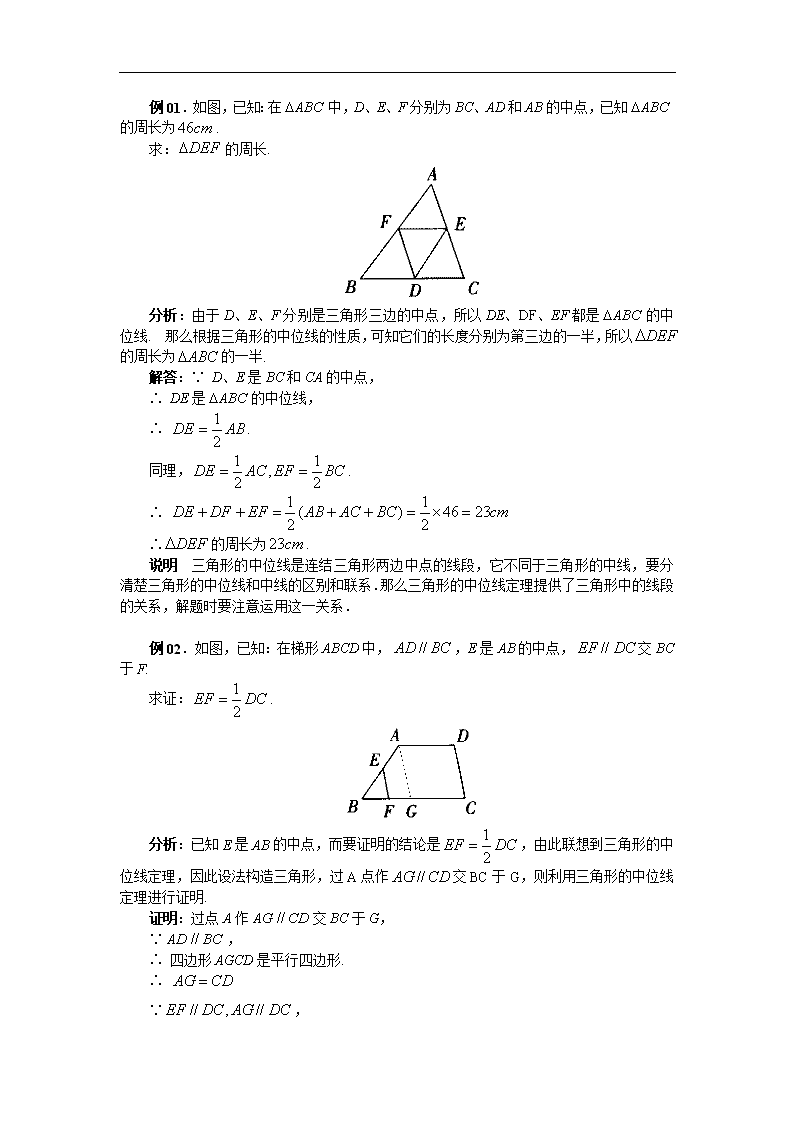
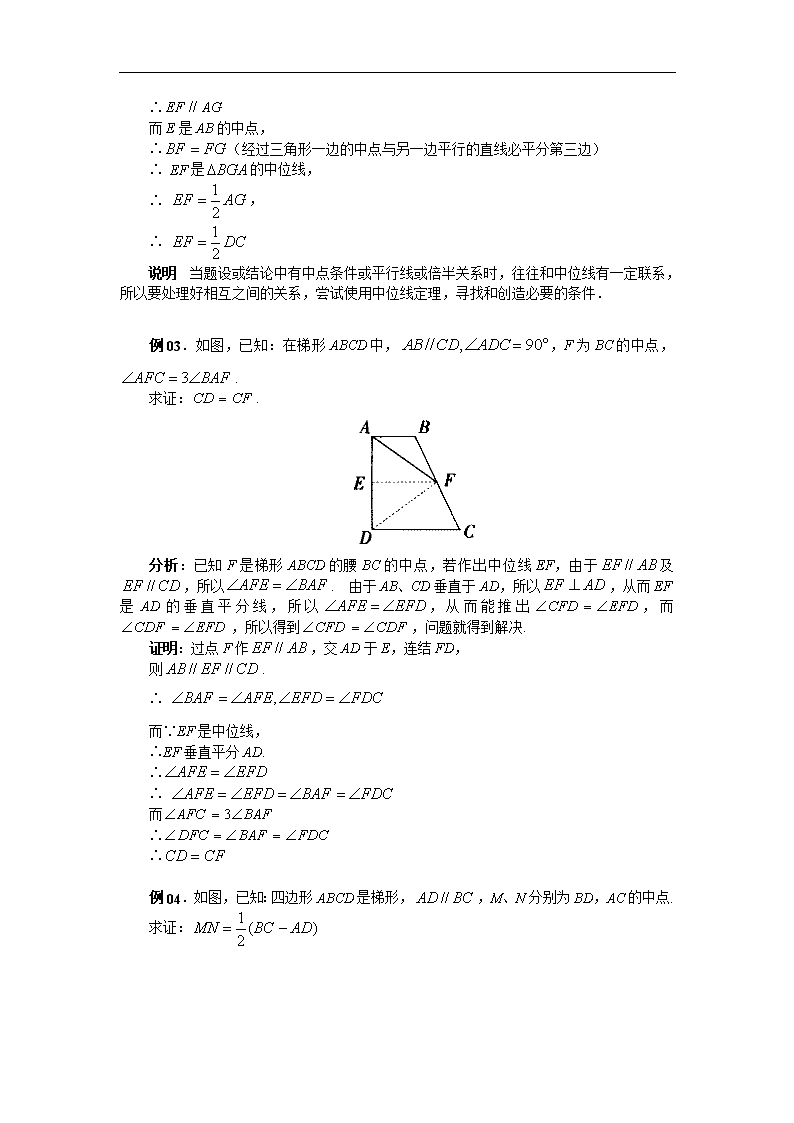
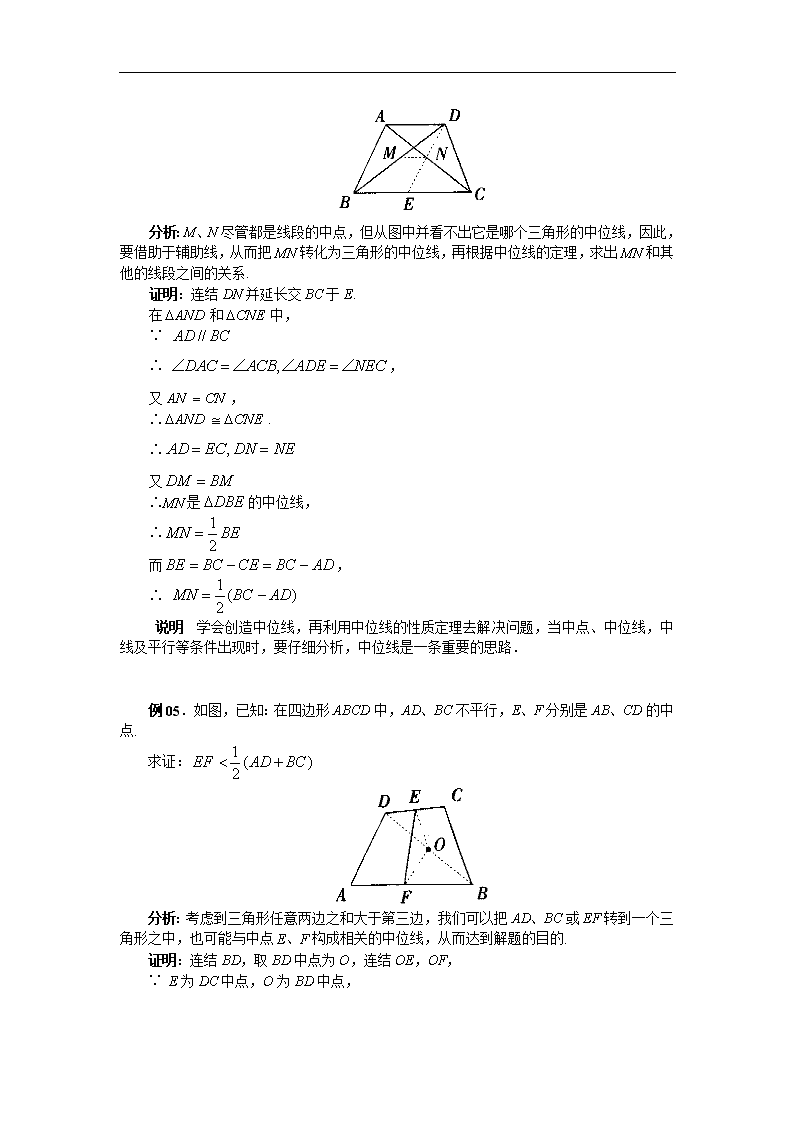
例01．如图，已知：在中，D、E、F分别为BC、AD和AB的中点，已知的周长为. ‎ 求：的周长. ‎ 分析：由于D、E、F分别是三角形三边的中点，所以DE、DF、EF都是的中位线. 那么根据三角形的中位线的性质，可知它们的长度分别为第三边的一半，所以的周长为的一半. ‎ 解答：∵ D、E是BC和CA的中点，‎ ‎∴ DE是的中位线，‎ ‎∴ . ‎ 同理，. ‎ ‎∴ ‎ ‎∴的周长为. ‎ 说明 三角形的中位线是连结三角形两边中点的线段，它不同于三角形的中线，要分清楚三角形的中位线和中线的区别和联系．那么三角形的中位线定理提供了三角形中的线段的关系，解题时要注意运用这一关系．‎ 例02．如图，已知：在梯形ABCD中，，E是AB的中点，交BC于F. ‎ 求证：. ‎ 分析：已知E是AB的中点，而要证明的结论是，由此联想到三角形的中位线定理，因此设法构造三角形，过A点作交BC于G，则利用三角形的中位线定理进行证明. ‎ 证明：过点A作交BC于G，‎ ‎∵， ‎ ‎∴ 四边形AGCD是平行四边形. ‎ ‎∴ ‎ ‎∵， ‎ ‎∴‎ 而E是AB的中点，‎ ‎∴（经过三角形一边的中点与另一边平行的直线必平分第三边）‎ ‎∴ EF是的中位线，‎ ‎∴ ， ‎ ‎∴ ‎ ‎ 说明 当题设或结论中有中点条件或平行线或倍半关系时，往往和中位线有一定联系，所以要处理好相互之间的关系，尝试使用中位线定理，寻找和创造必要的条件．‎ 例03．如图，已知：在梯形ABCD中，，F为BC的中点，. ‎ 求证：. ‎ 分析：已知F是梯形ABCD的腰BC的中点，若作出中位线EF，由于及，所以. 由于AB、CD垂直于AD，所以，从而EF是AD的垂直平分线，所以，从而能推出，而，所以得到，问题就得到解决. ‎ 证明：过点F作，交AD于E，连结FD，‎ 则. ‎ ‎∴ ‎ 而∵EF是中位线，‎ ‎∴EF垂直平分AD. ‎ ‎∴ ‎ ‎∴ ‎ 而 ‎∴ ‎ ‎∴‎ 例04．如图，已知：四边形ABCD是梯形，，M、N分别为BD，AC的中点. ‎ 求证：‎ 分析：M、N尽管都是线段的中点，但从图中并看不出它是哪个三角形的中位线，因此，要借助于辅助线，从而把MN转化为三角形的中位线，再根据中位线的定理，求出MN和其他的线段之间的关系. ‎ 证明：连结DN并延长交BC于E. ‎ 在和中，‎ ‎∵ ‎ ‎∴ ，‎ 又，‎ ‎∴. ‎ ‎∴‎ 又 ‎ ‎∴MN是的中位线，‎ ‎∴ ‎ 而，‎ ‎∴ ‎ ‎ 说明 学会创造中位线，再利用中位线的性质定理去解决问题，当中点、中位线，中线及平行等条件出现时，要仔细分析，中位线是一条重要的思路．‎ 例05．如图，已知：在四边形ABCD中，AD、BC不平行，E、F分别是AB、CD的中点. ‎ 求证：‎ 分析：考虑到三角形任意两边之和大于第三边，我们可以把AD、BC或EF转到一个三角形之中，也可能与中点E、F构成相关的中位线，从而达到解题的目的. ‎ 证明：连结BD，取BD中点为O，连结OE，OF，‎ ‎∵ E为DC中点，O为BD中点，‎ ‎∴ ‎ 同理可证：‎ 而在中，，‎ ‎∴ ‎ 即 说明：构造中位线的方法如能恰当使用，能使证题走上捷径. ‎ 例06．如图，等腰梯形ABCD的周长是，如果它的中位线EF与腰长相等，它们的高是. ‎ 求这个梯形的面积. ‎ 解答：∵，且. ‎ ‎∴，‎ 即 ‎∴. ‎ 说明 本题考查梯形的中位线性质定理及梯形的面积，易错点是忽视用公式，解题关键是求中位线的长. ‎ 例07．如图，在中，，于D，M为BC的中点. ‎ 求证：. ‎ 证明：取AB的中点N，连结DN，MN. ‎ ‎∵，‎ ‎∴. ‎ 又∵M是BC的中点，‎ ‎∴ ‎ ‎∴‎ ‎∴，‎ ‎∴‎ 又∵‎ ‎∴ ‎ ‎∴ ‎ ‎∴. ‎ 说明 本题考查了三角形中位线定理的应用，解题关键是取AB的中点N，连结ND，NM，利用三角形中位线定理及等腰三角形的判定证明. ‎ 例08．已知：在中，，CD是中线，延长AB到E，使，连结CE. ‎ 求证：. ‎ 证法1 如图，取CE的中点F，连结BF，则BF是的中位线. ‎ ‎∴. ‎ 又，‎ ‎∴‎ ‎∵，‎ ‎∴‎ ‎∵，‎ ‎∴‎ ‎∴‎ 又，‎ ‎∴‎ ‎∴ ‎ ‎∵，‎ ‎∴‎ 证法2 如图，取AC中点F，连结BF，则BF是的中位线. ‎ ‎∴ ‎ ‎∵，‎ ‎∴ ‎ ‎∴ ‎ ‎∴‎ 证法3 如图，取BC中点G，BE中点F，连结DG，FG. 则，. ‎ ‎∴. ‎ ‎∴‎ ‎∵‎ ‎∴. ‎ ‎∴ ‎ ‎∴‎ 说明 构造和利用中位线是解题关键 例09．如图，已知梯形ABCD中，，对角线AC，BD相交于O，，，，分别是AO，BO，CO，DO的中点. ‎ 求证：四边形是梯形. ‎ 错证：∵，，，分别是AO，BO，CO，DO的中点, ‎ ‎∴,分别是，的中位线. ‎ ‎∴.又，‎ ‎∴‎ ‎∴四边形是梯形. ‎ 正解：∵，，，分别是AO，BO，CO，DO的中点，‎ ‎∴,分别是，的中位线. ‎ ‎∴. ‎ ‎∴‎ 同理 ，‎ 又∵四边形ABCD是梯形，‎ ‎∴AB与DC不平行. ‎ ‎∴与也不平行. ‎ ‎∴四边形是梯形. ‎ 说明 错证中没有证明与不平行. ‎ 例10．如图，ABCD为等腰梯形，，对角线AC，BD交于O，且. 又E，F，G分别为DO，AO，BC的中点. ‎ 求证：为等边三角形. ‎ 证明：连EC. ∵‎ ‎∴，且 ‎∵ ‎ ‎∴，‎ ‎∴为等腰三角形. ‎ ‎∵，‎ ‎∴为等边三角形. ‎ 又∵E为OD中点，‎ ‎∴‎ 在中，G为斜边的中点，‎ ‎∴‎ 同理连BF. 可证 在中，‎ ‎∵E，F分别为OD，OA的中点，‎ ‎∴. ‎ ‎∴为等边三角形. ‎ 说明 辅助线的添加是关键 例11．如图，C为已知线段AB外一点，以AC，BC为边，分别向的外侧作正方形ACFD和正方形BCGE，不论C点的位置在AB的同侧怎样变化，‎ 求证：（1）D，E到AB所在直线的距离之和为定值；‎ ‎（2）线段DE的中点M为定点. ‎ 证明：（1）作于，于，于. ‎ ‎∵，且 ‎∴‎ ‎∴ ‎ ‎∴‎ ‎∴ ‎ ‎∴‎ ‎∴ ‎ ‎∴. ‎ 同理：‎ ‎∴（为定值）‎ ‎（2）过M作于N. ‎ ‎∵ ，‎ ‎∴‎ ‎∵，‎ ‎∴ ‎ ‎∵ ，‎ ‎∴‎ ‎∴ ‎ ‎∴‎ ‎∴ ‎ ‎∴. ‎ 即N为AB的中点（为定点）‎ 又∵（为定值），‎ ‎∴M为定点. ‎ 分析 本题综合考查了平行线等分线段定理，梯形中位线定理及全等三角形的判定与性质等，易错点是对定值、定点不理解，解题关键是作如图所示的四条辅助线. ‎ 选择题 ‎1．顺次连结平行四边形各边中点所得的四边形一定是（ ）‎ A．菱形 B．矩形 C．梯形 D．平行四边形 ‎2．一个梯形的中位线长为，两对角线互相垂直，则这梯形的高为（ ）‎ A． B． C． D．不能确定其大小 ‎3．已知三角形的三条中位线分别为，则这个三角形的周长是（ ）‎ A． B． C． D．‎ ‎4．若等腰梯形两底角为，腰长为，高和上底相等，那么梯形中位线长为（ ）‎ A． B． C． D．‎ ‎5．（北京市昌平区，2001）如果梯形一底长为6，中位线长为8，那么另一底长为（ ）‎ A．14 B．10 C．8 D．4‎ ‎6．（南通市，2001）如果，梯形ABCD中，，EF是中位线，，，则BC的长是（ ）‎ A． B． C． D．‎ ‎7．（威海市，2001）下面有三种说法：‎ ‎①任意四边形两组对边中点的连线互相平分 ‎②任意三角形的一条中位线与第三边上的中线互相平分 ‎③梯形的两条对角线可能互相平分 正确的是 A．①②③ B．①② C．①③ D．②③‎ 参考答案：‎ ‎1．D 2．A 3．B 4．C 5．B 6．C 7．B ‎ 选择题 ‎1．顺次连结等腰梯形四边中点所组成的四边形是（ ）‎ ‎ A．矩形 B．梯形 C．菱形 D．正方形 ‎2．（北京市东城区，2001）如图，DE是的中位线，F是DE的中点，BF的延长线交AC于点H，则等于（ ）‎ A． B． C． D．‎ ‎3．（荆州市，2002）如图，在梯形ABCD中，，，且，则的面积与的面积比为（ ）‎ A． B． C． D．‎ ‎4．（呼和浩特市，2002）梯形的中位线长为，一条对角线把中位线分成两部分，则梯形的两底分别为（ ）‎ A．和 B．和 C．和 D．和 ‎5．（陕西省，2002）如图，在中，D，E，F分别是边AB，BC，AC的中点，若的周长为，则的周长为（ ）‎ A． B． C． D．‎ ‎6．（北京市西城区，2002）斜拉桥是利用一组组钢索，把桥面重力传递到耸立在两侧的高塔上的桥梁，它不须建造桥墩. 如图中，，，…，是斜拉桥上5条互相平行的钢索，并且，，，，，被均匀地固定在桥上. 如果最长的钢索，最短的钢索，那么钢索，的长分别为（ ）‎ A．、 B．、 C．、 D．、‎ 参考答案：‎ ‎1．解：如图，连结AC，BD. ‎ ‎∵ABCD是等腰梯形，∴.‎ ‎∵EF，HG，EH，FG是三角形中位线，‎ ‎∴. ‎ ‎∴ . ‎ ‎∴四边形EFGH是平行四边形. ‎ 又，. ∴‎ ‎∴EFGH是菱形，故应选C. ‎ ‎2．B 3．C 4．D 5．C 6．A ‎ 填空题 ‎1．（山东省菏泽地区，2001）直角梯形的一条对角线将它分成两个三角形，其中一个是等边三角形，如果它的中位线长为，那么它的下底长是______. ‎ ‎2．（泉州市，2001）已知梯形上、下底长分别为3和5，则中位线长为_____. ‎ ‎3．（北京市石景山区，2001）如果梯形的上底长与下底长的比为，中位线的长为24，那么梯形的下底长为_____. ‎ ‎4．（江西省，2001）如图，等腰梯形ABCD中，，，于点E，，则这个梯形的中位线长为_______. ‎ ‎5．（龙岩市、宁德市，2001）如图，EF是的中位线，BD平分交EF于D，若，则______. ‎ ‎6．（北京市石景山区，2002）如图，在梯形ABCD中，，中位线EF交对角线BD于点O，，且，则_______. ‎ ‎7．（青海省，2002）等腰梯形中，已知一个底角是，高为，中位线长为，则梯形的上底长是______. ‎ ‎8．（绍兴市，2002）如图，梯形ABCD中，，，，，点E在DC上，AE、BC的延长线相交于点F. 若，则的值是______. ‎ ‎9．（天津市，2002）如图，梯形ABCD中，，对角线，且，，则该梯形的中位线的长等于______. ‎ ‎10．（徐州市，2002）如图，在梯形ABCD中，，则该梯形的中位线长为______，若，且，则EF的长为_____. ‎ ‎11．（安徽省，2002）如图，在中，，，，，是AB 边的五等分点，，，，是AC边的五等分点，则_____. ‎ ‎12．（江西省，2002）如图，要测量A，B两点间距离，在O点设桩，取OA中点C，OB中点D，测得米，则_______米. ‎ ‎13．（湖州市，2001）如图，已知直角梯形ABCD的中位线EF的长为，垂直于底的腰AB的长为，则的面积等于______. ‎ ‎14．‎ 参考答案：‎ ‎1． 2．4 3．32 4．4 5．2 6．16 ‎ ‎7． 8．30，48 9． 10．2， 11． 12． ‎ ‎13．‎ 解答题 ‎1．如图，等腰梯形ABCD中，，中位线EF交AC于G，且AC平分，，. ‎ 求梯形ABCD的周长. ‎ ‎2．如图，在梯形ABCD中，，E，F分别是对角线AC，BD的中点. ‎ 求证：四边形ADEF是平行四边形. ‎ ‎3．（哈尔滨市，2002）如图，已知MN是梯形ABCD的中位线，AC，BD与MN交于F，E，，求EF的长. ‎ ‎4．已知：如图，中，C是DB上一点，，，且. ‎ 求证：‎ ‎5．已知：如图，中，AD为中线，过B的直线交AD于F，交AC于E，且. ‎ 求证：. ‎ ‎6．已知：如图，中，E是BC的中点，D是CA的延长线上的一点，，DE交AB于F. ‎ 求证：. ‎ ‎7．（泰州市，2001）求证：三角形的一条中位线与第三边上的中线互相平分（如图）‎ ‎8．如图，梯形ABCD中，，的平分线CE交AB的中点E. ‎ 求证：. ‎ ‎9． 如图，四边形ABCD中，对角线AC，BD交于O，已知，M，N分别是AD，BC中点，MN与AC，BD分别相交于E，F. ‎ 求证：. ‎ ‎10．如图，和形外直线，中线AD延长线交于，，，，，，为垂足. ，‎ 求证：. ‎ ‎11．如图，中，BM，CN平分，的外角，于M，于N. ‎ 求证：. ‎ ‎12．（黄冈市，2002）如图，在梯形ABCD中，，且BD 平分，若梯形的周长为，求此梯形的中位线长. ‎ ‎13．（济南市，2001）如图，中，. 若，分别是AB，AC的中点，则；‎ 若，分别是、的中点，则；‎ 若，分别是、的中点，则；‎ ‎……‎ 若，分别是、的中点，则_____（，且为整数）‎ ‎14．（绍兴市，2002）如图，某斜拉桥的一组钢索共五条，它们相互平行，钢索与桥面的固定点，，，，中，每相邻两点等距离. ‎ ‎（1）问至少需知道几条钢索的长，才能计算出其余钢索的长？‎ ‎（2）请你对（1）中需知道的几条钢索长给出具体数值，并由此计算出其余钢索的长. ‎ 参考答案：‎ ‎1． ‎ ‎2．先证，则，又，故结论成立. ‎ ‎3．解：∵MN是梯形ABCD的中位线，‎ ‎∴. ‎ ‎∵，则. 同理. ‎ 在中，；在中，. ‎ ‎∴ ‎ ‎ ‎ ‎4．解法1：延长AC至G，使，连结DG；‎ 解法2：取AD的中点E，连结CE ‎5．解法1：取BE中点M，连结DM，‎ 解法2：取EC中点M，连结DM ‎6．证法1：如图，取AC的中点G，连结EG. ‎ ‎∵，∴‎ 又E，G分别是BC，AC的中点，∴，即. ∴. ‎ 证法2：如图，过点E作与AB交于H. ‎ ‎∵E是BC中点， ∴H是AB的中点. ∴‎ 又∵，∴. ‎ ‎∵， ，，‎ ‎∴，∴‎ ‎7．证 ‎8．连DE，取CD中点F，连EF，先证是，‎ 则，而，∴ ‎ ‎9．取AB中点G，连MG，NC ‎10．作于 ‎11．延长AM，AN分别交CB，BC的延长线于E，F，证MN是的中位线 ‎12．‎ ‎13． ‎ ‎14．（1）2条；（2）取，则