2020-2021学年陕西省西安市灞桥区铁一中滨河学校八年级上学期期中数学试卷 （解析版）

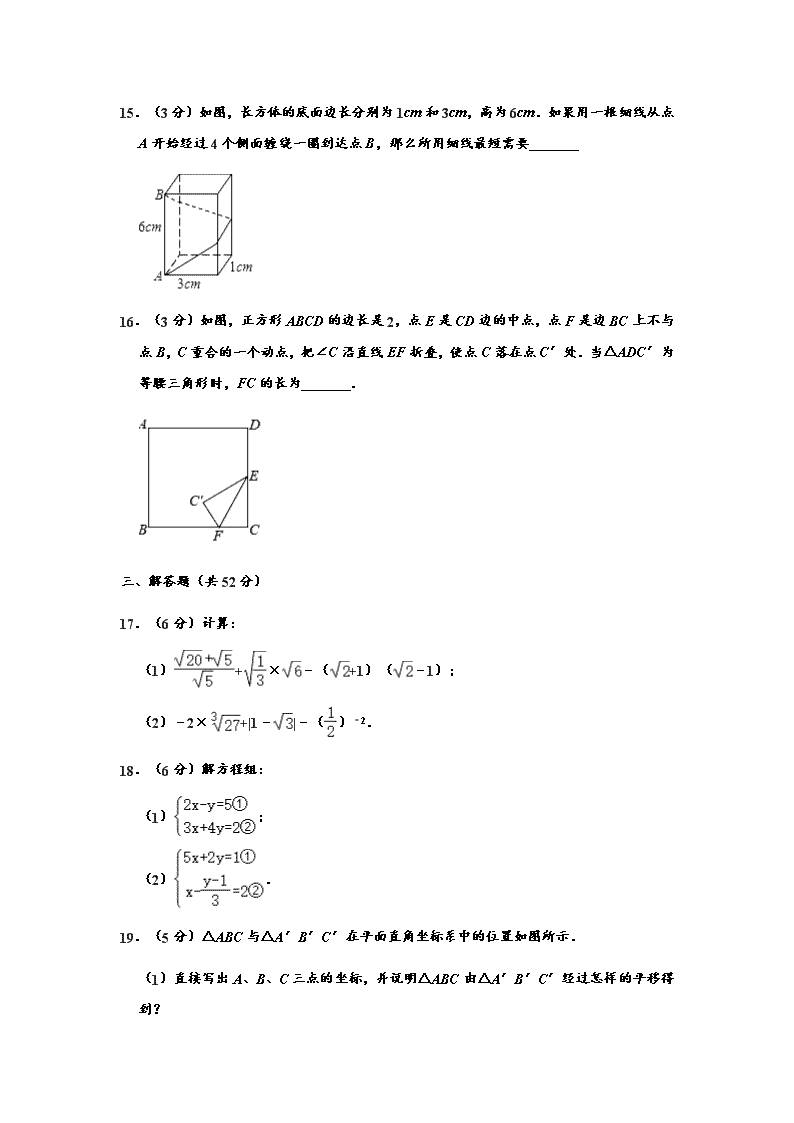
2020-2021学年陕西省西安市灞桥区铁一中滨河学校八年级上学期期中数学试卷 （解析版）

2020-2021 学年陕西省西安市灞桥区铁一中滨河学校八年级第一 学期期中数学试卷 一、选择题 1．（3 分） 的算术平方根是（ ） A．±2 B．2 C．±4 D．4 2．（3 分）在下列各数中： ，3.1415926， ，﹣ ， ， ，0.5757757775…（相 邻两个 5 之间的 7 的个数逐次加 1），无理数有（ ）个． A．1 B．2 C．3 D．4 3．（3 分）在下列各式中正确的是（ ） A． B． C． D． 4．（3 分）已知△ABC 中，a、b、c 分别是∠A、∠B、∠C 的对边，下列条件中不能判断 △ABC 是直角三角形的是（ ） A．∠A：∠B：∠C＝3：4：5 B．∠C＝∠A﹣∠B C．a2﹣b2＝c2 D．a：b：c＝6：8：10 5．（3 分）已知点 P 的坐标为（﹣5，m2+1），则点 P 一定在（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 6．（3 分）若一个正比例函数的图象经过 A（1，﹣2），B（a﹣1，4）两点，则 a 的值为 （ ） A．﹣1 B．0 C．1 D．2 7．（3 分）若式子 +（k﹣1）0 有意义，则一次函数 y＝（1﹣k）x+k﹣1 的图象可能是 （ ） A． B． C． D． 8．（3 分）若点（a，y1）、（a+1，y2）在直线 y＝kx+2 上，且 y1＞y2，则该直线所经过的 象限是（ ） A．第一、二、三象限 B．第一、二、四象限 C．第二、三、四象限 D．第一、三、四象限 9．（3 分）已知梯形 ABCD 的四个顶点的坐标分别是 A（﹣1，0）、B（4，0）、C（3，5）、 D（0，5），直线 y＝﹣3x+b 将梯形分成面积相等的两部分，则 b 的值为（ ） A．5 B． C．7 D． 10．（3 分）在平面直角坐标系中，已知点 A（1，3）和点 B（3，1），点 C、D 分别是 x 轴，y 轴上的动点，则四边形 ABCD 的周长最小值为（ ） A．5 B．6 C．2 +2 D．8 二、填空题（每题 3 分，共 18 分） 11．（3 分）比较大小： （填“＞”“＜”“＝”）． 12．（3 分）将直线 y＝ax+5 的图象向下平移 2 个单位后，经过点 A（2，1），则平移后的 直线解析式为 ． 13．（3 分）若 2xa+2b﹣3﹣ya+b＝3 是关于 x、y 的二元一次方程，则（a+b）2020＝ ． 14．（3 分）已知直线 y＝2x+1 与 y＝﹣x+b 的交点为（﹣1，a），则方程组 的解 为 ． 15．（3 分）如图，长方体的底面边长分别为 1cm 和 3cm，高为 6cm．如果用一根细线从点 A 开始经过 4 个侧面缠绕一圈到达点 B，那么所用细线最短需要 16．（3 分）如图，正方形 ABCD 的边长是 2，点 E 是 CD 边的中点，点 F 是边 BC 上不与 点 B，C 重合的一个动点，把∠C 沿直线 EF 折叠，使点 C 落在点 C′处．当△ADC′ 为等腰三角形时，FC 的长为 ． 三、解答题（共 52 分） 17．（6 分）计算： （1） + × ﹣（ +1）（ ﹣1）； （2）﹣2× +|1﹣ |﹣（ ）﹣2． 18．（6 分）解方程组： （1） ； （2） ． 19．（5 分）△ABC 与△A′B′C′在平面直角坐标系中的位置如图所示． （1）直接写出 A、B、C 三点的坐标，并说明△ABC 由△A′B′C′经过怎样的平移得 到？ （2）求△ABC 的面积． 20．（6 分）如图，在四边形 ABCD 中，AB＝AD，∠BAD＝∠ACD＝90°，BE⊥AC 于 E． （1）求证：BE＝AC； （2）若 AB＝10，CD＝6，求四边形 ABCD 的面积． 21．（6 分）习近平在决战决胜脱贫攻坚座谈会上强调：坚决克服新冠肺炎疫情影响，坚决 夺取脱贫攻坚战全面胜利.2020 年是脱贫攻坚战最后一年，收官之年又遭遇疫情影响，各 项工作任务更重，要求更高．某地的苹果产业成为该地农民打赢脱贫攻坚战的利器，已 知该地有甲、乙两个苹果园，盛产的苹果品质相同，现两个苹果园推出了不同的销售方 案，甲苹果园：不论一次购买数量是多少，价格均为 6 元/kg；乙苹果园：一次购买数量 不超过 50kg 时，价格均为 7 元/kg，超过 50kg，则超出部分的价格按 5 元/kg 计．设某水 果店在同一个苹果园一次购买苹果的数量为 xkg（x＞0）． （1）设在甲苹果园花费 y1 元，在乙苹果园花费 y2 元，分别求 y1，y2 关于 x 的函数关系 式； （2）若该水果店计划用 360 元来购进苹果，则它在甲、乙哪个苹果园中购买苹果的数量 较多？ 22．（6 分）如图，在平面直角坐标系中，一次函数 y＝kx+b 的图象经过点 A（﹣2，6）， 且与 x 轴相交于点 B，与正比例函数 y＝3x 的图象相交于点 C．点 C 的横坐标为 1． （1）求 k、b 的值； （2）若点 D 是直线 AB 上一点，且满足 S△COD＝ S△BOC，求点 D 的坐标． 23．（7 分）已知 A、B 两地之间有一条长 240 千米的公路．甲车从 A 地出发匀速开往 B 地，甲车出发两小时后，乙车从 B 地出发匀速开往 A 地，两车同时到达各自的目的地．两 车行驶的路程之和 y（千米）与甲车行驶的时间 x（时）之间的函数关系如图所示． （1）甲车的速度为 千米/时，a 的值为 ． （2）求乙车出发后，y 与 x 之间的函数关系式． （3）当甲、乙两车相距 100 千米时，求甲车行驶的时间． 24．（10 分）（1）如图 1，已知直线 y＝﹣ x+4 与 y 轴交于 A 点，与 x 轴交于 B 点，将 线段 AB 绕点 B 顺时针旋转 90 度，得到线段 CB，求点 C 的坐标； （2）如图 2，正方形 ABCO，O 为坐标原点，B 的坐标为（﹣5，5），A，C 分别在坐 标轴上，P 是线段 BC 上动点，已知点 D 在第二象限，且是直线 y＝﹣2x﹣1 上的一点， 点 Q 是平面内任意一点，若四边形 ADPQ 是正方形，请直接写出所有符合条件的点 D 的坐标． （3）如图 3，西安铁一中滨河学校为了庆祝 2021 年元且联欢，在一块由三条小路（分 别是 x 轴和直线 AB：y＝﹣ x+4、直线 AC：y＝﹣2x﹣1）围成的三角形区域内计划搭 建一个三角形的特色场地．如图，D（4，0），△DEF 的顶点 E、F 分别在线段 AB、AC 上，且∠DEF＝90°，DE＝EF，试求出该特色场地（△DEF）的面积． 参考答案 一、选择题（每题 3 分，共 30 分） 1．（3 分） 的算术平方根是（ ） A．±2 B．2 C．±4 D．4 解：∵ ＝4， ∴而 4 的算术平方根是 2， ∴ 的算术平方根是 2． 故选：B． 2．（3 分）在下列各数中： ，3.1415926， ，﹣ ， ， ，0.5757757775…（相 邻两个 5 之间的 7 的个数逐次加 1），无理数有（ ）个． A．1 B．2 C．3 D．4 解： ，﹣ ， ，0.5757757775…（相邻两个 5 之间的 7 的个数逐次加 1）是无理 数， 故选：D． 3．（3 分）在下列各式中正确的是（ ） A． B． C． D． 解：∵ ＝3， ∴选项 A 不符合题意； ∵± ＝±2， ∴选项 B 不符合题意； ∵ ＝4， ∴选项 C 不符合题意； ∵ ＝3， ∴选项 D 符合题意． 故选：D． 4．（3 分）已知△ABC 中，a、b、c 分别是∠A、∠B、∠C 的对边，下列条件中不能判断 △ABC 是直角三角形的是（ ） A．∠A：∠B：∠C＝3：4：5 B．∠C＝∠A﹣∠B C．a2﹣b2＝c2 D．a：b：c＝6：8：10 解：A、∠A：∠B：∠C＝3：4：5，且∠A+∠B+∠C＝180°，所以∠C＝75°≠90°， 故△ABC 不是直角三角形； B、因为∠C＝∠A﹣∠B，且∠A+∠B+∠C＝180°，所以∠A＝90°，故△ABC 是直角 三角形； C、因为 a2﹣b2＝c2，a2＝b2+c2，故△ABC 是直角三角形； D、因为 a：b：c＝6：8：10，62+82＝102，故△ABC 是直角三角形． 故选：A． 5．（3 分）已知点 P 的坐标为（﹣5，m2+1），则点 P 一定在（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 解：∵m2≥0， ∴m2+1＞0， ∴点 P（﹣5，m2+1）一定在第二象限． 故选：B． 6．（3 分）若一个正比例函数的图象经过 A（1，﹣2），B（a﹣1，4）两点，则 a 的值为 （ ） A．﹣1 B．0 C．1 D．2 解：设该正比例函数的解析式为 y＝kx（k≠0），则 ， 解得 ． 故选：A． 7．（3 分）若式子 +（k﹣1）0 有意义，则一次函数 y＝（1﹣k）x+k﹣1 的图象可能是 （ ） A． B． C． D． 解：∵式子 +（k﹣1）0 有意义， ∴ ，解得 k＞1， ∴1﹣k＜0，k﹣1＞0， ∴一次函数 y＝（1﹣k）x+k﹣1 的图象过一、二、四象限． 故选：C． 8．（3 分）若点（a，y1）、（a+1，y2）在直线 y＝kx+2 上，且 y1＞y2，则该直线所经过的 象限是（ ） A．第一、二、三象限 B．第一、二、四象限 C．第二、三、四象限 D．第一、三、四象限 解：∵a＜a+1，且 y1＞y2， ∴y 随 x 的增大而减小， 因此 k＜0， 当 k＜0，b＝2＞0 时，一次函数的图象过一、二、四象限， 故选：B． 9．（3 分）已知梯形 ABCD 的四个顶点的坐标分别是 A（﹣1，0）、B（4，0）、C（3，5）、 D（0，5），直线 y＝﹣3x+b 将梯形分成面积相等的两部分，则 b 的值为（ ） A．5 B． C．7 D． 解：如图，∵梯形 ABCD 的四个顶点的坐标分别是 A（﹣1，0）、B（4，0）、C（3，5）、 D（0，5）， ∴AB＝5，CD＝3， ∵直线 y＝﹣3x+b 与线段 CD、AB 交于点 E、F， ∴E 点的坐标为：（ ，5），F 点的坐标为：（ ，0）， ∴DE＝ ，AF＝1+ ， ∵直线 y＝﹣3x+b 平分梯形 ABCD 的面积， ∴梯形 AFED 的面积＝ 梯形 ABCD 的面积， 即： （DE+AF）•h＝ （DC+AB）•h， ∴（ +1+ ）＝ （3+5）， 整理得：2b＝14， ∴b＝7， 故选：C． 10．（3 分）在平面直角坐标系中，已知点 A（1，3）和点 B（3，1），点 C、D 分别是 x 轴，y 轴上的动点，则四边形 ABCD 的周长最小值为（ ） A．5 B．6 C．2 +2 D．8 解：如图，点 A（1，3）关于 y 轴的对称点 A′的坐标是（﹣1，3）， 点 B（3，1）关于 x 轴的对称点 B′的坐标是（3，﹣1）， 由对称性可知 AB+BC+CD+DA＝AB+B′C+CD+DA′≥AB+A′B′， 由勾股定理可求得 AB＝ ＝2 ，A′B′＝ ＝ 4 ， 所以，四边形 ABCD 周长的最小值是 AB+A'B′＝6 ， 故选：B． 二、填空题（每题 3 分，共 18 分） 11．（3 分）比较大小： ＞ （填“＞”“＜”“＝”）． 解：∵ ﹣1＞1， ∴ ＞ ． 故填空结果为：＞． 12．（3 分）将直线 y＝ax+5 的图象向下平移 2 个单位后，经过点 A（2，1），则平移后的 直线解析式为 y＝﹣x+3 ． 解：直线 y＝ax+5 的图象向下平移 2 个单位后得 y＝ax+3， ∵经过点（2，1）， ∴1＝2a+3， 解得：a＝﹣1， 平移后的直线的解析式为 y＝﹣x+3， 故答案为：y＝﹣x+3． 13．（3 分）若 2xa+2b﹣3﹣ya+b＝3 是关于 x、y 的二元一次方程，则（a+b）2020＝ 1 ． 解：∵2xa+2b﹣3﹣ya+b＝3 是关于 x、y 的二元一次方程， ∴ ， 解得：a＝﹣2，b＝3， ∴（a+b）2020＝（﹣2+3）2020＝1， 故答案为：1． 14．（3 分）已知直线 y＝2x+1 与 y＝﹣x+b 的交点为（﹣1，a），则方程组 的解 为 ． 解：把（﹣1，a）代入 y＝2x+1 得 a＝﹣2+1＝﹣1， 即直线 y＝2x+1 与 y＝﹣x+b 的交点为（﹣1，﹣1），则方程组 的解为 ． 故答案为 ． 15．（3 分）如图，长方体的底面边长分别为 1cm 和 3cm，高为 6cm．如果用一根细线从点 A 开始经过 4 个侧面缠绕一圈到达点 B，那么所用细线最短需要 10cm 解：将长方体展开，如图，连接 A、B′， ∵AA′＝1+3+1+3＝8（cm），A′B′＝6cm， ∴根据两点之间线段最短，AB′＝ ＝10cm． 16．（3 分）如图，正方形 ABCD 的边长是 2，点 E 是 CD 边的中点，点 F 是边 BC 上不与 点 B，C 重合的一个动点，把∠C 沿直线 EF 折叠，使点 C 落在点 C′处．当△ADC′ 为等腰三角形时，FC 的长为 或 1 ． 解：由题意 DE＝EC＝EC′＝1， ∴DC′＜1+1 ∴DC′≠DA，只要分两种情形讨论即可： ① 如图 1 中，当 AD＝AC′＝2 时，连接 AE． ∵AE＝AE，AD＝AC′，DE＝DC′， ∴△ADE≌△AC′E， ∴∠ADE＝∠AC′E＝90°， ∵∠C＝∠FC′E＝90°， ∴∠AC′E+∠FC′E＝180°， ∴A、C′、F 共线，设 CF＝x，则 BF＝2﹣x，AF＝2+x， 在 Rt△ABF 中，22+（2﹣x）2＝（2+x）2， 解得 x＝ ． ② 如图 2 中，当点 F 在 BC 中点时，易证 AC′＝DC′，满足条件，此时 CF＝1． 综上所述，满足条件的 CF 的长为 或 1． 故答案为 或 1． 三、解答题（共 52 分） 17．（6 分）计算： （1） + × ﹣（ +1）（ ﹣1）； （2）﹣2× +|1﹣ |﹣（ ）﹣2． 解：（1）原式＝ ＝ ＝3+ ﹣1 ＝2+ ； （2）原式＝ ＝ ＝ ． 18．（6 分）解方程组： （1） ； （2） ． 解：（1） ① ×4+ ② ，得 11x＝22， 解得：x＝2， 把 x＝2 代入 ① ，得 4﹣y＝5， 解得：y＝﹣1， 所以方程组的解是 ； （2） ， 由 ② 得：3x﹣y＝5 ③ ， ① + ③ ×2，得 11x＝11， 解得：x＝1， 把 x＝1 代入 ① ，得 5+2y＝1， 解得：y＝﹣2， 所以方程组的解是 ． 19．（5 分）△ABC 与△A′B′C′在平面直角坐标系中的位置如图所示． （1）直接写出 A、B、C 三点的坐标，并说明△ABC 由△A′B′C′经过怎样的平移得 到？ （2）求△ABC 的面积． 解：（1）A（1，3），B（2，0），C（3，1）；△ABC 由△A'B'C'先向右平移 4 个单位， 再向上平移 2 个单位；或先向上平移 2 个单位，再向右平移 4 个单位； （2）△ABC 的面积＝2×3﹣ ﹣ ﹣ ＝2． 20．（6 分）如图，在四边形 ABCD 中，AB＝AD，∠BAD＝∠ACD＝90°，BE⊥AC 于 E． （1）求证：BE＝AC； （2）若 AB＝10，CD＝6，求四边形 ABCD 的面积． 【解答】（1）证明：∵BE⊥AC， ∴∠AEB＝90°， ∴∠ABE+∠BAE＝90°， ∵∠BAD＝90°， ∴∠DAE+∠BAE＝90°， ∴∠DAC＝∠ABE， 在△AEB 与△DCA 中， ， ∴△AEB≌△DCA（AAS）， ∴BE＝AC； （2）∵AB＝10， ∴AD＝AB＝10， 在 Rt△ACD 中，AC＝ ＝ ＝8， ∴BE＝AC＝8， ∴四边形 ABCD 的面积＝ ×AC×CD+ ×AC×BE＝ ×8×6+ ×8×8＝56． 21．（6 分）习近平在决战决胜脱贫攻坚座谈会上强调：坚决克服新冠肺炎疫情影响，坚决 夺取脱贫攻坚战全面胜利.2020 年是脱贫攻坚战最后一年，收官之年又遭遇疫情影响，各 项工作任务更重，要求更高．某地的苹果产业成为该地农民打赢脱贫攻坚战的利器，已 知该地有甲、乙两个苹果园，盛产的苹果品质相同，现两个苹果园推出了不同的销售方 案，甲苹果园：不论一次购买数量是多少，价格均为 6 元/kg；乙苹果园：一次购买数量 不超过 50kg 时，价格均为 7 元/kg，超过 50kg，则超出部分的价格按 5 元/kg 计．设某水 果店在同一个苹果园一次购买苹果的数量为 xkg（x＞0）． （1）设在甲苹果园花费 y1 元，在乙苹果园花费 y2 元，分别求 y1，y2 关于 x 的函数关系 式； （2）若该水果店计划用 360 元来购进苹果，则它在甲、乙哪个苹果园中购买苹果的数量 较多？ 解：（1）由题意可得， y1＝6x， 当 0＜x≤50，y2＝7x， 当 x＞50 时，y2＝50×7+（x﹣50）×5＝5x+100， 即 y1 关 于 x 的 函 数 关 系 式 是 y1 ＝ 6x ， y2 关 于 x 的 函 数 关 系 式 是 y2 ＝ ； （2）当 y1＝360 时，360＝6x， 解得，x＝60； 当 y2＝360 时， ∵360＞50×7， ∴360＝5x+100， 解得，x＝52； ∵60＞52， ∴该水果店在甲苹果园中购买苹果的数量较多， 答：该水果店在甲苹果园中购买苹果的数量较多． 22．（6 分）如图，在平面直角坐标系中，一次函数 y＝kx+b 的图象经过点 A（﹣2，6）， 且与 x 轴相交于点 B，与正比例函数 y＝3x 的图象相交于点 C．点 C 的横坐标为 1． （1）求 k、b 的值； （2）若点 D 是直线 AB 上一点，且满足 S△COD＝ S△BOC，求点 D 的坐标． 解：（1）当 x＝1 时，y＝3x＝3， ∴点 C 的坐标为（1，3）． 将 A（﹣2，6）、C（1，3）代入 y＝kx+b， 得： ， 解得： ． （2）当 D 在直线 OC 的下方时， ∵S△COD＝ S△BOC， ∴ ＝ ， ∴ ＝ ， 作 DE⊥x 轴于 E，CF⊥x 轴于 F， ∴DE∥CF， ∴△BDE∽△BCF， ∴ ＝ ＝ ， ∵点 C 的坐标为（1，3）． ∴CF＝3， ∴DE＝2， ∴D 的纵坐标为 2， 把 y＝2 代入 y＝﹣x+4，求得 x＝2 ∴D（2，2）， 当 D 在直线 OC 的上方时，同理，DE＝4， 把 y＝4 代入 y＝﹣x+4，求得 x＝0， ∴D（0，4）， 综上，点 D 的坐标为（2，2）或（0，4）． 23．（7 分）已知 A、B 两地之间有一条长 240 千米的公路．甲车从 A 地出发匀速开往 B 地，甲车出发两小时后，乙车从 B 地出发匀速开往 A 地，两车同时到达各自的目的地．两 车行驶的路程之和 y（千米）与甲车行驶的时间 x（时）之间的函数关系如图所示． （1）甲车的速度为 40 千米/时，a 的值为 480 ． （2）求乙车出发后，y 与 x 之间的函数关系式． （3）当甲、乙两车相距 100 千米时，求甲车行驶的时间． 解：（1）由题意可知，甲车的速度为：80÷2＝40（千米/时）； a＝40×6×2＝480， 故答案为：40；480； （2）设 y 与 x 之间的函数关系式为 y＝kx+b， 由图可知，函数图象经过（2，80），（6，480）， ∴ ，解得 ， ∴y 与 x 之间的函数关系式为 y＝100x﹣120（2≤x≤6）； （3）两车相遇前：80+100（x﹣2）＝240﹣100，解得 x＝ ； 两车相遇后：80+100（x﹣2）＝240+100，解得 x＝ ， 答：当甲、乙两车相距 100 千米时，甲车行驶的时间是 小时或 小时． 24．（10 分）（1）如图 1，已知直线 y＝﹣ x+4 与 y 轴交于 A 点，与 x 轴交于 B 点，将 线段 AB 绕点 B 顺时针旋转 90 度，得到线段 CB，求点 C 的坐标； （2）如图 2，正方形 ABCO，O 为坐标原点，B 的坐标为（﹣5，5），A，C 分别在坐 标轴上，P 是线段 BC 上动点，已知点 D 在第二象限，且是直线 y＝﹣2x﹣1 上的一点， 点 Q 是平面内任意一点，若四边形 ADPQ 是正方形，请直接写出所有符合条件的点 D 的坐标． （3）如图 3，西安铁一中滨河学校为了庆祝 2021 年元且联欢，在一块由三条小路（分 别是 x 轴和直线 AB：y＝﹣ x+4、直线 AC：y＝﹣2x﹣1）围成的三角形区域内计划搭 建一个三角形的特色场地．如图，D（4，0），△DEF 的顶点 E、F 分别在线段 AB、AC 上，且∠DEF＝90°，DE＝EF，试求出该特色场地（△DEF）的面积． 解：（1）对于直线 y＝﹣ x+4，令 y＝﹣ x+4＝0，解得 x＝8，令 x＝0，则 y＝4， 故点 A、B 的坐标分别为（0，4）、（8，0）， 过点 C 作 CH⊥x 轴于点 H， ∵∠ABO+∠CBH＝90°，∠CBH+∠BCH＝90°， ∴∠ABO＝∠BCH， ∵AB＝BC，∠BOA＝∠CHB＝90°， ∴△BOA≌△CHB（AAS）， ∴AO＝BH＝4，OB＝CH＝8， 故点 C 的坐标为（12，8）； （2）设点 D（m，﹣2m﹣1）， ① 当点 D 在 AB 下方时，如图 2， 过点 D 作 x 轴的平行线交 BC 于点 M，交 AO 于点 N， ∵四边形 PDAQ 为正方形，则 PD＝AD， 同理可得：△DMP≌△AND（AAS）， 则 MD＝AN，即 m+5＝5+2m+1，解得 m＝﹣1， 故点 D 的坐标为（﹣1，1）； ② 当点 D 在 AB 的上方时， 过点 D 作 x 轴的平行线交 y 轴于点 N，交 CB 的延长线于点 M， 同理可得：△PMD≌△DNA（AAS）， ∴AN＝BM，即﹣2m﹣1﹣5＝m+5，解得 m＝﹣ ， 故点 D 的坐标为（﹣ ， ）； 故点 D 的坐标为（﹣1，1）或（﹣ ， ）； （3）设点 E、F 的坐标分别为（m，﹣ m+4）、（n，﹣2n﹣1）， 过点 E 作 EM⊥x 轴于点 M，过点 F 作 FN⊥EM 于点 N， ∵EF＝ED， 同理可得：△FNE≌△EMD（AAS）， ∴FN＝EM，EN＝MD， 即 4﹣m＝2n﹣ m+5，m﹣n＝﹣ m+4，解得 ， 故点 E、F 的坐标分别为（2，3）、（﹣1，1）， 则 EF2＝（2+1）2+（3﹣1）2＝13， 则该特色场地（△DEF）的面积＝ EF2＝6.5．