- 2021-11-11 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学苏科九上第1章测试卷
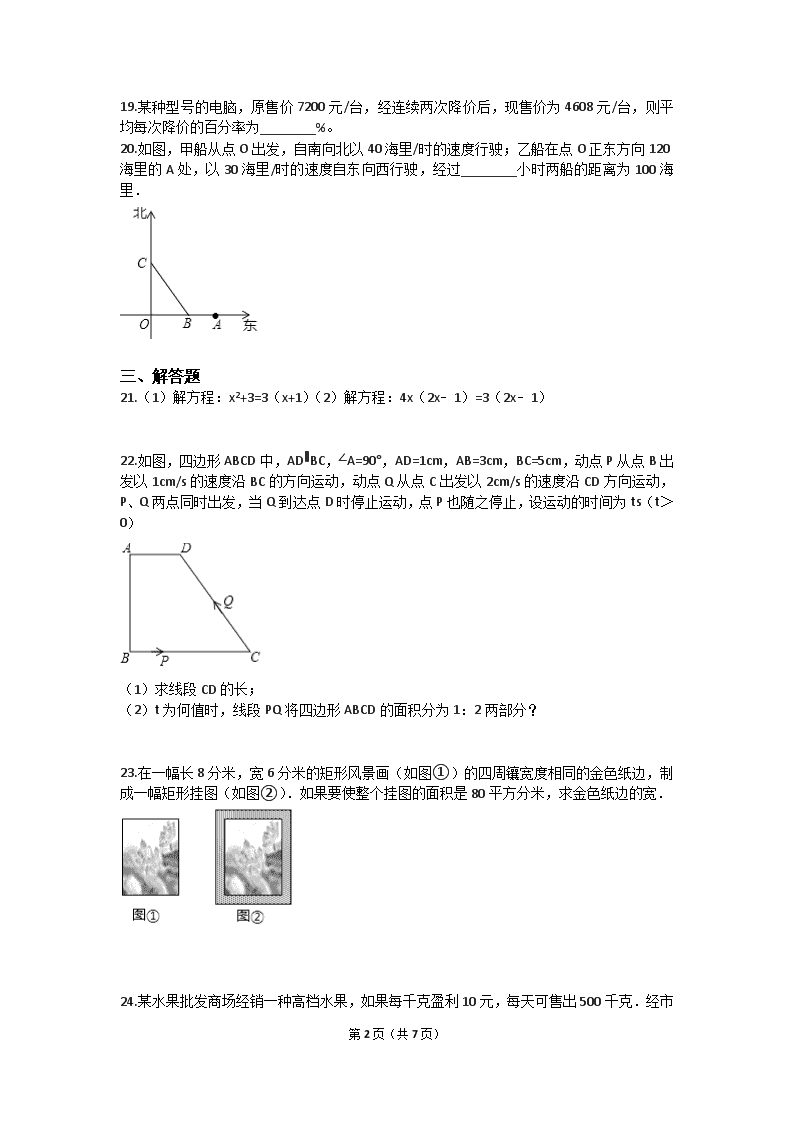
第 1页(共 7页) 单元测试卷 一、单选题 1.下列方程是一元二次方程的是( ) A.(x﹣3)x=x2+2 B. ax2+bx+c=0 C. x2=1 D. x2﹣ +2=0 2.用配方法将方程 x2+6x-11=0 变形为( ) A.(x-3)2=20 B.(x+3)2=20 C.(x+3)2=2 D.(x-3)2=2 3.方程 x2=3x 的解为( ) A. x=3 B. x=0 C. x1=0,x2=﹣3 D. x1=0,x2=3 4.若关于 x 的一元二次方程的两个根为 x1=1,x2=2,则这个方程是( ) A. x2+3x-2=0 B. x2-3x+2=0 C. x2-2x+3=0 D. x2+3x+2=0 5.三角形两边长分别为 3 和 6,第三边是方程 x2-6x+8=0 的解,则这个三角形的周长是( ) A. 11 B. 13 C. 11 或 13 D.不能确定 6.下列方程:①3x2+1=0 ② x2﹣ x+1=0 ③2x﹣ =1 ④x2﹣2xy=5 ⑤ =1 ⑥ax2+bx+c=0 其中是一元二次方程的个数( ) A. 2 B. 3 C. 4 D. 5 7.已知 a 是一元二次方程 x2﹣x﹣1=0 的根,则 2016﹣a+a2的值为( ) A. 2015 B. 2016 C. 2017 D. 0 8.用公式法解方程 5x2=6x﹣8 时,a、b、c 的值分别是( ) A. 5、6、﹣8 B. 5、﹣6、﹣8 C. 5、﹣6、8 D. 6、5、﹣8 9.已知 x=1 是一元二次方程 x2﹣ax+2=0 的一个根,则 a 的值是( ) A. 2 B. 3 C. 4 D. 5 10.方程 2x2﹣6x+3=0 较小的根为 p,方程 2x2﹣2x﹣1=0 较大的根为 q,则 p+q 等于( ) A. 3 B. 2 C. 1D. 二、填空题 11.方程 x2﹣1=0 的根为________. 12.若一元二次方程 ax2+bx+1=0 有两个相同的实数根,则 a2﹣b2+5 的最小值为________. 13.若(a+2) +4x+5=0 是关于 x 的一元二次方程,则 a 的值为________. 14.若关于 x 的方程 x2+2(k﹣1)x+k2=0 有实数根,则 k 的取值范围是________. 15.已知 m,n是方程 x2+2x﹣5=0 的两个实数根,则 m2+3mn+n2=________. 16.已知关于 x 的方程 x2﹣2x+a=0 有两个不相等的实数根,则 a 的取值范围是________. 17.已知方程 x2﹣5x+15=k2的一个根是 2,则另一个根是________. 18.如果 、 是两个不相等的实数,且满足 , ,那么代数式 =________ 第 2页(共 7页) 19.某种型号的电脑,原售价 7200 元/台,经连续两次降价后,现售价为 4608 元/台,则平 均每次降价的百分率为________%。 20.如图,甲船从点 O 出发,自南向北以 40 海里/时的速度行驶;乙船在点 O 正东方向 120 海里的 A 处,以 30 海里/时的速度自东向西行驶,经过________小时两船的距离为 100 海里. 三、解答题 21.(1)解方程:x2+3=3(x+1)(2)解方程:4x(2x﹣1)=3(2x﹣1) 22.如图,四边形 ABCD 中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点 P 从点 B 出发以 1cm/s的速度沿 BC 的方向运动,动点 Q 从点 C 出发以 2cm/s 的速度沿 CD 方向运动, P、Q 两点同时出发,当 Q 到达点 D 时停止运动,点 P 也随之停止,设运动的时间为 ts(t >0) (1)求线段 CD 的长; (2)t 为何值时,线段 PQ 将四边形 ABCD 的面积分为 1:2 两部分? 23.在一幅长 8 分米,宽 6 分米的矩形风景画(如图①)的四周镶宽度相同的金色纸边,制 成一幅矩形挂图(如图②).如果要使整个挂图的面积是 80 平方分米,求金色纸边的宽. 24.某水果批发商场经销一种高档水果,如果每千克盈利 10 元,每天可售出 500 千克.经市 场调查发现,在进货价不变的情况下,若每千克涨价 1 元,日销售量将减少 20 千克.现该 第 3页(共 7页) 商场要保证每天盈利 6000 元,同时又要使顾客得到实惠,那么每千克应涨价多少元? 25.如图,用一根长为 22cm 的铁丝分段围成一个面积为 10cm2的“田”字形的长方形铁丝框.设 宽为 x,请列出关于 x 的方程并化成一般形式. 26.如图,等边三角形 ABC 的边长为 6cm,点 P 自点 B 出发,以 1cm/s的速度向终点 C 运动; 点 Q 自点 C 出发,以 1cm/s 的速度向终点 A 运动.若 P,Q两点分别同时从 B,C 两点出发, 问经过多少时间△PCQ 的面积是 2 cm2? 27.某单位组织职工观光旅游,旅行社的收费标准是:如果人数不超过 25 人,人均旅游费用 为 100 元;如果超过 25 人,每增加 1 人,人均旅游费用降低 2 元,但人均旅游费用不得低 于 70 元.该单位按旅行社的收费标准组团,结束后,共支付给旅行社 2700 元.求该单位这 次共有多少人参加旅游? 28.水果批发市场有一种高档水果,如果每千克盈利(毛利润)10 元,每天可售出 500 千克.经 市场调查发现,在进货价不变的情况下,若每千克涨价 1 元,日销量将减少 20 千克. (Ⅰ)若以每千克能盈利 18 元的单价出售,问每天的总毛利润为多少元? (Ⅱ)现市场要保证每天总毛利润 6000 元,同时又要使顾客得到实惠,则每千克应涨价多少元? (Ⅲ)现需按毛利润的 10%交纳各种税费,人工费每日按销售量每千克支出 0.9 元,水电房租 费每日 102 元,若剩下的每天总纯利润要达到 5100 元,则每千克涨价应为多少? 第 4页(共 7页) 答案解析 一、单选题 1.【答案】C 2.【答案】B 3.【答案】D 4.【答案】C 5.【答案】B 6.【答案】A 7.【答案】C 8.【答案】C 9.【答案】B 10.【答案】B 二、填空题 11.【答案】x1=1,x2=﹣1 12.【答案】1 13.【答案】2 14.【答案】k≤ 15.【答案】-1 16.【答案】a<1 17.【答案】3 18.【答案】2026 19.【答案】20 20.【答案】2 或 三、解答题 21.【答案】解:(1)由原方程,得 x2﹣3x=0, x(x﹣3)=0, 解得 x1=0,x2=3; (2)原方程化简为:(2x﹣1)(4x﹣3)=0, 解得 x1= ,x2= . 22.【答案】(1)解:如图 1,作 DE⊥BC 于 E,则四边形 ADEB 是矩形. 第 5页(共 7页) ∴BE=AD=1,DE=AB=3, ∴EC=BC﹣BE=4, 在 Rt△DEC 中,DE2+EC2=DC2 , ∴DC= =5 厘米; (2)解:∵点 P 的速度为 1 厘米/秒,点 Q 的速度为 2 厘米/秒,运动时间为 t 秒, ∴BP=t 厘米,PC=(5﹣t)厘米,CQ=2t 厘米,QD=(5﹣2t)厘米, 且 0<t≤2.5, 作 QH⊥BC 于点 H, ∴DE∥QH, ∴∠DEC=∠QHC, ∵∠C=∠C, ∴△DEC∽△QHC, ∴ = ,即 = , ∴QH= t, ∴S△PQC= PC•QH= (5﹣t)• t=﹣ t2+3t, S 四边形 ABCD= (AD+BC)•AB= (1+5)×3=9, 分两种情况讨论: ①当 S△PQC:S 四边形 ABCD=1:3 时, ﹣ t2+3t= ×9,即 t2﹣5t+5=0, 第 6页(共 7页) 解得 t1= ,t2= (舍去); ②S△PQC:S 四边形 ABCD=2:3 时, ﹣ t2+3t= ×9,即 t2﹣5t+10=0, ∵△<0, ∴方程无解, ∴当 t 为 秒时,线段 PQ 将四边形 ABCD 的面积分为 1:2 两部分. 23.【答案】解:设金色纸边的宽为 x 分米,根据题意,得(2x+6)(2x+8)=80. 整理得:x2+7x﹣8=0, ∴(x﹣1)(x+8)=0, 解得:x1=1,x2=﹣8(不合题意,舍去). 答:金色纸边的宽为 1 分米. 24.【答案】解:设每千克水果应涨价 x 元, 依题意得方程:(500﹣20x)(10+x)=6000, 整理,得 x2﹣15x+50=0, 解这个方程,得 x1=5,x2=10. 要使顾客得到实惠,应取 x=5. 答:每千克水果应涨价 5 元 25.【答案】解:设矩形的宽为 xcm,则长为: cm, 根据题意得到:x( )=10, 化为一般形式为:3x2﹣22x+30=0. 26.【答案】解:设经过 xs△PCQ 的面积是 2 cm2 , 由题意得 (6﹣x)× x=2 解得:x1=2,x2=4, 答:经过 2s 或 4s△PCQ 的面积是 2 cm2 . 27.【答案】解:设该单位这次参加旅游的共有 x 人. ∵100×25<2700,∴x>25.[100-2(x-25)]x=2700,x2-75x+1350=0, 解得 x1=30,x2=45, 当 x=30 时,100-2(x-25)=90>70,符合题意; x=45 时,100-2(x-25)=60<70,不符合题意; 答:该单位这次参加旅游的共有 30 人. 第 7页(共 7页) 28.【答案】试题解析:解:(Ⅰ) 6120 元. (Ⅱ)设涨价 x元,则日销售量为 500-20x,根据题意得:, (10+x)(500-20x)=6000 解得 x=10 或 5, 为了使顾客得到实惠,每千克应涨价 5 元. 答:为了使顾客得到实惠,每千克应涨价 5 元. (Ⅲ)每千克涨价应为 y 元, (10+y)(500-20y)(1-10%)-0.9(500-20y)-102=5100 (y-8)²=0 y=8 答:每千克应涨价 8 元.查看更多