九年级上册青岛版数学教案3-7正多边形与圆

九年级上册青岛版数学教案3-7正多边形与圆

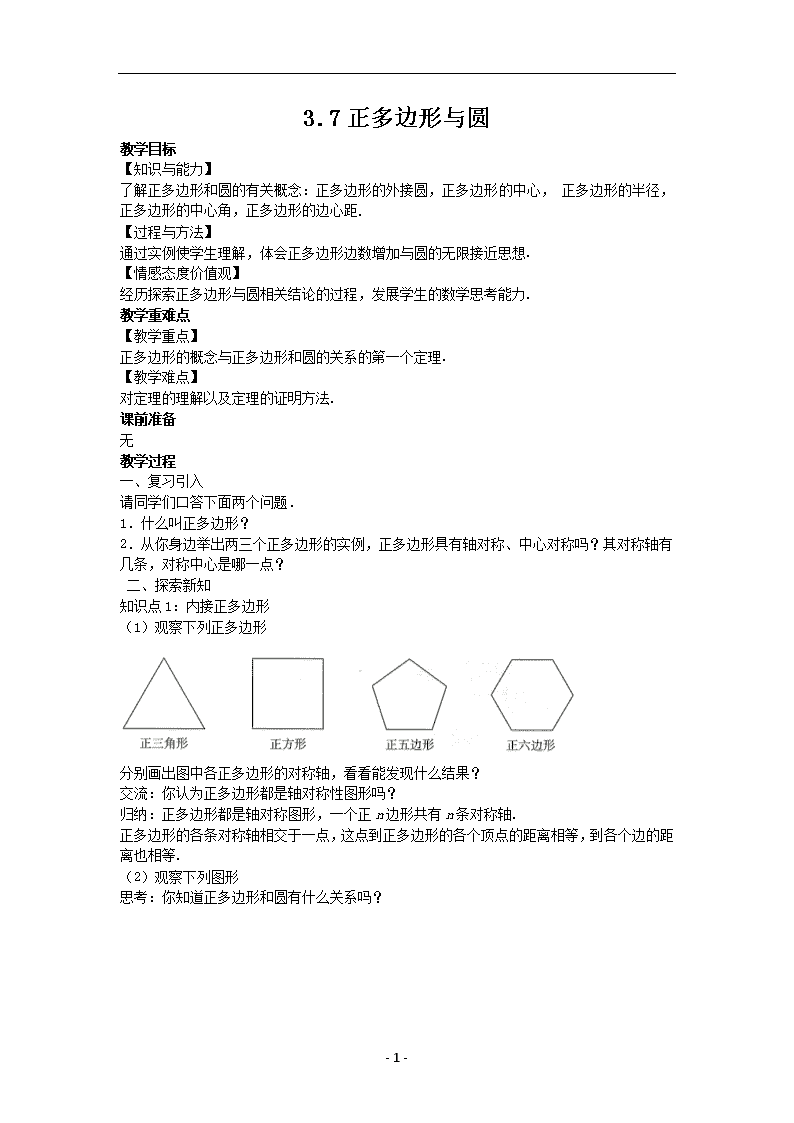
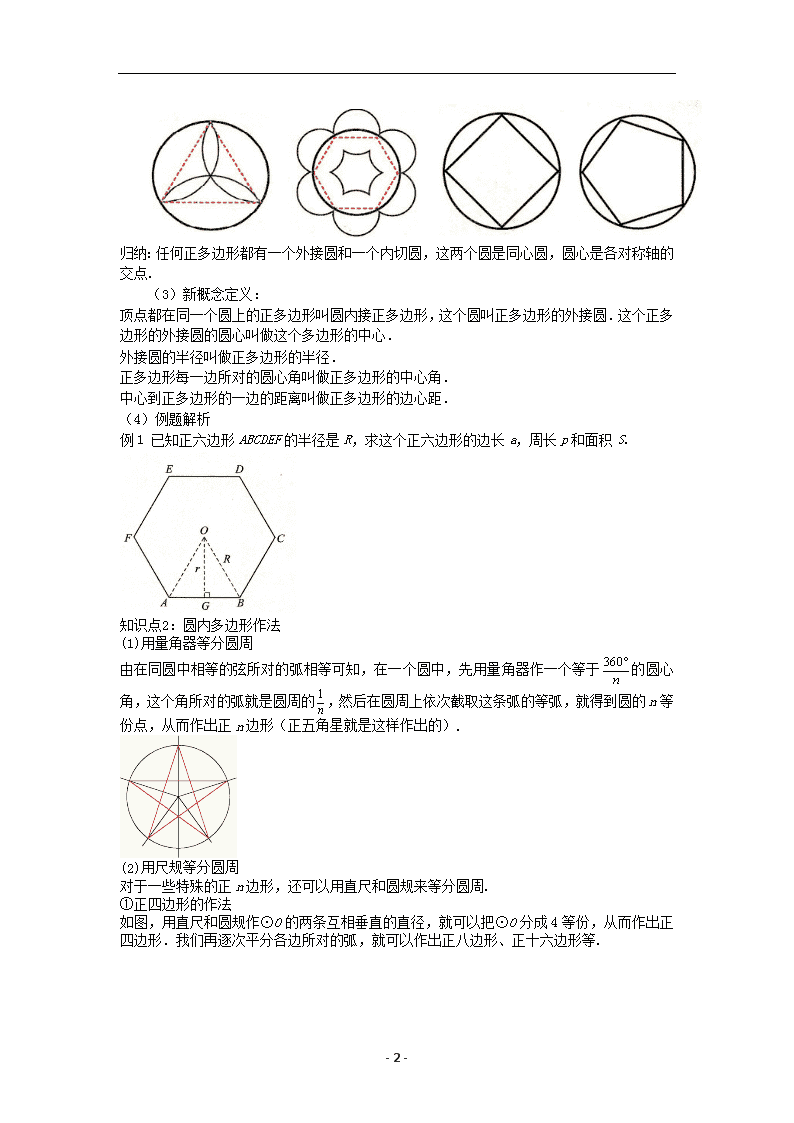
3.7正多边形与圆教学目标【知识与能力】了解正多边形和圆的有关概念：正多边形的外接圆，正多边形的中心，正多边形的半径，正多边形的中心角，正多边形的边心距.【过程与方法】通过实例使学生理解，体会正多边形边数增加与圆的无限接近思想.【情感态度价值观】经历探索正多边形与圆相关结论的过程，发展学生的数学思考能力.教学重难点【教学重点】正多边形的概念与正多边形和圆的关系的第一个定理.【教学难点】对定理的理解以及定理的证明方法.课前准备无教学过程一、复习引入请同学们口答下面两个问题．1．什么叫正多边形？2．从你身边举出两三个正多边形的实例，正多边形具有轴对称、中心对称吗？其对称轴有几条，对称中心是哪一点？二、探索新知知识点1：内接正多边形（1）观察下列正多边形分别画出图中各正多边形的对称轴，看看能发现什么结果？交流：你认为正多边形都是轴对称性图形吗？归纳：正多边形都是轴对称图形，一个正n边形共有n条对称轴.正多边形的各条对称轴相交于一点，这点到正多边形的各个顶点的距离相等，到各个边的距离也相等.（2）观察下列图形思考：你知道正多边形和圆有什么关系吗？-3- 归纳：任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆，圆心是各对称轴的交点.（3）新概念定义：顶点都在同一个圆上的正多边形叫圆内接正多边形，这个圆叫正多边形的外接圆．这个正多边形的外接圆的圆心叫做这个多边形的中心．外接圆的半径叫做正多边形的半径．正多边形每一边所对的圆心角叫做正多边形的中心角．中心到正多边形的一边的距离叫做正多边形的边心距．（4）例题解析 例1已知正六边形ABCDEF的半径是R，求这个正六边形的边长a，周长p和面积S.知识点2：圆内多边形作法(1)用量角器等分圆周由在同圆中相等的弦所对的弧相等可知，在一个圆中，先用量角器作一个等于的圆心角，这个角所对的弧就是圆周的，然后在圆周上依次截取这条弧的等弧，就得到圆的n等份点，从而作出正n边形（正五角星就是这样作出的）.(2)用尺规等分圆周对于一些特殊的正n边形，还可以用直尺和圆规来等分圆周.①正四边形的作法如图，用直尺和圆规作⊙O的两条互相垂直的直径，就可以把⊙O分成4等份，从而作出正四边形．我们再逐次平分各边所对的弧，就可以作出正八边形、正十六边形等.-3- ②正六边形的作法如图(1)，设⊙O的半径为R，通常先作出⊙O的一条自径AB，然后分别以点A,B为圆心、R为半径作弧，与⊙O交于点C,D,E,F，从而得到⊙O的6等份点，作出正六边形．如果再逐次等分各边所对的弧，就可作出正十二边形、正二十四边形等．我们可以连接6等份圆周的相间两个点，得到正三角形，如图(2).(3)例题解析例2用直尺和圆规作圆的内接正方形.例3用直尺和圆规作圆的内接正六边形.三、归纳小结（学生小结，老师点评）1．正多边和圆的有关概念：正多边形的中心，正多边形的半径，正多边形的中心角，正多边的边心距．2．正多边形的半径、正多边形的中心角、边长、正多边的边心距之间的等量关系．-3-