人教版九年级上册数学同步课件-第24章-24点和圆的位置关系
第二十四章圆24.2点和圆、直线和圆的位置关系24.2.1点和圆的位置关系
问题我国射击运动员在巴西奥运会上获奖牌,为我国赢得荣誉.如图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不相同)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?新课导入
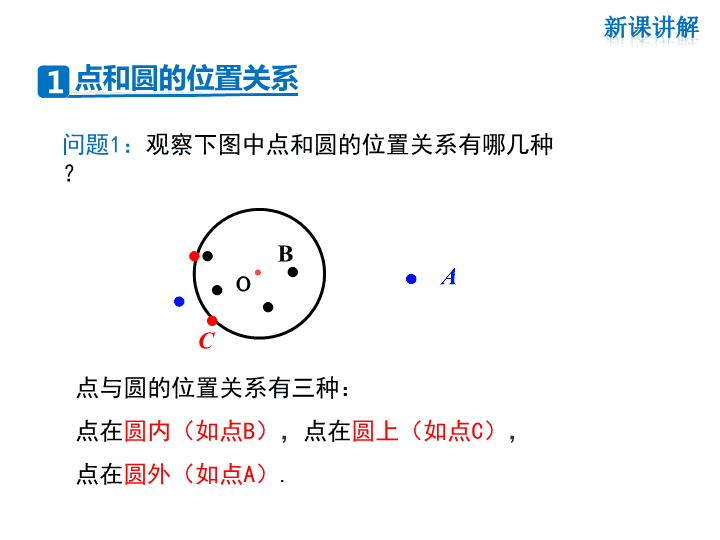
问题1:观察下图中点和圆的位置关系有哪几种?.o.C....B..A.点与圆的位置关系有三种:点在圆内(如点B),点在圆上(如点C),点在圆外(如点A).点和圆的位置关系新课讲解1
问题2:设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?点P在⊙O内点P在⊙O上点P在⊙O外dddrpdprdPrd<rr=>r反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?新课讲解
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在;点B在;点C在.练一练:圆内圆上圆外2.圆心为O的两个同心圆,半径分别为1和2,若OP=,则点P在()A.在大圆内B.在小圆内C.小圆外D.大圆内,小圆外oD新课讲解
★点和圆的位置关系rpdprdPrdRrP点P在⊙O内d
r点P在圆环内r≤d≤R数形结合:位置关系数量关系要点归纳
问题1:平面上有一点A,经过已知A点的圆有几个?圆心在哪里?●O●A●O●O●O●O能画出无数个圆,圆心为点A以外任意一点,半径为这点与点A的距离.过不在同一直线上的三个点作圆新课讲解2
回顾线段垂直平分线的尺规作图的方法1.分别以点A和B为圆心,以大于二分之一AB的长为半径作弧,两弧相交于点M和N;2.作直线MN.NMAB新课讲解
合作探究问题2:过两个点能不能确定一个圆?●O●O●O●OAB能画出无数个圆,圆心都在线段AB的垂直平分线上。新课讲解
有且只有位置关系定理:不在同一直线上的三个点确定一个圆.问题3:过不在同一直线上的三点能不能确定一个圆?ABCDEGF●o经过B,C两点的圆的圆心在线段BC的垂直平分线上.经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.经过A,B两点的圆的圆心在线段AB的垂直平分线上.新课讲解
1.外接圆⊙O叫做△ABC的________,△ABC叫做⊙O的____________.到三角形三个顶点的距离相等.2.三角形的外心:定义:●OABC外接圆内接三角形三角形外接圆的圆心叫做三角形的外心.作图:三角形三边中垂线的交点.性质:★圆内接三角形有关定义新课讲解
判一判:下列说法是否正确?(1)任意的一个三角形一定有一个外接圆()(2)任意一个圆有且只有一个内接三角形()(3)经过三点一定可以确定一个圆()(4)三角形的外心到三角形各顶点的距离相等()√××√新课讲解
画一画:分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.1.锐角三角形的外心位于三角形内,2.直角三角形的外心位于直角三角形斜边的中点,3.钝角三角形的外心位于三角形外.ABC●OABCCAB┐●O●O新课讲解
思考:经过同一条直线上的三个点能作出一个圆吗?l1l2ABCP如图,假设过同一条直线l上三点A、B、C可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.新课讲解反证法3
★反证法的定义先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.★反证法的一般步骤骤假设命题的结论不成立;从这个假设出发,经过推理,得出矛盾;由矛盾判定假设不正确,从而肯定命题的结论正确.要点归纳
1.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A;点C在⊙A;点D在⊙A.上外上2.⊙O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为()A.点P在⊙O内B.点P在⊙O上C.点P在⊙O外D.点P在⊙O上或⊙O外B3.直角三角形的两条直角边分别是6、8,则这个直角三角形外接圆的半径是.5随堂练习
1·2cm3cm4.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.O随堂练习
如图,是一块圆形镜片破碎后的部分残片,试找出它的圆心.ABCO圆心一定在弦的垂直平分线上.拓展提升
点与圆的位置关系点在圆外点在圆上点在圆内d>rd=rd
查看更多