初中数学中考总复习课件PPT：第8课时　一元二次方程及其应用

初中数学中考总复习课件PPT：第8课时　一元二次方程及其应用

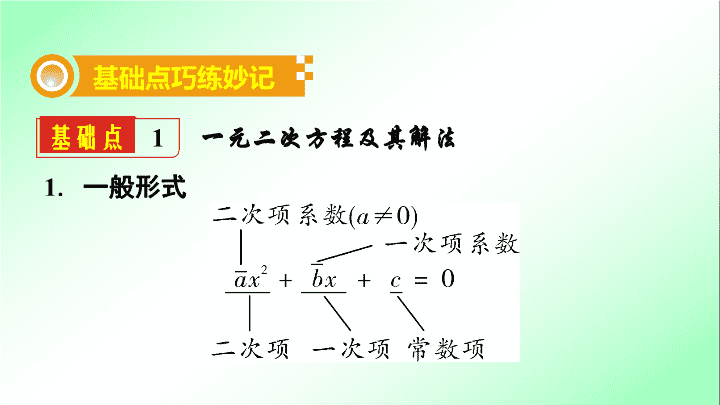
第一部分 夯实基础　提分多 第 二 单元 方程（组）与不等式（组） 第 8 课时　一元二次方程及其应用 基础点 1 一元二次方程及其解法 基础点巧练妙记 1 ． 一般形式 2. 一元二次方程必须具备三个条件： (1) 必须是 ① ______ 方程； (2) 必须只含有 ② ________ 未知数； (3) 所含未知数的最高次数是 ③ ________ ． 整式 1 个 2 【温馨提示】 一元二次方程的一般形式中要注意 a ≠ 0. 当 a ＝ 0 时，不含有二次项，即不是一元二次方程． 3. 一元二次方程的解法 (1) 公式法： 适用于所有一元二次方程． 需满足两个条件： a . 先将方程化为 ax 2 ＋ bx ＋ c ＝ 0(a≠0) 的形式； b .b 2 － 4ac≥0 ，求根公式： x ＝ ④ ____________ ． (2) 直接开平方法 ：适用于 x 2 － c ＝ 0( c ＞ 0) 和 ( x ＋ a ) 2 ＝ b ( b ≥0) 的形式． (3) 因式分解法 ：适用于方程的右边化为 0 后，方程的左边可以提出含有 x 的公因式． (4) 配方法 ：适用于 x 2 ＋ px ＋ q ＝ 0 的形式，其中 x 2 ＋ px ＋ q 不能进行因式分解，配方后直接开平方进行求解． 步骤：将二次项系数化为 1 ；移项，使方程左边只含有 二次项和一次项，右边为 0 ；方程两边同时加上一次项系数一半的平方；化为完全平方式的形式． 练 提 分 必 1 ．方程 ( x ＋ 3) 2 ＝ 4 的解是 ( 　　 ) A ． x 1 ＝－ 1 ， x 2 ＝ 5 　　　　 B ． x 1 ＝ 1 ， x 2 ＝－ 5 C ． x 1 ＝－ 1 ， x 2 ＝－ 5 D ． x 1 ＝ 1 ， x 2 ＝ 5 C 练 提 分 必 2 ．方程 x 2 － 4 x － 12 ＝ 0 的两个根为 ( 　　 ) A ． x 1 ＝－ 2 ， x 2 ＝ 6 B ． x 1 ＝－ 6 ， x 2 ＝ 2 C ． x 1 ＝－ 3 ， x 2 ＝ 4 D ． x 1 ＝－ 4 ， x 2 ＝ 3 3 ．解方程： 5 x 2 － 3 x ＝ x ＋ 1. x 1 ＝ ， x 2 ＝ 1 A 4 失 分 点 解一元二次方程 “ 丢根 ” 解方程： x ( x － 1) ＝ 2( x － 1) 2 . 【自主解答】           解： x ( x － 1) ＝ 2( x － 1) 2 ， 去括号，得 x 2 － x ＝ 2 x 2 － 4 x ＋ 2 ， 移项、合并同类项，得 x 2 － 3 x ＋ 2 ＝ 0 ， 系数化为 1 ，得 ( x － 1)( x － 2) ＝ 0 ， 解得 x 1 ＝ 1 ， x 2 ＝ 2. 【名师点拨】 对于左右两边含有相同因式的一元二次方程，应将方程化为一般式后再求解 ( 或将方程变为等号一边为 0 ，另一边含未知数的式子，利用因式分解法求解 ) ，切勿直接约去公因式而丢根． 4 失 分 点           基础点 2 1 ． 根的判别式 (1) b 2 － 4 ac ⑤ ______0⇔ 方程有两个不相等的实数根； (2) b 2 － 4 ac ＝ 0⇔ 方程有 ⑥ _________ 的实数根； (3) b 2 － 4 ac ⑦ ______0⇔ 方程无实数根． > 两个相等 < 一元二次方程根的判别式及根与系数关系 4 ．一元二次方程 x 2 － 4 x ＋ 4 ＝ 0 的根的情况是 __________________ ． 5 ．一元二次方程 ax 2 ＋ 2 x ＋ 1 ＝ 0 有解，则 a 的取值范围是 __________ ． 练 提 分 必 有两个相等的实数根 a ≤1 且 a ≠0 【温馨提示】 根的判别式的两个作用： (1) 不解方程，直接判断一元二次方程根的情况； (2) 根据方程根的情况，确定某个未知系数的值 ( 或范围 ) ． 2 ．根与系数的关系 若 x 1 、 x 2 是一元二次方程 ax 2 ＋ bx ＋ c ＝ 0( a ≠0) 的两个实数根，则 x 1 ＋ x 2 ＝ ， x 1 · x 2 ＝ . 应用：常用根与系数关系解决以下问题： ①已知方程及方程一个根，求另一个根及未知数； ②不解方程，求关于根的式子的值，如求 x 1 ＋ x 2 ， x 1 · x 2 ； ③由给出的两根满足的条件，确定字母的取值范围． 【 温馨提示 】 利用根与系数的关系解题的前提是方程的两根存在，即注意根的判别式 b 2 － 4 ac ≥0. 6 ．已知 x 1 ， x 2 是一元二次方程 x 2 － 2 x － 1 ＝ 0 的两根，则 ________ ． 7 ．若关于 x 的方程 x 2 ＋ 3 x ＋ a ＝ 0 有一个根为－ 1 ，则另一个根为 ________ ． 练 提 分 必 － 2 － 2 基础点 3 一元二次方程 根的 实际应用 增长率问题：设基数为 a ，平均增长率为 x ，则一次增长后的值为 ⑧ ________ ，二次增长后的值为 ⑨ ________ ； 下降率问题 ：若基数为 a ，平均下降率为 x ，则一次降低后的值为⑩________，二次降低后的值为⑪________． a (1 ＋ x ) a (1 ＋ x ) 2 a (1- x ) a (1- x ) 2 8. 政府近几年大力降低药品价格，希望使广大人民群众看得起病吃得起药．某种针剂的单价由 100 元经过两次降价，降至 64 元，设平均每次下降的百分率为 x ，则可列方程为 _______________ ． 9. 某商厦二月份的销售额为 100 万元，三月份的销售额下降了 20% ，该商厦赶快改进经营措施，销售额开始稳步上升，五月份销售额达到了 135.2 万元，设四、五月份的 练 提 分 必 100(1 － x) 2 ＝ 64 重难点精讲优练 类型 1 一元二次方程根的判别式 例 1 已知关于 x 的一元二次方程 ( m － 2) x 2 ＋ 2 mx ＋ m ＋ 3 ＝ 0 ，当方程满足以下条件时，分别求出 m 的取值范围． (1) 方程有两个相等的实数根； (2) 方程有两个不相等的实数根； (3) 方程无实数根． 平均增长率为 x ，则可列方程为 ________________________ ． 10. 某超市 1 月份的营业额为 200 万元，第一季度营业额为 1000 万元，若平均每月增长率相同，求该平均增长率． 练 提 分 必 100(1 － 20%)(1 ＋ x ) 2 ＝ 135.2 平均增长率为 56%. 且 m － 2≠0 ， 解得 m ＝ 6 ； (2)∵ 方程有两个不相等的实数根， ∴ b 2 － 4 ac ＝ (2 m ) 2 － 4( m － 2)( m ＋ 3) ＝－ 4 m ＋ 24 ＞ 0 ， 且 m － 2≠0 ， 解得 m ＜ 6 且 m ≠2 ； (3)∵ 方程无实数根， ∴ b 2 － 4 ac ＝ (2 m ) 2 － 4( m － 2)( m ＋ 3) ＝－ 4 m ＋ 24 ＜ 0 ，且 m － 2≠0 ，解得 m ＞ 6. 练习 1 已知关于 x 的方程 kx 2 ＋ (2 k ＋ 1) x ＋ ( k － 1) ＝ 0 有实数根，则 k 的取值范围为 ( 　　 ) A. k ≥ － B. k ＞－ C. k ≥ － 且 k ≠0 D. k ＜－ 【解析】当 k ≠0 时，方程为一元二次方程，∵方程有实数根，∴ b 2 － 4 ac ＝ (2 k ＋ 1) 2 － 4 k ( k － 1) ＝ 8 k ＋ 1≥0 ，且 k ≠0 ，解得 k ≥ － 且 k ≠0 ，当 k ＝ 0 时，方程为 x － 1 ＝ 0 ， 解得 x ＝ 1 ，满足题意，综上， k ≥－ . 类型 2 一元二次方程根与系数的关系 例 2 已知一元二次方程 2 x 2 － x － 2 ＝ 0 的两根是 x 1 ， x 2 ，求下列代数式的值． (1) ； (2) ； (3)( x 1 － x 2 ) 2 ； (4)( x 1 ＋ 1)( x 2 ＋ 1) ； (5)| x 1 － x 2 | ； (6) x 2 ＋ ； (7) ； (8) . 解： (1)∵ 方程有两个实数根 x 1 ， x 2 ， ∴ x 1 ＋ x 2 ＝ ， x 1 x 2 ＝－ 1 ， ∴原式＝ ( x 1 ＋ x 2 ) 2 － 2 x 1 x 2 ＝ ＋ 2 ＝ ； (2) 原式＝ ＝ ； (3) 原式＝ － 2 x 1 x 2 ＋ ＝ ( x 1 ＋ x 2 ) 2 － 4 x 1 x 2 ＝ ； (4) 原式＝ x 1 ＋ x 2 ＋ x 1 x 2 ＋ 1 ＝ ＋ ( － 1) ＋ 1 ＝ ； (5) 原式 (6) 原式 (7) 原式 (8) 原式 练习 2 　 设 x 1 、 x 2 是方程 x 2 － 4 x ＋ m ＝ 0 的两个根，且 x 1 ＋ x 2 － x 1 x 2 ＝ 1 ，则 x 1 ＋ x 2 ＝ ________ ， m ＝ ________ ． 4 3 变式拓展 　 已知关于 x 的两个方程 ① ax 2 ＋ bx ＋ c ＝ 0 与 ② ax 2 ＋ ( b － a ) x ＋ c － b ＝ 0 ，其系数都满足 a ＞ b ＞ c ，方程 ① 有两个异号实数根． (1) 证明：方程 ② 一定有两个不相等的实数根； (2) 若 1 是方程 ① 的一个根，方程 ② 的两个根分别为 x 1 、 x 2 ，令 k ＝ ，问：是否存在实数 k ，使 ＝ 9 ？如果存在，求出 k 的值；如果不存在，请说明理由． （ 1 ）证明 ：方程 ② 中， Δ ＝ ( b － a ) 2 － 4a(c － b) ＝ ( a ＋ b ) 2 － 4 ac ∵方程 ① 有两个异号实数根， ∴ a ≠ 0 ，且 ＜ 0 ， ∴ ac ＜ 0 ， ∴ Δ ＝ ( a ＋ b ) 2 － 4 ac ＞ 0 ， ∴方程 ② 一定有两个不相等的实数根； (2) 解： ∵ x 1 、 x 2 是方程 ② 的两个根，∴ x 1 ＋ x 2 ＝ ， x 1 x 2 ＝ ， ∵ 1 是方程 ① 的一个根， ∴ a ＋ b ＋ c ＝ 0 ， ∴－ b ＝ a ＋ c ， ∴ a ≠ 0 ， k ＝ ＜ 0 ， ∴ k ＝ . ∴ ＝ (1 ＋ 2 k )(2 ＋ k ) ＝ 2 k 2 ＋ 5 k ＋ 2 ＝ 9 ， 化简得 2 k 2 ＋ 5 k － 7 ＝ 0 ，解得 k 1 ＝ ， k 2 ＝ 1 ， ∵方程 ① 有两个异号实数根， 一元二次方程中利用根与系数的关系求代数式的值常用到以下几个关系式： 导 方 法 指 导 方 法 指