中考数学复习冲刺专项训练精讲：反比例函数教学课件（初三数学章节复习课件）

中考数学复习冲刺专项训练精讲：反比例函数教学课件（初三数学章节复习课件）

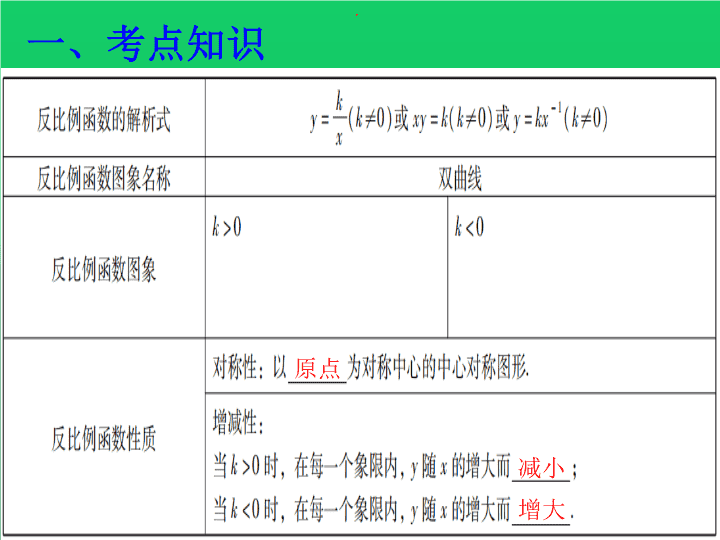
第三章　函数 　反比例函数 中考数学复习冲刺专项训练精讲 一、考点知识 ， 原点 减小 增大 【例1】已知反比例函数 ，当x＝2时，y＝－2. (1)求此反比例函数解析式； (2)当2≤x≤4时，求函数值y的取值范围． 【考点1】求反比例函数解析式，反比例函数性质 二、例题与变式 解：（1） （2）－2≤y≤－1 5 my x  4y x   【变式1】已知反比例函数过点(1，2)． (1)求此函数解析式并画出图象； (2)根据图象求出当y≤1时，x的取值范围． 解：（1） （2）图略，x≥2或x<0 2y x  【考点2】一次函数与反比例函数 【例2】已知一次函数与反比例函数的图象交于点 P(－3，m)，Q(2，－3)．(1)求这两个函数的函数关 系式； (2)在给定的平面直角坐标系(如图)中，画出这两个 函数的大致图象； (3)当x为何值时，一次函数的值大于反比例函数的 值？ 解：（1） ,y=－x－1 （2）图略 （3）x<－3或03或－30)的图象经过点C，交AB于点D. 已知AB＝4，BC＝ (1)若OA＝4，求k的值； (2)连接OC，若BD＝BC，求OC的长． 解：（1）如图，作CE⊥AB，垂足为E. ∵AC＝BC，AB＝4，∴AE＝BE＝2. 在Rt△BCE中，BC＝ ，BE＝2， ∴CE＝ .∵OA＝4， ∴点C的坐标为 ． ∵点C在 的图象上， ∴k＝5. ky x  5 2 5 23 2 ky x  5( 2)2 ， 【变式2】如图，在平面直角坐标系中，▱ OABC的顶点A， C的坐标分别为A(2，0)，C(－1，2)，反比例函数 (k≠0)的图象经过点B. (1)求k的值； (2)将▱ OABC沿x轴翻折，点C落在点C′处，判断点C′是否在反比例 函数 (k≠0)的图象上，请通过计算说明理由． 解：(1)∵四边形OABC为平行四边形， ∴BC∥OA. ∵A（2,0) ，C（－1,2） ， ∴B（1,2）．将B（1,2）代入反比例函数解析式， 得2＝ .∴k＝2. ky x  ky x  1 k A组 1．给出下列函数：①y＝－3x＋2；② ；③y＝2x2； ④y＝3x，上述函数中符合条作“当x＞1时，函数值y随自变 量x增大而增大”的是________． 三、过关训练 2．如图，A，C是函数 的图象上的任意两点，过点A作x轴 的垂线，垂足为点B，过点C作y轴的垂线，垂足为点D，连接OA， OC，设Rt△AOB的面积为S1，Rt△COD的面积为S2，则(　　) A．S1＞S2 B．S1＜S2 C．S1＝S2 D．S1和S2的大小关系不能确定 ③④ 3y x  ky x  C 3．函数 的图象与直线y＝x没有交点，那么k的取 值范围是(　　) A．k＞1　　　　　B．k＜1 C．k＞－1 D．k＜－1 1 ky x  A B组 4．已知一次函数y＝kx＋b的图象经过点A(0，1)和点B (a，－3a), a＜0，且点B在反比例函数 的图象上． (1)求a的值和一次函数的解析式． (2)如果P(m, y1)，Q(m＋1, y2)是这个一次函数图象上的两点， 试比较y1与y2的大小． 解：（1）a=－1, y=－2x+1 （2）y1>y2 3y x   4 1 12y y xx     ， 5．如图，一次函数y＝kx＋b的图象与坐标轴分别交于A， B两点，与反比例函数 的图象在第二象限的交点 为C，CD⊥x轴，垂足为D，若OB＝2，OD＝4，△AOB的 面积为1. (1)求一次函数与反比例函数的解析式； (2)根据图象，直接写出当x<0时，kx＋b－ ＞0的解集． my x  m x 解：（1） （2）x<－4 C组 6．如图，四边形OABC是面积为4的正方形，函数 (x＞0)的图象经过点B. (1)求k的值； (2)将正方形OABC分别沿直线AB，BC翻折，得到正方形MABC′， NA′BC.设线段MC′，NA′分别与函数 (x＞0)的图象交于点E， F，求线段EF所在直线的解析式． 解： (1)∵四边形OABC是面积为4的正方形， ∴OA＝OC＝2. ∴点B坐标为（2，2)． ∴k＝xy＝2×2＝4. ky x  ky x  (2)∵正方形MABC′，NA′BC是由正方形OABC翻折所得， ∴ON＝OM＝2OA＝4. ∴点E横坐标为4，点F纵坐标为4. ∵点E，F在函数 的图象上，∴E（4，1） ，F（1，4）． 设直线EF解析式为y＝mx＋n， 将E，F两点坐标代入， 得 4m+n=1, 解得 m=－1, m+n=4. n=5. ∴直线EF的解析式为y＝－x＋5. 4y x 