2019-2020学年浙江省绍兴市越城区八年级（下）期末数学试卷 解析版

2019-2020学年浙江省绍兴市越城区八年级（下）期末数学试卷 解析版

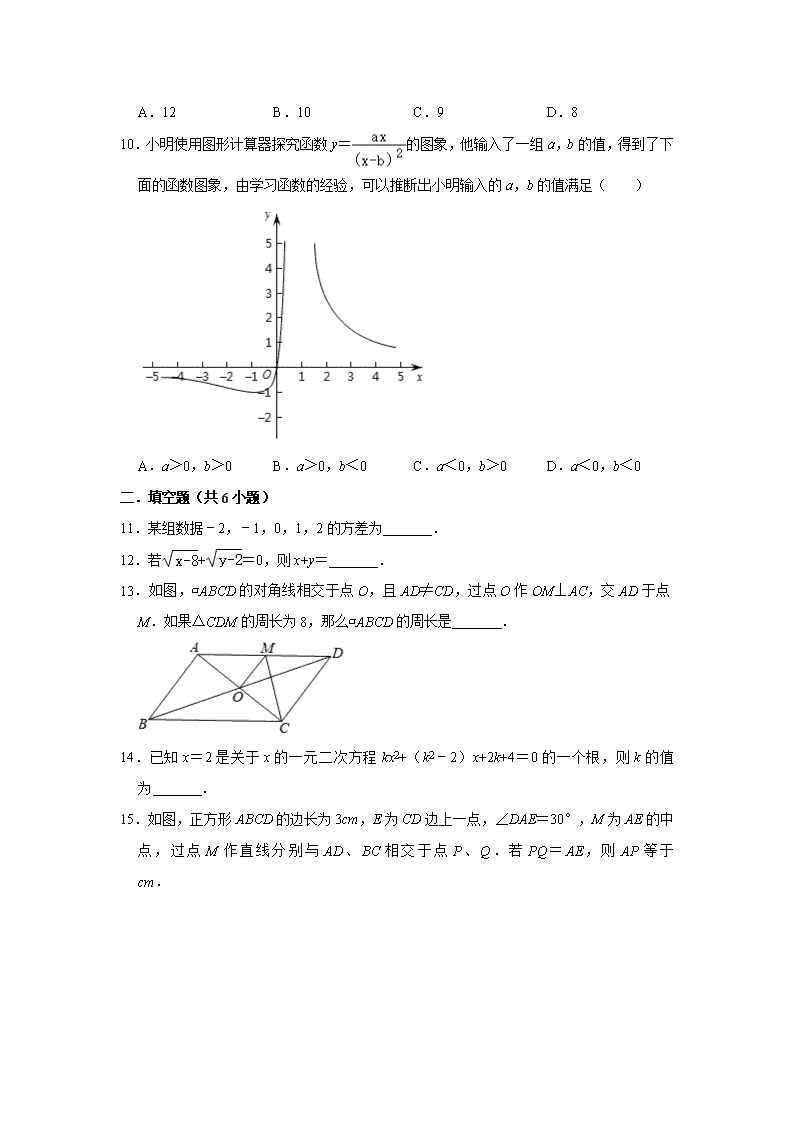
‎2019-2020学年浙江省绍兴市越城区八年级（下）期末数学试卷 一．选择题（共10小题）‎ ‎1．下列各式中，化简后能与合并的是（　　）‎ A． B． C． D．‎ ‎2．一元二次方程x2﹣2x＝0的两根分别为x1和x2，则x1x2为（　　）‎ A．﹣2 B．‎1 ‎C．2 D．0‎ ‎3．已知反比例函数的图象过点M（﹣1，2），则此反比例函数的表达式为（　　）‎ A．y＝ B．y＝﹣ C．y＝ D．y＝﹣‎ ‎4．有一组数椐：3，4，5，6，6，则下列四个结论中正确的是（　　）‎ A．这组数据的平均数、众数、中位数分别是4.8，6，6 ‎ B．这組数据的平均数、众数、中位数分别是5，5，5 ‎ C．这组数据的平均数、众数、中位数分别是4.8，6，5 ‎ D．这组数据的平均数、众数、中位数分别是5，6，6‎ ‎5．已知▱ABCD中，∠A+∠C＝80°，则∠B的度数为（　　）‎ A．80° B．100° C．120° D．140°‎ ‎6．估算的值（　　）‎ A．在1和2之间 B．在2和3之间 C．在3和4之间 D．在4和5之间 ‎7．若a，b，c满足，则关于x的方程ax2+bx+c＝0（a≠0）的解是（　　）‎ A．1，0 B．﹣1，‎0 ‎C．1，﹣1 D．无实数根 ‎8．从下列条件中选择一个条件添加后，还不能判定平行四边形ABCD是菱形，则这个条件是（　　）‎ A．AC⊥BD B．AC＝BD C．AB＝BC D．AD＝CD ‎9．如图，已知双曲线y＝（k＜0）经过Rt△OAB斜边OA的中点D，且与直角边AB相交于点C，若点A的坐标为（﹣6，4），则△AOC的面积为（　　）‎ A．12 B．‎10 ‎C．9 D．8‎ ‎10．小明使用图形计算器探究函数y＝的图象，他输入了一组a，b的值，得到了下面的函数图象，由学习函数的经验，可以推断出小明输入的a，b的值满足（　　）‎ A．a＞0，b＞0 B．a＞0，b＜‎0 ‎C．a＜0，b＞0 D．a＜0，b＜0‎ 二．填空题（共6小题）‎ ‎11．某组数据﹣2，﹣1，0，1，2的方差为　 　．‎ ‎12．若+＝0，则x+y＝　 　．‎ ‎13．如图，▱ABCD的对角线相交于点O，且AD≠CD，过点O作OM⊥AC，交AD于点M．如果△CDM的周长为8，那么▱ABCD的周长是　 　．‎ ‎14．已知x＝2是关于x的一元二次方程kx2+（k2﹣2）x+2k+4＝0的一个根，则k的值为　 　．‎ ‎15．如图，正方形ABCD的边长为‎3cm，E为CD边上一点，∠DAE＝30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q．若PQ＝AE，则AP等于　 　cm．‎ ‎16．如图，曲线l是由函数y＝在第一象限内的图象绕坐标原点O逆时针旋转45°得到的，过点A（﹣4，4），B（2，2）的直线与曲线l相交于点M、N，则△OMN的面积为　 　．‎ 三．解答题（共8小题）‎ ‎17．计算：‎ ‎（1）4﹣+；‎ ‎（2）（3﹣）．‎ ‎18．选择合适的方法解一元二次方程：‎ ‎（1）4（x﹣5）2＝16；‎ ‎（2）（x+3）（x﹣1）＝5．‎ ‎19．如图，在▱ABCD中，∠ABD＝90°，延长AB至点E，使BE＝AB，连接CE．求证：四边形BECD是矩形．‎ ‎20．已知图中的曲线是反比例函数y＝（m为常数）图象的一支．‎ ‎（1）根据图象位置，求m的取值范围；‎ ‎（2）若该函数的图象任取一点A，过A点作x轴的垂线，垂足为B，当△OAB 的面积为4时，求m的值．‎ ‎21．某商场经理对某一品牌旅游鞋近一个月的销售情况进行统计后，绘制了如下统计表与条形图：‎ 尺码（码）‎ 数量（双）‎ 百分比（%）‎ ‎36‎ ‎60‎ ‎30‎ ‎37‎ ‎30‎ ‎15‎ ‎38‎ a b ‎39‎ ‎40‎ ‎20‎ ‎40‎ c ‎5‎ ‎41‎ ‎10‎ ‎5‎ ‎（1）写出表中a，b，c的值；‎ ‎（2）补全条形图；‎ ‎（3）商场经理准备购进同一品牌的旅游鞋1500双，请根据市场实际情况估计他应该购进‎38码的鞋多少双？‎ ‎22．已知关于x的方程mx2+（‎3m+1）x+3＝0．‎ ‎（1）求证：不论m为任何实数，此方程总有实数根；‎ ‎（2）若方程mx2+（‎3m+1）x+3＝0有两个不同的整数根，且m为正整数，求m的值．‎ ‎23．如图，在△ABC中，∠ACB＝90°，∠CAB＝30°，以线段AB为边向外作等边△ABD，点E是线段AB的中点，连接CE并延长交线段AD于点F．‎ ‎（1）求证：四边形BCFD为平行四边形；‎ ‎（2）若AB＝6，求平行四边形BCFD的面积．‎ ‎24．已知点A、B分别是x轴、y轴上的动点，点C、D是某个函数图象上的点，当四边形ABCD（A、B、C、D各点依次排列）为正方形时，称这个正方形为此函数图象的伴侣正方形．例如：如图，正方形ABCD是一次函数y＝x+1图象的其中一个伴侣正方形．‎ ‎（1）若某函数是一次函数y＝x+1，求它的图象的所有伴侣正方形的边长；‎ ‎（2）若某函数是反比例函数，它的图象的伴侣正方形为ABCD，点D（2，m）（m＜2）在反比例函数图象上，求m的值及反比例函数解析式．‎ ‎ ‎ 参考答案与试题解析 一．选择题（共10小题）‎ ‎1．下列各式中，化简后能与合并的是（　　）‎ A． B． C． D．‎ ‎【分析】先化成最简二次根式，再根据同类二次根式的定义判断即可．‎ ‎【解答】解：A、＝2，不能与合并；‎ B、＝2，能与合并；‎ C、＝，不能与合并；‎ D、＝，不能与合并；‎ 故选：B．‎ ‎2．一元二次方程x2﹣2x＝0的两根分别为x1和x2，则x1x2为（　　）‎ A．﹣2 B．‎1 ‎C．2 D．0‎ ‎【分析】根据根与系数的关系可得出x1x2＝0，此题得解．‎ ‎【解答】解：∵一元二次方程x2﹣2x＝0的两根分别为x1和x2，‎ ‎∴x1x2＝0．‎ 故选：D．‎ ‎3．已知反比例函数的图象过点M（﹣1，2），则此反比例函数的表达式为（　　）‎ A．y＝ B．y＝﹣ C．y＝ D．y＝﹣‎ ‎【分析】函数经过一定点，将此点坐标代入函数解析式（k≠0），即可求得k的值．‎ ‎【解答】解：设反比例函数的解析式为（k≠0）．‎ ‎∵该函数的图象过点M（﹣1，2），‎ ‎∴2＝，‎ 得k＝﹣2．‎ ‎∴反比例函数解析式为y＝﹣．‎ 故选：B．‎ ‎4．有一组数椐：3，4，5，6，6，则下列四个结论中正确的是（　　）‎ A．这组数据的平均数、众数、中位数分别是4.8，6，6 ‎ B．这組数据的平均数、众数、中位数分别是5，5，5 ‎ C．这组数据的平均数、众数、中位数分别是4.8，6，5 ‎ D．这组数据的平均数、众数、中位数分别是5，6，6‎ ‎【分析】要求平均数只要求出数据之和再除以总个数即可；对于众数可由数据中出现次数最多的数写出；对于中位数，因为题中是按从小到大的顺序排列的，所以只要找出最中间的一个数（或最中间的两个数）即可，本题是最中间的一个数．‎ ‎【解答】解：一组数椐：3，4，5，6，6的平均数＝（3+4+5+6+6）÷5＝24÷5＝4.8．‎ ‎6出现的次数最多，故众数是6．‎ 按从小到大的顺序排列，最中间的一个数是5，故中位数为：5．‎ 故选：C．‎ ‎5．已知▱ABCD中，∠A+∠C＝80°，则∠B的度数为（　　）‎ A．80° B．100° C．120° D．140°‎ ‎【分析】根据平行四边形的对角相等、邻角互补的性质即可求解．‎ ‎【解答】解：∵四边形ABCD为平行四边形，‎ ‎∴∠A＝∠C，∠A+∠B＝180°‎ ‎∵∠A+∠C＝80°，‎ ‎∴∠A＝40°，‎ ‎∴∠B＝140°，‎ 故选：D．‎ ‎6．估算的值（　　）‎ A．在1和2之间 B．在2和3之间 C．在3和4之间 D．在4和5之间 ‎【分析】首先利用平方根的定义估算31前后的两个完全平方数25和36，从而判断的范围，再估算的范围即可．‎ ‎【解答】解：∵5＜＜6‎ ‎∴3＜＜4‎ 故选：C．‎ ‎7．若a，b，c满足，则关于x的方程ax2+bx+c＝0（a≠0）的解是（　　）‎ A．1，0 B．﹣1，‎0 ‎C．1，﹣1 D．无实数根 ‎【分析】分别把x＝1或x＝﹣1代入方程可得到足a+b+c＝0和a﹣b+c＝0，则根据一元二次方程的解的定义可判断方程的根．‎ ‎【解答】解：当x＝1时，a+b+c＝0，‎ 当x＝﹣1时，a﹣b+c＝0，‎ 所以关于x的方程ax2+bx+c＝0（a≠0）的解为1或﹣1．‎ 故选：C．‎ ‎8．从下列条件中选择一个条件添加后，还不能判定平行四边形ABCD是菱形，则这个条件是（　　）‎ A．AC⊥BD B．AC＝BD C．AB＝BC D．AD＝CD ‎【分析】根据菱形的判定方法即可一一判断．‎ ‎【解答】解：A、对角线垂直的平行四边形是菱形．不符合题意；‎ B、对角线相等的平行四边形是矩形．符合题意；‎ C、邻边相等的平行四边形是菱形．不符合题意；‎ D、邻边相等的平行四边形是菱形，不符合题意；‎ 故选：B．‎ ‎9．如图，已知双曲线y＝（k＜0）经过Rt△OAB斜边OA的中点D，且与直角边AB相交于点C，若点A的坐标为（﹣6，4），则△AOC的面积为（　　）‎ A．12 B．‎10 ‎C．9 D．8‎ ‎【分析】先根据线段的中点坐标公式得到D点坐标，再根据反比例函数图象上点的坐标特征得到k，根据反比例函数的比例系数k的几何意义得到S△OBC，然后利用△AOC的面积＝S△AOB﹣S△OBC进行计算．‎ ‎【解答】解：∵点A的坐标为（﹣6，4），点D为OA的中点，‎ ‎∴D点坐标为（﹣3，2），‎ ‎∴k＝﹣3×2＝6，即反比例函数解析式为y＝，‎ ‎∴S△OBC＝×6＝3，‎ ‎∴△AOC的面积＝S△AOB﹣S△OBC＝×4×6﹣3＝9．‎ 故选：C．‎ ‎10．小明使用图形计算器探究函数y＝的图象，他输入了一组a，b的值，得到了下面的函数图象，由学习函数的经验，可以推断出小明输入的a，b的值满足（　　）‎ A．a＞0，b＞0 B．a＞0，b＜‎0 ‎C．a＜0，b＞0 D．a＜0，b＜0‎ ‎【分析】由图象可知，当x＞0时，y＞0，可知a＞0；图象的右侧可以看作是反比例函数图象平移得到，由图可知向右平移，则b＞0；‎ ‎【解答】解：由图象可知，当x＞0时，y＞0，‎ ‎∴a＞0；‎ ‎∵图象的右侧可以看作是反比例函数图象平移得到，由图可知向右平移，‎ ‎∴b＞0；‎ 故选：A．‎ 二．填空题（共6小题）‎ ‎11．某组数据﹣2，﹣1，0，1，2的方差为　2　．‎ ‎【分析】先由平均数的计算公式先求出这组数据的平均数，再根据方差公式进行计算即可．‎ ‎【解答】解：这组数据的平均数是：（﹣2﹣1+0+1+2）÷5＝0，‎ 则数据的方差S2＝[（﹣2）2+（﹣1）2+12+22]＝2；‎ 故答案为：2．‎ ‎12．若+＝0，则x+y＝　10　．‎ ‎【分析】根据算术平方根的非负性得出x﹣8＝0，y﹣2＝0，求出x、y的值即可．‎ ‎【解答】解：根据题意，得x﹣8＝0，y﹣2＝0，‎ 所以x＝8，y＝2，‎ 所以x+y＝8+2＝10，‎ 故答案为：10．‎ ‎13．如图，▱ABCD的对角线相交于点O，且AD≠CD，过点O作OM⊥AC，交AD于点M．如果△CDM的周长为8，那么▱ABCD的周长是　16　．‎ ‎【分析】根据题意，OM垂直平分AC，所以MC＝MA，因此△CDM的周长＝AD+CD，可得平行四边形ABCD的周长．‎ ‎【解答】解：∵ABCD是平行四边形，‎ ‎∴OA＝OC，‎ ‎∵OM⊥AC，‎ ‎∴AM＝MC．‎ ‎∴△CDM的周长＝AD+CD＝8，‎ ‎∴平行四边形ABCD的周长是2×8＝16．‎ 故答案为16．‎ ‎14．已知x＝2是关于x的一元二次方程kx2+（k2﹣2）x+2k+4＝0的一个根，则k的值为　﹣3　．‎ ‎【分析】把x＝2代入kx2+（k2﹣2）x+2k+4＝0得4k+2k2﹣4+2k+4＝0，再解关于k的方程，然后根据一元二次方程的定义确定k的值．‎ ‎【解答】解：把x＝2代入kx2+（k2﹣2）x+2k+4＝0得4k+2k2﹣4+2k+4＝0，‎ 整理得k2+3k＝0，解得k1＝0，k2＝﹣3，‎ 因为k≠0，‎ 所以k的值为﹣3．‎ 故答案为﹣3．‎ ‎15．如图，正方形ABCD的边长为‎3cm，E为CD边上一点，∠DAE＝30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q．若PQ＝AE，则AP等于　2或‎1　cm．‎ ‎【分析】根据题意画出图形，过P作PN⊥BC，交BC于点N，由ABCD为正方形，得到AD＝DC＝PN，在直角三角形ADE中，利用锐角三角函数定义求出DE的长，进而利用勾股定理求出AE的长，根据M为AE中点求出AM的长，利用HL得到三角形ADE与三角形PQN全等，利用全等三角形对应边，对应角相等得到DE＝NQ，∠DAE＝∠NPQ＝30°，再由PN与DC平行，得到∠PFA＝∠DEA＝60°，进而得到PM垂直于AE，在直角三角形APM中，根据AM的长，利用锐角三角函数定义求出AP的长，再利用对称性确定出AP′的长即可．‎ ‎【解答】解：根据题意画出图形，过P作PN⊥BC，交BC于点N，‎ ‎∵四边形ABCD为正方形，‎ ‎∴AD＝DC＝PN，‎ 在Rt△ADE中，∠DAE＝30°，AD＝‎3cm，‎ ‎∴tan30°＝，即DE＝cm，‎ 根据勾股定理得：AE＝‎2cm，‎ ‎∵M为AE的中点，‎ ‎∴AM＝AE＝cm，‎ 在Rt△ADE和Rt△PNQ中，，‎ ‎∴Rt△ADE≌Rt△PNQ（HL），‎ ‎∴DE＝NQ，∠DAE＝∠NPQ＝30°，‎ ‎∵PN∥DC，‎ ‎∴∠PFA＝∠DEA＝60°，‎ ‎∴∠PMF＝90°，即PM⊥AF，‎ 在Rt△AMP中，∠MAP＝30°，cos30°＝，‎ ‎∴AP＝＝＝‎2cm；‎ 由对称性得到AP′＝DP＝AD﹣AP＝3﹣2＝‎1cm，‎ 综上，AP等于‎1cm或‎2cm．‎ 故答案为：1或2．‎ ‎16．如图，曲线l是由函数y＝在第一象限内的图象绕坐标原点O逆时针旋转45°得到的，过点A（﹣4，4），B（2，2）的直线与曲线l相交于点M、N，则△OMN的面积为　8　．‎ ‎【分析】由题意A（﹣4，4），B（2，2），可知OA⊥OB，建立如图新的坐标系（OB为x′轴，OA为y′轴，利用方程组求出M、N的坐标，根据S△OMN＝S△OBM﹣S△OBN计算即可．‎ ‎【解答】解：∵A（﹣4，4），B（2，2），‎ ‎∴OA⊥OB，‎ 建立如图新的坐标系，OB为x′轴，OA为y′轴．‎ 在新的坐标系中，A（0，8），B（4，0），‎ ‎∴直线AB解析式为y′＝﹣2x′+8，‎ 由，解得或，‎ ‎∴M（1，6），N（3，2），‎ ‎∴S△OMN＝S△OBM﹣S△OBN＝•4•6﹣•4•2＝8，‎ 故答案为8．‎ 三．解答题（共8小题）‎ ‎17．计算：‎ ‎（1）4﹣+；‎ ‎（2）（3﹣）．‎ ‎【分析】（1）先把二次根式化为最简二次根式，然后合并即可；‎ ‎（2）根据二次根式的乘法法则运算．‎ ‎【解答】解：（1）原式＝4﹣2+3‎ ‎＝2+3；‎ ‎（2）原式＝3﹣‎ ‎＝6﹣5‎ ‎＝1．‎ ‎18．选择合适的方法解一元二次方程：‎ ‎（1）4（x﹣5）2＝16；‎ ‎（2）（x+3）（x﹣1）＝5．‎ ‎【分析】（1）利用直接开平方法求解可得；‎ ‎（2）先整理为一般式，再利用因式分解法求解可得．‎ ‎【解答】解：（1）∵4（x﹣5）2＝16，‎ ‎∴（x﹣5）2＝4，‎ ‎∴x﹣5＝2或x﹣5＝﹣2，‎ 解得x1＝7，x2＝3；‎ ‎（2）将方程整理为一般式，得：x2+2x﹣8＝0，‎ ‎∴（x+4）（x﹣2）＝0，‎ 则x+4＝0或x﹣2＝0，‎ 解得x1＝﹣4，x2＝2．‎ ‎19．如图，在▱ABCD中，∠ABD＝90°，延长AB至点E，使BE＝AB，连接CE．求证：四边形BECD是矩形．‎ ‎【分析】由平行四边形的性质得出CD＝AB，CD∥AB，证出BE＝CD，则四边形BECD是平行四边形，证∠DBE＝90°，即可得出结论．‎ ‎【解答】证明：∵四边形ABD是平行四边形，‎ ‎∴CD＝AB，CD∥AB，‎ ‎∵BE＝AB，‎ ‎∴BE＝CD，‎ ‎∴四边形BECD是平行四边形，‎ ‎∵∠ABD＝90°，‎ ‎∴∠DBE＝90°，‎ ‎∴四边形BECD是矩形．‎ ‎20．已知图中的曲线是反比例函数y＝（m为常数）图象的一支．‎ ‎（1）根据图象位置，求m的取值范围；‎ ‎（2）若该函数的图象任取一点A，过A点作x轴的垂线，垂足为B，当△OAB的面积为4时，求m的值．‎ ‎【分析】（1）由反比例函数图象位于第一象限得到m﹣5大于0，即可求出m的范围；‎ ‎（2）根据反比例函数系数k的几何意义得出（m﹣5）＝4，解得即可．‎ ‎【解答】解：（1）∵这个反比例函数的图象分布在第一、第三象限，‎ ‎∴m﹣5＞0，‎ 解得m＞5．‎ ‎（2）∵S△OAB＝|k|，△OAB的面积为4，‎ ‎∴（m﹣5）＝4，‎ ‎∴m＝3．‎ ‎21．某商场经理对某一品牌旅游鞋近一个月的销售情况进行统计后，绘制了如下统计表与条形图：‎ 尺码（码）‎ 数量（双）‎ 百分比（%）‎ ‎36‎ ‎60‎ ‎30‎ ‎37‎ ‎30‎ ‎15‎ ‎38‎ a b ‎39‎ ‎40‎ ‎20‎ ‎40‎ c ‎5‎ ‎41‎ ‎10‎ ‎5‎ ‎（1）写出表中a，b，c的值；‎ ‎（2）补全条形图；‎ ‎（3）商场经理准备购进同一品牌的旅游鞋1500双，请根据市场实际情况估计他应该购进‎38码的鞋多少双？‎ ‎【分析】（1）根据‎36码鞋的双数除以占的百分比求出总双数，进而求出c的值，得出a的值，即可求出b的值；‎ ‎（2）补全条形统计图，如图所示；‎ ‎（3）根据（1）中的结果得出‎38码鞋占的百分比，乘以1500即可得到结果．‎ ‎【解答】解：（1）根据题意得：60÷30%＝200，c＝200×5%＝10，a＝200﹣60﹣30﹣40﹣10﹣10＝50；×100%＝25%，即b＝25；‎ ‎（2）补全条形统计图，如图所示：‎ ‎（3）由（1）可得‎38码的旅游鞋大约占25%，故购进1500双旅游鞋中应购进‎38码鞋375双．‎ ‎22．已知关于x的方程mx2+（‎3m+1）x+3＝0．‎ ‎（1）求证：不论m为任何实数，此方程总有实数根；‎ ‎（2）若方程mx2+（‎3m+1）x+3＝0有两个不同的整数根，且m为正整数，求m的值．‎ ‎【分析】（1）分类讨论：当m＝0时，方程变形一元一次方程，有一个实数解；当m≠0时，方程为一元二次方程，再进行判别式得到△＝（‎3m﹣1）2，易得△≥0，故判别式的意义得到方程有两个实数根，然后综合两种情况得到不论m为任何实数，此方程总有实数根；‎ ‎（2）先利用求根公式得到x1＝﹣3，x2＝﹣，再利用方程有两个不同的整数根，且m 为正整数和整数的整除性易得m＝1．‎ ‎【解答】（1）证明：当m＝0时，方程变形为x+3＝0，解得x＝﹣3；‎ 当m≠0时，△＝（‎3m+1）2﹣‎4m•3＝‎9m2‎﹣‎6m+1＝（‎3m﹣1）2，‎ ‎∵（‎3m﹣1）2，≥0，即△≥0，‎ ‎∴此时方程有两个实数根，‎ 所以不论m为任何实数，此方程总有实数根；‎ ‎（2）解：根据题意得m≠0且△＝（‎3m+1）2﹣‎4m•3＝（‎3m﹣1）2＞0，‎ x＝，‎ 所以x1＝﹣3，x2＝﹣，‎ ‎∵方程有两个不同的整数根，且m为正整数，‎ ‎∴m＝1．‎ ‎23．如图，在△ABC中，∠ACB＝90°，∠CAB＝30°，以线段AB为边向外作等边△ABD，点E是线段AB的中点，连接CE并延长交线段AD于点F．‎ ‎（1）求证：四边形BCFD为平行四边形；‎ ‎（2）若AB＝6，求平行四边形BCFD的面积．‎ ‎【分析】（1）在Rt△ABC中，E为AB的中点，则CE＝AB，BE＝AB，得到∠BCE＝∠EBC＝60°．由△AEF≌△BEC，得∠AFE＝∠BCE＝60°．又∠D＝60°，得∠AFE＝∠D＝60度．所以FC∥BD，又因为∠BAD＝∠ABC＝60°，所以AD∥BC，即FD∥BC，则四边形BCFD是平行四边形．‎ ‎（2）在Rt△ABC中，求出BC，AC即可解决问题；‎ ‎【解答】（1）证明：在△ABC中，∠ACB＝90°，∠CAB＝30°，‎ ‎∴∠ABC＝60°．‎ 在等边△ABD中，∠BAD＝60°，‎ ‎∴∠BAD＝∠ABC＝60°．‎ ‎∵E为AB的中点，‎ ‎∴AE＝BE．‎ 又∵∠AEF＝∠BEC，‎ ‎∴△AEF≌△BEC．‎ 在△ABC中，∠ACB＝90°，E为AB的中点，‎ ‎∴CE＝AB，BE＝AB．‎ ‎∴CE＝AE，‎ ‎∴∠EAC＝∠ECA＝30°，‎ ‎∴∠BCE＝∠EBC＝60°．‎ 又∵△AEF≌△BEC，‎ ‎∴∠AFE＝∠BCE＝60°．‎ 又∵∠D＝60°，‎ ‎∴∠AFE＝∠D＝60°．‎ ‎∴FC∥BD．‎ 又∵∠BAD＝∠ABC＝60°，‎ ‎∴AD∥BC，即FD∥BC．‎ ‎∴四边形BCFD是平行四边形．‎ ‎（2）解：在Rt△ABC中，∵∠BAC＝30°，AB＝6，‎ ‎∴BC＝AB＝3，AC＝BC＝3，‎ ‎∴S平行四边形BCFD＝3×＝9．‎ ‎24．已知点A、B分别是x轴、y轴上的动点，点C、D是某个函数图象上的点，当四边形ABCD（A、B、C、D 各点依次排列）为正方形时，称这个正方形为此函数图象的伴侣正方形．例如：如图，正方形ABCD是一次函数y＝x+1图象的其中一个伴侣正方形．‎ ‎（1）若某函数是一次函数y＝x+1，求它的图象的所有伴侣正方形的边长；‎ ‎（2）若某函数是反比例函数，它的图象的伴侣正方形为ABCD，点D（2，m）（m＜2）在反比例函数图象上，求m的值及反比例函数解析式．‎ ‎【分析】此题较为新颖，特别要注意审题和分析题意，耐心把题读完，知A、B为坐标轴上两点，C、D为函数图象上的两点．‎ ‎（1）先正确地画出图形，再利用正方形的性质确定相关点的坐标从而计算正方形的边长，注意思维的严密性；‎ ‎（2）因为ABCD为正方形，所以可作垂线得到全等三角形，利用点D（2，m）的坐标表示出点C的坐标从而求解．‎ ‎【解答】解：（1）如图1，当点A在x轴正半轴，点B在y轴负半轴上时，‎ ‎∵OC＝OD＝1，‎ ‎∴正方形ABCD的边长CD＝；‎ ‎∵当点A在x轴负半轴、点B在y轴正半轴上时，‎ ‎∴设正方形的边长为a，‎ ‎∴‎3a＝CD＝．‎ ‎∴a＝，‎ ‎∴正方形边长为 ，‎ ‎∴一次函数y＝x+1图象的伴侣正方形的边长为 或 ；‎ ‎（2）如图2，作DE，CF分别垂直于x、y轴，‎ ‎∵AB＝AD＝BC，∠DAE＝∠OBA＝∠FCB，‎ ‎∴△ADE≌△BAO≌△CBF．‎ ‎∵m＜2，‎ ‎∴DE＝OA＝BF＝m，OB＝CF＝AE＝2﹣m，‎ ‎∴OF＝BF+OB＝2，‎ ‎∴C点坐标为（2﹣m，2），‎ 设反比例函数的解析式为：，‎ ‎∵D（2，m），C（2﹣m，2）‎ ‎∴，‎ ‎∴由②得：k＝‎2m③，‎ ‎∴把k＝‎2m代入①得：‎2m＝2（2﹣m），‎ ‎∴解得m＝1，k＝2，‎ ‎∴反比例函数的解析式为y＝．‎