2019-2020学年陕西渭南七年级上数学期中试卷

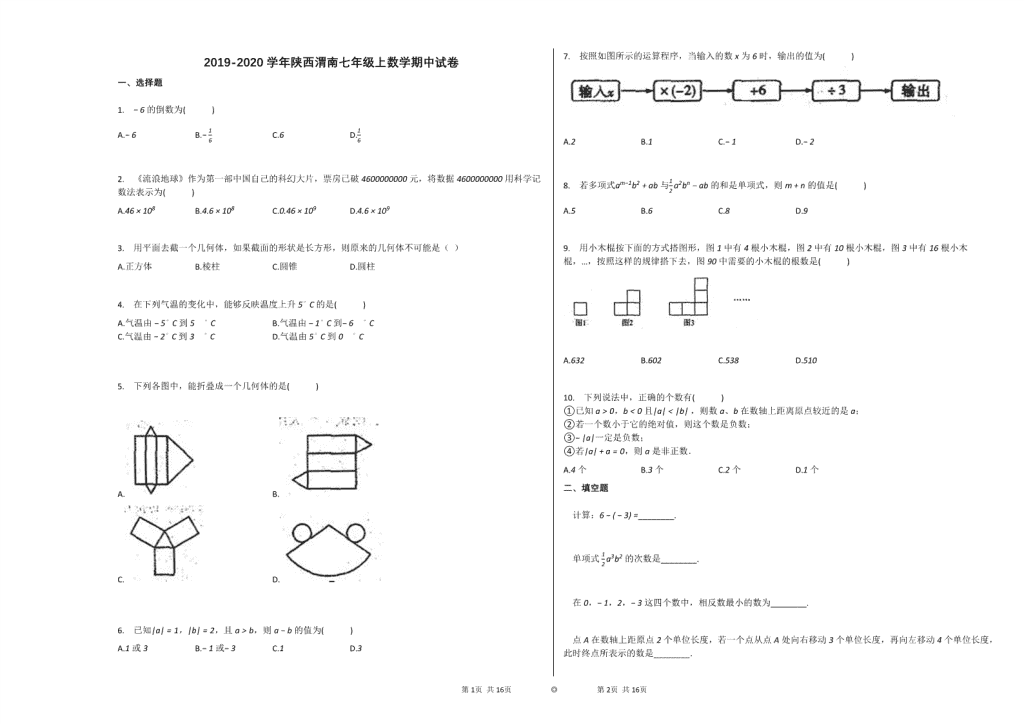
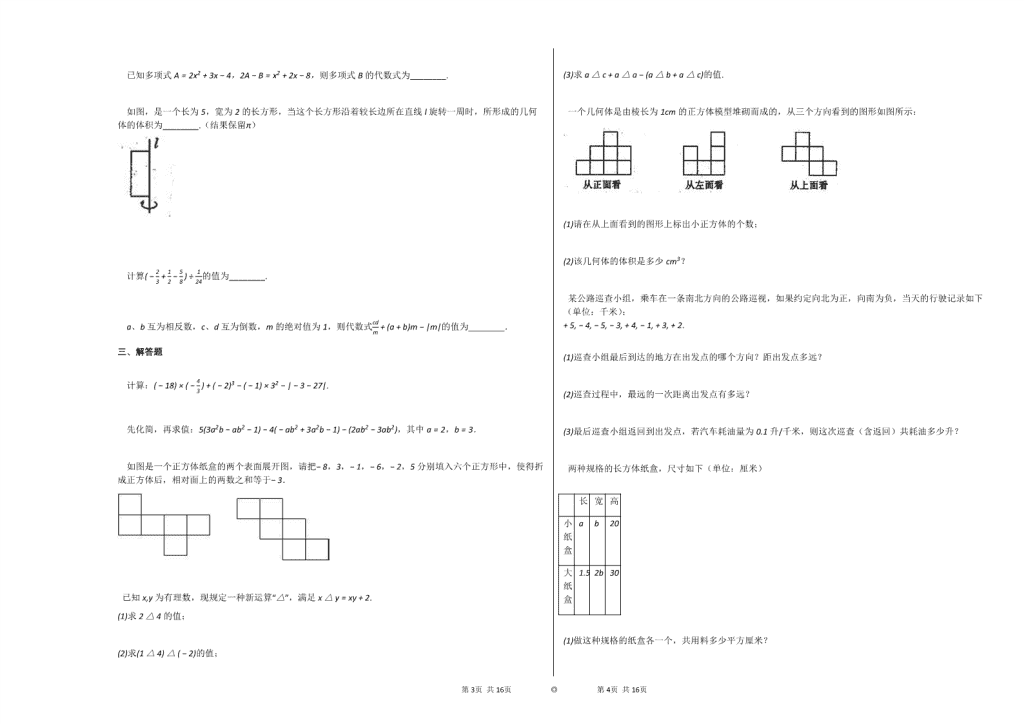
2019-2020学年陕西渭南七年级上数学期中试卷

‎2019-2020学年陕西渭南七年级上数学期中试卷 一、选择题 ‎ ‎ ‎1. ‎−6‎的倒数为(        ) ‎ A.‎−6‎ B.‎−‎‎1‎‎6‎ C.‎6‎ D.‎‎1‎‎6‎ ‎ ‎ ‎2. 《流浪地球》作为第一部中国自己的科幻大片，票房已破‎4600000000‎元，将数据‎4600000000‎用科学记数法表示为(        ) ‎ A.‎46×‎‎10‎‎8‎ B.‎4.6×‎‎10‎‎8‎ C.‎0.46×‎‎10‎‎9‎ D.‎‎4.6×‎‎10‎‎9‎ ‎ ‎ ‎3. 用平面去截一个几何体，如果截面的形状是长方形，则原来的几何体不可能是（ ） ‎ A.正方体 B.棱柱 C.圆锥 D.圆柱 ‎ ‎ ‎4. 在下列气温的变化中，能够反映温度上升 ‎5‎‎∘‎C 的是(        ) ‎ A.气温由 ‎−‎5‎‎∘‎C 到‎5‎​‎‎∘‎C B.气温由 ‎−‎1‎‎∘‎C 到‎−6‎​‎‎∘‎C C.气温由 ‎−‎2‎‎∘‎C 到‎3‎​‎‎∘‎C D.气温由 ‎5‎‎∘‎C 到‎0‎​‎‎∘‎C ‎ ‎ ‎ ‎5. 下列各图中，能折叠成一个几何体的是(        ) ‎ A. B. C. D. ‎ ‎ ‎ ‎6. 已知‎|a|=1，|b|=2‎，且a>b，则a−b的值为(        ) ‎ A.‎1‎或‎3‎ B.‎−1‎或‎−3‎ C.‎1‎ D.‎‎3‎ ‎ ‎ ‎7. 按照如图所示的运算程序，当输入的数x为‎6‎时，输出的值为(        ) ‎ A.‎2‎ B.‎1‎ C.‎−1‎ D.‎‎−2‎ ‎ ‎ ‎8. 若多项式am−1‎b‎2‎‎+ab与‎1‎‎2‎a‎2‎bn‎−ab的和是单项式，则m+n的值是(        ) ‎ A.‎5‎ B.‎6‎ C.‎8‎ D.‎‎9‎ ‎ ‎ ‎9. 用小木棍按下面的方式搭图形，图‎1‎中有‎4‎根小木棍，图‎2‎中有‎10‎根小木棍，图‎3‎中有‎16‎根小木棍，…，按照这样的规律搭下去，图‎90‎中需要的小木棍的根数是(        ) ‎ A.‎632‎ B.‎602‎ C.‎538‎ D.‎‎510‎ ‎ ‎ ‎10. 下列说法中，正确的个数有(        ) ①已知 a>0‎，b<0‎ 且‎|a|<|b|‎ ，则数a、b在数轴上距离原点较近的是 a； ②若一个数小于它的绝对值，则这个数是负数； ③‎−|a|‎一定是负数； ④若‎|a|+a=0‎，则a是非正数． ‎ A.‎4‎个 B.‎3‎个 C.‎2‎个 D.‎1‎个 二、填空题 ‎ ‎ ‎ 计算：‎6−(−3)=‎________. ‎ ‎ ‎ ‎ 单项式 ‎1‎‎2‎a‎3‎b‎2‎ 的次数是________. ‎ ‎ ‎ ‎ 在‎0‎，‎−1‎，‎2‎，‎−3‎这四个数中，相反数最小的数为________. ‎ ‎ ‎ ‎ 点A在数轴上距原点‎2‎个单位长度，若一个点从点A处向右移动‎3‎个单位长度，再向左移动‎4‎个单位长度，此时终点所表示的数是________． ‎ 第13页 共16页 ◎ 第14页 共16页 ‎ ‎ ‎ 已知多项式A=2x‎2‎+3x−4，2A−B=x‎2‎+2x−8，‎则多项式B的代数式为________. ‎ ‎ ‎ ‎ 如图，是一个长为‎5‎，宽为‎2‎的长方形，当这个长方形沿着较长边所在直线l旋转一周时，所形成的几何体的体积为________.（结果保留π） ‎ ‎ ‎ ‎ 计算‎(−‎2‎‎3‎+‎1‎‎2‎−‎5‎‎8‎)÷‎‎1‎‎24‎的值为________. ‎ ‎ ‎ ‎ a、b互为相反数，c、d互为倒数，m的绝对值为‎1‎，则代数式cdm‎+(a+b)m−|m|‎的值为________． ‎ 三、解答题 ‎ ‎ ‎ 计算：‎(−18)×(−‎4‎‎3‎)+(−2‎)‎‎3‎−(−1)×‎3‎‎2‎−|−3−27|‎. ‎ ‎ ‎ ‎ 先化简，再求值：‎5(3a‎2‎b−ab‎2‎−1)−4(−ab‎2‎+3a‎2‎b−1)−(2ab‎2‎−3ab‎2‎)‎，其中a=2‎，b=3‎． ‎ ‎ ‎ ‎ 如图是一个正方体纸盒的两个表面展开图，请把‎−8‎，‎3‎，‎−1‎，‎−6‎，‎−2‎，‎5‎分别填入六个正方形中，使得折成正方体后，相对面上的两数之和等于‎−3‎． ‎ ‎ ‎ ‎ 已知x,y为有理数，现规定一种新运算“‎△‎”，满足x△y=xy+2‎. ‎ ‎(1)‎求‎2△4‎的值；‎ ‎ ‎ ‎(2)‎求‎(1△4)△(−2)‎的值；‎ ‎ ‎ ‎(3)‎求a△c+a△a−(a△b+a△c)‎的值.‎ ‎ ‎ ‎ 一个几何体是由棱长为‎1cm的正方体模型堆砌而成的，从三个方向看到的图形如图所示： ‎ ‎(1)‎请在从上面看到的图形上标出小正方体的个数；‎ ‎ ‎ ‎(2)‎该几何体的体积是多少cm‎3‎？‎ ‎ ‎ ‎ 某公路巡查小组，乘车在一条南北方向的公路巡视，如果约定向北为正，向南为负，当天的行驶记录如下（单位：千米）： ‎+5,−4,−5,−3,+4,−1,+3,+2‎. ‎ ‎(1)‎巡查小组最后到达的地方在出发点的哪个方向？距出发点多远？‎ ‎ ‎ ‎(2)‎巡查过程中，最远的一次距离出发点有多远？‎ ‎ ‎ ‎(3)‎最后巡查小组返回到出发点，若汽车耗油量为‎0.1‎升/千米，则这次巡查（含返回）共耗油多少升？‎ ‎ ‎ ‎ 两种规格的长方体纸盒，尺寸如下（单位：厘米） ‎ ‎ ‎ 长 宽 高 小纸盒 a b ‎20‎ 大纸盒 ‎1.5a ‎2b ‎30‎ ‎ ‎ ‎(1)‎做这种规格的纸盒各一个，共用料多少平方厘米？‎ ‎ ‎ ‎(2)‎做一个大纸盒与做三个小纸盒，哪个用料多？多多少平方厘米？‎ ‎ ‎ ‎(3)‎若a=3‎，b=‎‎3‎‎2‎，且每平方厘米的费用为‎0.01‎元，则做一个大纸盒比做一个小纸盒多用多少元？‎ 第13页 共16页 ◎ 第14页 共16页 第13页 共16页 ◎ 第14页 共16页 参考答案与试题解析 ‎2019-2020学年陕西渭南七年级上数学期中试卷 一、选择题 ‎1.‎ ‎【答案】‎ B ‎【考点】‎ 倒数 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎−6×(−‎1‎‎6‎)=1‎， 所以‎−6‎的倒数为‎−‎‎1‎‎6‎. 故选B. ‎ ‎2.‎ ‎【答案】‎ D ‎【考点】‎ 科学记数法--表示较大的数 ‎【解析】‎ 科学记数法的表示形式为a×‎‎10‎n的形式，其中‎1≤|a|<10‎，n为整数．确定n的值是易错点，由于‎4 600 000 000‎有‎10‎位，所以可以确定n=10−1=9‎．‎ ‎【解答】‎ 解：‎4 600 000 000=4.6×‎‎10‎‎9‎． 故选D．‎ ‎3.‎ ‎【答案】‎ C ‎【考点】‎ 截一个几何体 ‎【解析】‎ 根据正方体、棱柱、圆锥、圆柱的特点判断即可．‎ ‎【解答】‎ 解：A、正方体的截面可以是长方形，不符合题意； B、棱柱的截面可以是长方形，不符合题意； C、圆锥由一个平面和一个曲面，截面最多有三条边，截面不可能是长方形，符合题意； D、用垂直于地面的一个平面截圆柱截面为矩形，不符合题意． 故选C.‎ ‎4.‎ ‎【答案】‎ C ‎【考点】‎ 有理数的混合运算 正数和负数的识别 ‎【解析】‎ 根据该地区高度每增加‎1‎千米，气温就下降大约‎5‎​‎‎∘‎C，求出‎4‎千米中有几个‎1‎千米，温度就下降几个‎5‎​‎‎∘‎C，进而求出下降的温度，然后用地面温度减去下降的温度列出算式，即可求出‎4‎千米高空的气温．‎ ‎【解答】‎ 解：A，‎5−(−5)=10‎，不符合题意； B，‎−6−(−1)=−5‎，不符合题意； C，‎3−(−2)=5‎，符合题意； D，‎0−5=−5‎，不符合题意. 故选C.‎ ‎5.‎ ‎【答案】‎ B ‎【考点】‎ 展开图折叠成几何体 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：观察‎4‎个图，只有B选项中的图可以折叠成一个几何体，折叠成三棱柱. 故选B.‎ ‎6.‎ ‎【答案】‎ A ‎【考点】‎ 绝对值 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：∵ ‎|a|=1，|b|=2‎， ∴ a=±1，b=±2‎， ∵ a>b， ∴ a=±1，b=−2‎， 当a=1，b=−2‎时，a−b=1−(−2)=3‎； 当a=−1，b=−2‎时，a−b=−1−(−2)=1‎. 故选A.‎ ‎7.‎ ‎【答案】‎ D ‎【考点】‎ 有理数的混合运算 ‎【解析】‎ 此题暂无解析 第13页 共16页 ◎ 第14页 共16页 ‎【解答】‎ 解：由题知：‎[6×(−2)+6]÷3=−2‎. 故选D．‎ ‎8.‎ ‎【答案】‎ A ‎【考点】‎ 合并同类项 单项式 ‎【解析】‎ 本题考查了合并同类项的知识．‎ ‎【解答】‎ 解：∵ 多项式am−1‎b‎2‎‎+ab与‎1‎‎2‎a‎2‎bn‎−ab的和是单项式， ∴ 单项式am−1‎b‎2‎与‎1‎‎2‎a‎2‎bn是同类项， ∴ m−1=2‎，n=2‎， ∴ m=3‎，n=2‎， ∴ m+n=5‎． 故选A．‎ ‎9.‎ ‎【答案】‎ C ‎【考点】‎ 规律型：图形的变化类 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：第‎1‎个图形用了‎4‎根火柴， 第‎2‎个图形用了‎4+6=10‎根火柴， 第‎3‎个图形用了‎4+6+6=16‎根火柴， 第‎4‎个图形用了‎4+6+6+6=22‎根火柴， … 第n个图形用了‎4+6(n−1)‎根火柴． 所以图‎90‎中需要的小木棍的根数是‎4+6×89=538‎. 故选C．‎ ‎10.‎ ‎【答案】‎ B ‎【考点】‎ 绝对值 相反数 数轴 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：本题可通过特殊值法、绝对值及相反数的意义，逐一判断得到正确结论． 在数轴上，绝对值小的数距离原点较近，故①正确； 正数和‎0‎的绝对值等于它本身，负数小于它的绝对值，故②正确； ‎−|0|=0‎，不是负数，故③不正确； 当a是非正数时，‎|a|+a=0‎，故④正确． 综上正确的是①②④． 故选B．‎ 二、填空题 ‎【答案】‎ ‎9‎ ‎【考点】‎ 有理数的加减混合运算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎6−(−3)=6+3=9‎. 故答案为：‎9‎.‎ ‎【答案】‎ ‎5‎ ‎【考点】‎ 单项式的系数与次数 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：单项式的次数为：‎3+2=5‎. 故答案为：‎5‎. ‎ ‎【答案】‎ ‎2‎ ‎【考点】‎ 相反数 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎0‎的相反数是‎0‎； ‎−1‎的相反数是‎1‎； ‎2‎的相反数是‎−2‎； ‎−3‎的相反数是‎3‎； ∵ ‎−2<0<1<3‎， ∴ 在‎0，−1，2，−3‎中，相反数最小的数是‎2‎. 故答案为：‎2‎.‎ ‎【答案】‎ ‎−3‎或‎1‎ ‎【考点】‎ 第13页 共16页 ◎ 第14页 共16页 数轴 ‎【解析】‎ 根据题意得出A点表示的数进而利用平移规律得出答案．‎ ‎【解答】‎ 解：∵ 点A在数轴上距原点‎2‎个单位长度，， ∴ 点A表示的数为‎−2‎或‎2‎， 当点A表示‎−2‎时，终点所表示的数是‎−2+3−4=−3‎； 当点A表示‎2‎时，终点所表示的数是‎2+3−4=1‎. 故答案为：‎−3‎或‎1‎．‎ ‎【答案】‎ ‎3x‎2‎+4x ‎【考点】‎ 多项式的概念的应用 单项式乘多项式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：因为A=2x‎2‎+3x−4，2A−B=x‎2‎+2x−8，‎ 所以B=2A−(x‎2‎+2x−8)=4x‎2‎+6x−8−x‎2‎−2x+8=3x‎2‎+4x 故所求的多项式为：‎3x‎2‎+4x. 故答案为：‎3x‎2‎+4x.‎ ‎【答案】‎ ‎20π ‎【考点】‎ 点、线、面、体 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：绕直线旋转一周得到圆柱体积为：π×‎2‎‎2‎×5=20π. 故答案为：‎20π.‎ ‎【答案】‎ ‎−19‎ ‎【考点】‎ 有理数的混合运算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(−‎2‎‎3‎+‎1‎‎2‎−‎5‎‎8‎)÷‎‎1‎‎24‎ ‎=(−‎16‎‎24‎+‎12‎‎24‎−‎15‎‎24‎)÷‎‎1‎‎24‎ ‎=−‎19‎‎24‎×24‎ ‎=−19‎ 故答案为：‎−19‎. ‎ ‎【答案】‎ ‎0‎或‎−2‎ ‎【考点】‎ 列代数式求值方法的优势 倒数 绝对值 相反数 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：∵ a、b互为相反数， ∴ a+b=0‎， ∵ c、d互为倒数， ∴ cd=1‎， ∵ m的绝对值为‎1‎， ∴ m=±1‎. 当m=1‎时，cdm‎+(a+b)m−|m|=1−1=0‎； 当m=−1‎时，cdm‎+(a+b)m−|m|=−1−1=−2‎. 综上所述，代数式的值为‎0‎或‎−2‎． 故答案为：‎0‎或‎−2‎．‎ 三、解答题 ‎【答案】‎ 解：原式‎=24+(−8)−(−1)×9−|−30|‎ ‎=24−8+9−30‎ ‎=−5‎.‎ ‎【考点】‎ 有理数的混合运算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：原式‎=24+(−8)−(−1)×9−|−30|‎ ‎=24−8+9−30‎ ‎=−5‎.‎ ‎【答案】‎ 解：原式‎=15a‎2‎b−5ab‎2‎−5+4ab‎2‎−12a‎2‎b+4−2ab‎2‎+3ab‎2‎ ‎=(15a‎2‎b−12a‎2‎b)+(−5ab‎2‎+4ab‎2‎−2ab‎2‎+3ab‎2‎)+(4−5)‎ ‎=3a‎2‎b−1‎， 当a=2‎，b=3‎时，原式‎=3×4×3−1=35‎．‎ ‎【考点】‎ 整式的加减--化简求值 ‎【解析】‎ 原式去括号合并得到最简结果，把a与b的值代入计算即可求出值．‎ ‎【解答】‎ 第13页 共16页 ◎ 第14页 共16页 解：原式‎=15a‎2‎b−5ab‎2‎−5+4ab‎2‎−12a‎2‎b+4−2ab‎2‎+3ab‎2‎ ‎=(15a‎2‎b−12a‎2‎b)+(−5ab‎2‎+4ab‎2‎−2ab‎2‎+3ab‎2‎)+(4−5)‎ ‎=3a‎2‎b−1‎， 当a=2‎，b=3‎时，原式‎=3×4×3−1=35‎．‎ ‎【答案】‎ 解：如图所示（答案不唯一）． ‎ ‎【考点】‎ 正方体相对两个面上的文字 ‎【解析】‎ 由平面图形的折叠及立体图形的表面展开图的特点解题．‎ ‎【解答】‎ 解：如图所示（答案不唯一）． ‎ ‎【答案】‎ 解：‎(1)‎∵ x△y=xy+2‎， ∴ ‎2△4=2×4+2=8+2=10‎.‎ ‎(2)‎‎(1△4)△(−2)‎‎ ‎=(1×4+2)△(−2)‎ ‎=6△(−2)‎ ‎=6×(−2)+2‎ ‎=(−12)+2‎ ‎=−10‎.‎ ‎(3)‎a△c+a△a=ac+2+a‎2‎+2=ac+a‎2‎+4‎‎，  a△b+a△c=ab+2+ac+2=ab+ac+4‎，  ∴ a△c+a△a−(a△b+a△c)‎‎=ac+a‎2‎+4−(ab+ac+4)=a‎2‎−ab.‎ ‎【考点】‎ 定义新符号 有理数的混合运算 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎∵ x△y=xy+2‎， ∴ ‎2△4=2×4+2=8+2=10‎.‎ ‎(2)‎‎(1△4)△(−2)‎‎ ‎=(1×4+2)△(−2)‎ ‎=6△(−2)‎ ‎=6×(−2)+2‎ ‎=(−12)+2‎ ‎=−10‎.‎ ‎(3)‎a△c+a△a=ac+2+a‎2‎+2=ac+a‎2‎+4‎‎，  a△b+a△c=ab+2+ac+2=ab+ac+4‎，  ∴ a△c+a△a−(a△b+a△c)‎‎=ac+a‎2‎+4−(ab+ac+4)=a‎2‎−ab.‎ ‎【答案】‎ 解：‎(1)‎由题知： ‎ ‎(2)‎由‎(1)‎可知，组成这个几何体所需的小正方体的个数为‎10‎个； 故体积为：‎1×1×1×10=10(cm‎3‎)‎. 答：该几何体的体积是‎10cm‎3‎.‎ ‎【考点】‎ 由三视图确定几何体的体积或面积 简单几何体的三视图 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎由题知： ‎ ‎(2)‎由‎(1)‎可知，组成这个几何体所需的小正方体的个数为‎10‎个； 故体积为：‎1×1×1×10=10(cm‎3‎)‎. 答：该几何体的体积是‎10cm‎3‎.‎ ‎【答案】‎ 第13页 共16页 ◎ 第14页 共16页 解：‎(1)5+(−4)+(−5)+(−3)+4+(−1)+3+2=1‎（千米）， 则巡查小组最后到达的地方在出发点的北方，距出发点‎1‎千米. ‎ ‎(2)‎第一次距离出发点‎5‎千米; 第二次：‎5+(−4)=1‎，距离出发点‎1‎千米 第三次：‎1+(−5)=−4‎，距离出发点‎4‎千米； 第四次：‎−4+(−3)=−7‎，距离出发点‎7‎千米； 第五次：‎−7+4=−3‎，距离出发点‎3‎千米； 第六次：‎−3−1=−4‎，距离出发点‎4‎千米； 第七次：‎−4+3=−1‎，距离出发点‎1‎千米； 第八次：‎−1+2=1‎，距离出发点‎1‎千米. 答：最远的一次距离出发点‎7‎千米.‎ ‎(3)‎由于最后巡查小组回到出发点，所以整个巡查过程的路程还需加上最后一次返回A点时的路程， ‎(5+|−4|+|−5|+|−3|+4+|−1|+3+2+1)×0.1‎ ‎=28×0.1‎ ‎=2.8‎（升）. 答：这次巡查（含返回）共耗油‎2.8‎升.‎ ‎【考点】‎ 有理数的加减混合运算 绝对值 正数和负数的识别 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)5+(−4)+(−5)+(−3)+4+(−1)+3+2=1‎（千米）， 则巡查小组最后到达的地方在出发点的北方，距出发点‎1‎千米. ‎ ‎(2)‎第一次距离出发点‎5‎千米; 第二次：‎5+(−4)=1‎，距离出发点‎1‎千米 第三次：‎1+(−5)=−4‎，距离出发点‎4‎千米； 第四次：‎−4+(−3)=−7‎，距离出发点‎7‎千米； 第五次：‎−7+4=−3‎，距离出发点‎3‎千米； 第六次：‎−3−1=−4‎，距离出发点‎4‎千米； 第七次：‎−4+3=−1‎，距离出发点‎1‎千米； 第八次：‎−1+2=1‎，距离出发点‎1‎千米. 答：最远的一次距离出发点‎7‎千米.‎ ‎(3)‎由于最后巡查小组回到出发点，所以整个巡查过程的路程还需加上最后一次返回A点时的路程， ‎(5+|−4|+|−5|+|−3|+4+|−1|+3+2+1)×0.1‎ ‎=28×0.1‎ ‎=2.8‎（升）. 答：这次巡查（含返回）共耗油‎2.8‎升.‎ ‎【答案】‎ 解：‎(1)‎‎2(1.5a×2b+1.5a×30+2b×30)+2(ab+20a+20b)‎ ‎=6ab+90a+120b+2ab+40a+40b ‎=8ab+130a+160b（平方厘米）． 答：共用料‎(8ab+130a+160b)‎平方厘米.‎ ‎(2)‎‎2(1.5a×2b+1.5a×30+2b×30)=6ab+90a+120b‎（平方厘米）； ‎2(ab+20a+20b)×3=6ab+120a+120b（平方厘米）； ‎(6ab+120a+120b)−(6ab+90a+120b)=30a（平方厘米）． 答：做三个小纸盒的用料多，多‎30a平方厘米．‎ ‎(3)‎一个大纸盒比一个小纸盒多用的料：‎ ‎6ab+90a+120b−(2ab+40a+40b)=4ab+50a+80b‎(平方厘米).‎ 当a=3‎，b=‎‎3‎‎2‎，且每平方厘米的费用为‎0.01‎时，则可得：‎ ‎0.01×(4ab+50a+80b)‎ ‎=0.01×(4×3×‎3‎‎2‎+50×3+80×‎3‎‎2‎)‎ ‎=2.88‎‎(元).‎ 答：做一个大纸盒比做一个小纸盒多用‎2.88‎元.‎ ‎【考点】‎ 整式的混合运算 整式的加减 列代数式 ‎【解析】‎ 此题暂无解析 ‎【解答】‎ 解：‎(1)‎‎2(1.5a×2b+1.5a×30+2b×30)+2(ab+20a+20b)‎ ‎=6ab+90a+120b+2ab+40a+40b ‎=8ab+130a+160b（平方厘米）． 答：共用料‎(8ab+130a+160b)‎平方厘米.‎ ‎(2)‎‎2(1.5a×2b+1.5a×30+2b×30)=6ab+90a+120b‎（平方厘米）； ‎2(ab+20a+20b)×3=6ab+120a+120b（平方厘米）； ‎(6ab+120a+120b)−(6ab+90a+120b)=30a（平方厘米）． 答：做三个小纸盒的用料多，多‎30a平方厘米．‎ ‎(3)‎一个大纸盒比一个小纸盒多用的料：‎ ‎6ab+90a+120b−(2ab+40a+40b)=4ab+50a+80b‎(平方厘米).‎ 当a=3‎，b=‎‎3‎‎2‎，且每平方厘米的费用为‎0.01‎时，则可得：‎ ‎0.01×(4ab+50a+80b)‎ ‎=0.01×(4×3×‎3‎‎2‎+50×3+80×‎3‎‎2‎)‎ ‎=2.88‎‎(元).‎ 答：做一个大纸盒比做一个小纸盒多用‎2.88‎元.‎ 第13页 共16页 ◎ 第14页 共16页