- 2021-10-26 发布 |
- 37.5 KB |
- 7页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020学年七年级数学上册 一次函数之存在性问题(二)讲义 (新版)鲁教版
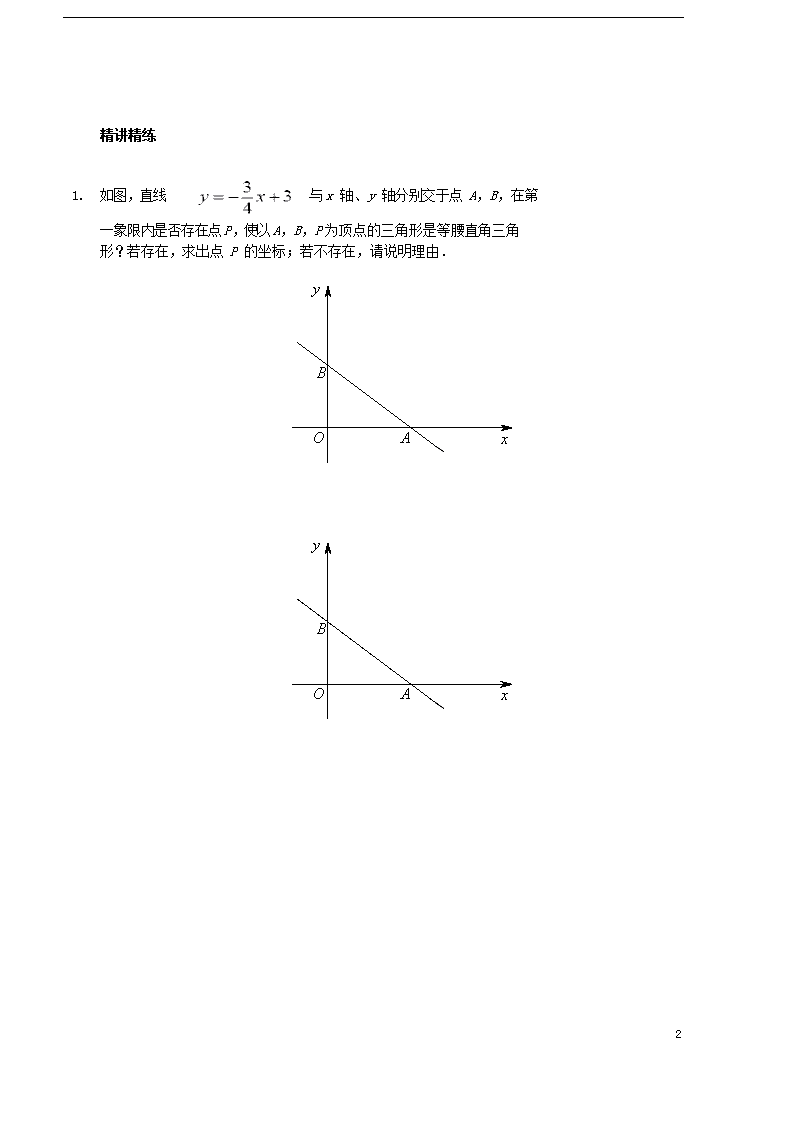
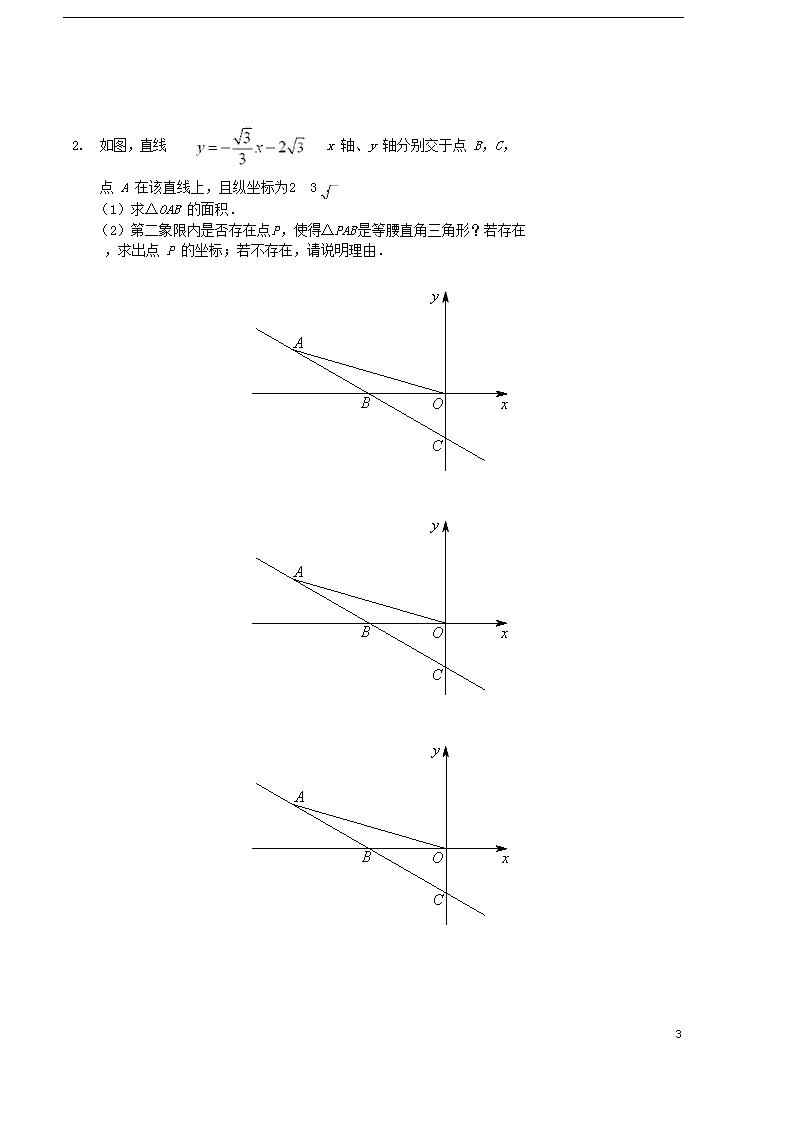
1 一次函数之存在性问题(二)(讲义) 课前预习 1 已知线段 AB,在平面内是否存在点 C,使得△ABC 为等腰直角三角形? 若存在,请作图找出所有满足条件的点 C;若不存在,请说明理由.( 保留作图痕迹) A B 2 用铅笔做讲义第 1,2 题,并将计算、演草保留在讲义上,先看知识点睛 ,再做题,思路受阻时(某个点做了 2~3 分钟) 重复上述动作,若仍 无法解决,课堂重点听. 知识点睛 1. 一次函数背景下解决存在性问题的思考方向: ①研究背景图形,把函数信息( )转化为 几何信息; ②分析不变特征,确定分类标准; ③分析特殊状态的形成因素,画出符合题意的图形并求解. 2. 不变特征举例: ①等腰直角三角形 根据直角顶点确定分类标准,然后借助两腰相等或者45°角确定点的位 置. ②含特殊角的直角三角形 根据直角顶点确定分类标准,然后根据特殊角再次分类,进而作图确定 点的位置. 2 精讲精练 1. 如图,直线 与 x 轴、y 轴分别交于点 A,B,在第 一象限内是否存在点 P,使以 A,B,P 为顶点的三角形是等腰直角三角 形?若存在,求出点 P 的坐标;若不存在,请说明理由. y B O A x y B O A x 3 2. 如图,直线 x 轴、y 轴分别交于点 B,C, 点 A 在该直线上,且纵坐标为2 3 . (1)求△OAB 的面积. (2)第二象限内是否存在点 P,使得△PAB 是等腰直角三角形?若存在 ,求出点 P 的坐标;若不存在,请说明理由. y A B O x C y A B O x C y A B O x C 4 y Q P O A x y O A x y O A x 3 如图,在平面直角坐标系中,点 A 的坐标为(2,0),Q 是直线 x=3 上的一个动点,y 轴正半轴上是否存在点 P,使△APQ 为等腰直角 三角形?若存在,求出点 P 的坐标;若不存在,请说明理由. x=3 x=3 x=3 5 4.如图,直线 与X 轴、Y轴分别交于点A、B.第 一象限内是否存在点 P,使以 P,O,B 为顶点的三角形是含 60°角的直角三角形?若存在,求出点 P 的坐标;若不存在, 请说明 理由. y B O A x y B O A x 6 4 如图,直线 y 3x 3 与 x 轴、y 轴分别交于点 A,B.第一 象限内是否存在点 P,使以 P,O,B 为顶点的三角形是含 30° 角的直角三 角形?若存在,求出点 P 的坐标;若不存在,请说明理由. y B A O x y B A O x y B A O x 7查看更多