- 2021-10-25 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
苏教版数学七年级上册教案《2-6 有理数的乘法与除法》第3课时
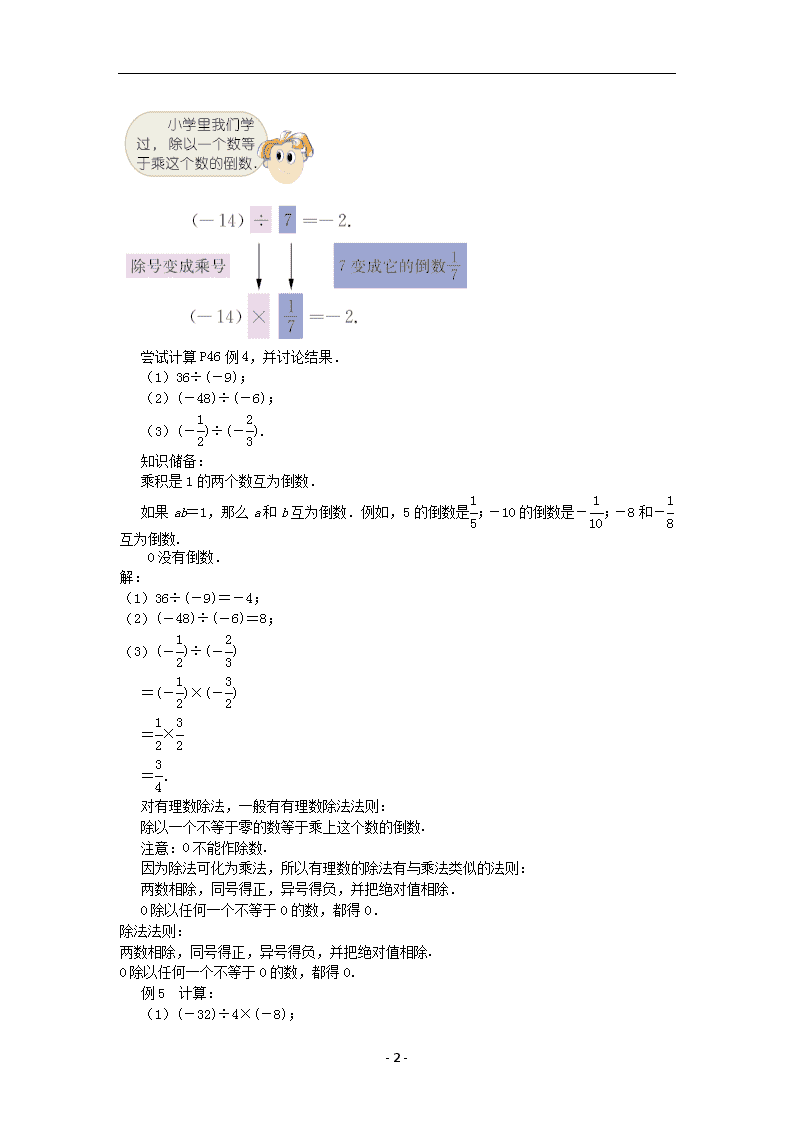
- 1 - 2.6 有理数的乘法与除法 第 3 课时 教学目标 1.知道除法是乘法的逆运算; 2.理解有理数除法的法则,会进行有理数的除法运算; 3.会求有理数的倒数. 教学重难点 【教学重点】 1.理解有理数除法的法则; 2.会进行有理数的除法运算. 【教学难点】 会进行有理数的除法运算. 课前准备 课件. 教学过程 一、创设情境 某地某周每天上午 8 时的气温记录如下: 这周每天上午 8 时的平均气温为: [(-3)+(-3)+(-2)+(-3)+0+(-2)+(-1)]÷7, 即(-14)÷7, 如何计算(-14)÷7? 引导学生尝试练习,并探索规律. 二、新知讲解: 分组合作讨论并交流 P45 议一议,试一试. 如何计算(-14)÷7? (-14)÷7=(-14)× 1 7 - 2 - 尝试计算 P46 例 4,并讨论结果. (1)36÷(-9); (2)(-48)÷(-6); (3)(- 1 2 )÷(- 2 3 ). 知识储备: 乘积是 1 的两个数互为倒数. 如果 ab=1,那么 a 和 b 互为倒数.例如,5 的倒数是 1 5 ;-10 的倒数是- 1 10 ;-8 和 - 1 8 互为倒数. 0 没有倒数. 解: (1)36÷(-9)=-4; (2)(-48)÷(-6)=8; (3)(- 1 2 )÷(- 2 3 ) =(- 1 2 )×(- 3 2 ) = 1 2 × 3 2 = 3 4 . 对有理数除法,一般有有理数除法法则: 除以一个不等于零的数等于乘上这个数的倒数. 注意:0不能作除数. 因为除法可化为乘法,所以有理数的除法有与乘法类似的法则: 两数相除,同号得正,异号得负,并把绝对值相除. 0 除以任何一个不等于 0 的数,都得 0. 除法法则: 两数相除,同号得正,异号得负,并把绝对值相除. 0 除以任何一个不等于 0的数,都得 0. 例 5 计算: - 3 - (1)(-32)÷4×(-8); (2)17×(-6)÷(-5); (3)(-81)÷ 9 4 × 4 9 ÷(-16). 解: (1)(-32)÷4×(-8) =(-32)× 1 4 ×(-8) =(-8)×(-8) =64; (2)17×(-6)÷(-5) =17×(-6)×(- 1 5 ) =(-102)×(- 1 5 ) = 102 5 ; (3)(-81)÷ 9 4 × 4 9 ÷(-16) =(-81)× 4 9 × 4 9 ÷(-16) =-36× 4 9 ×(- 1 16 ) =-16×(- 1 16 ) =1. 尝试计算例 6,并讨论结果. 例 6 计算( 1 3 - 1 2 )÷1 1 4 ÷ 1 10 . 解 ( 1 3 - 1 2 )÷1 1 4 ÷ 1 10 =(- 1 6 )× 4 5 ×10 =- 4 3 . 让学生分小组交流,然后选取两种不同的计算方法,请同学板书. 指出蕴含在探索活动过程中的“分类”、“化归”、“数形结合”等思想方法,体会实际问 题数学化的过程,感受体现在有理数运算中的对立统一规律. 练习 计算: 1.2 1 4 ×(- 6 7 )÷( 1 2 -2); 2.-1 2 3 ×(1- 2 3 )÷1 1 9 ; 3.[12-4×(3-10)]÷4. - 4 - 4.(1)-8-32÷(-4); (2)-9×(-2)-15÷(-3); (3)2-2÷ 1 2 ×2; (4)-3.5÷ 2 3 ×(- 3 4 ); (5)(-6)÷ 2 3 ÷ 3 4 . 同上. 三、交流反思 总结:通过这节课你学到了什么? 四、布置作业 课本 P48 习题 2.6 第 A:4、B:5 题.查看更多