北师版七年级数学上册-第五章检测题

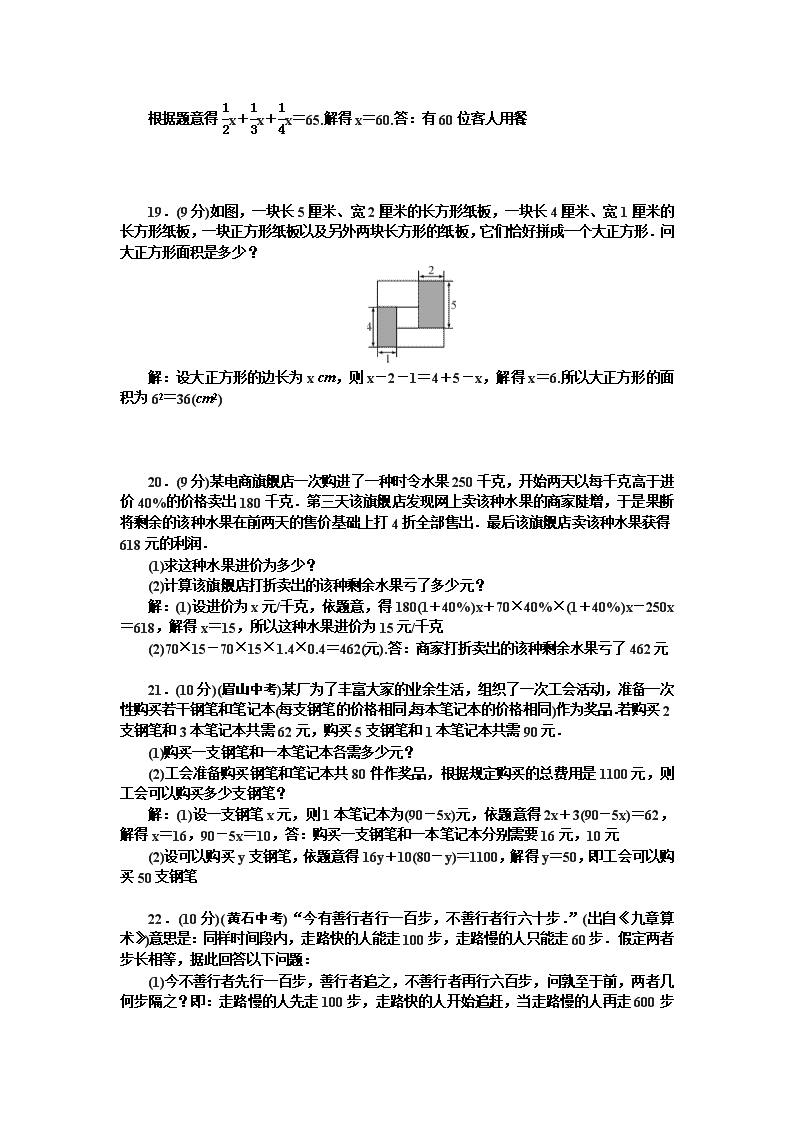
北师版七年级数学上册-第五章检测题

第五章检测题 (时间：100 分钟 满分：120 分) 一、选择题(每小题 3 分，共 30 分) 1．在方程 3x－y＝2，x＋1 x －2＝0，x－1 2 ＝1 2 ，x2－2x－3＝0，x＝2 中，一元一次方程 的个数为( B ) A．1 个 B．2 个 C．3 个 D．4 个 2．(怀化中考)一元一次方程 x－2＝0 的解是( A ) A．x＝2 B．x＝－2 C．x＝0 D．x＝1 3．若 2a＝3b，则下列各式中不成立的是( D ) A．4a＝6b B．2a＋5＝3b＋5 C．a 3 ＝b 2D．a＝2 3b 4．小明解方程 2(x－2)－3(4x－1)＝9(1－x)，在去括号时完全正确的是( B ) A．2x－2－12x－3＝9－9x B．2x－4－12x＋3＝9－9x C．2x－2－12x＋3＝9－9x D．2x－4－12x＋3＝9－x 5．解方程2y－1 4 －4y－3 6 ＝1 时，去分母正确的是( D ) A．6y－1－8y－3＝1 B．6y－1－8y－3＝12 C．6y－3－8y－6＝12 D．6y－3－8y＋6＝12 6．已知 x＝－2 是方程 5x＋12＝x 2 －a 的解，则 a2＋a－6 的值为( A ) A．0 B．6 C．－6 D．－18 7．(哈尔滨中考)某车间有 26 名工人，每人每天可以生产 800 个螺钉或 1000 个螺母，1 个螺钉需要配 2 个螺母，为使每天生产的螺钉和螺母刚好配套．设安排 x 名工人生产螺钉， 则下面所列方程正确的是( C ) A．2×1000(26－x)＝800x B．1000(13－x)＝800x C．1000(26－x)＝2×800x D．1000(26－x)＝800x 8．A，B 两地相距 900 千米，甲乙两车分别从 A，B 两地同时出发，相向而行，已知 甲车的速度为 110 千米/时，乙车的速度为 90 千米/时，则当两车相距 100 千米时，甲车行 驶的时间是( D ) A．4 小时 B．4.5 小时 C．5 小时 D．4 小时或 5 小时 9．(长沙中考)中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关， 初日健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是，有人要去某关口，路程 为 378 里，第一天健步行走，从第二天起，由于脚痛，每天走的路程都为前一天的一半， 一共走了六天才到达目的地，则此人第六天走的路程为( C ) A．24 里 B．12 里 C．6 里 D．3 里 10．如图，在长方形 ABCD 中，AB＝10 cm，BC＝6 cm，动点 P，Q 分别从点 A，B 同时出发，点 P 以 3 cm/s 的速度沿 AB，BC 向点 C 运动，点 Q 以 1 cm/s 的速度沿 BC 向 点 C 运动．设 P，Q 运动的时间是 t 秒，当点 P 与点 Q 重合时，t 的值是( C ) A.5 2 B．4 C．5 D．6 二、填空题(每小题 3 分，共 15 分) 11．(成都中考)若 m＋1 与－2 互为相反数，则 m 的值为__1__． 12．如果甲、乙两班共有 90 人，如果从甲班抽调 3 人到乙班，则甲、乙两班的人数相 等，则甲班原有__48__人. 13．(南通中考)《九章算术》是中国传统数学最重要的著作之一．书中记载：“今有人 共买鸡，人出九，盈十一；人出六，不足十六．问人数几何？”意思是：“有若干人共同出 钱买鸡，如果每人出九钱，那么多了十一钱；如果每人出六钱，那么少了十六钱．问：共 有几个人？”设共有 x 个人共同出钱买鸡，根据题意，可列一元一次方程为__9x－11＝6x ＋16__． 14．(毕节中考)某品牌旗舰店平日将某商品按进价提高 40%后标价，在某次电商购物节 中，为促销该商品，按标价 8 折销售，售价为 2240 元，则这种商品的进价是__2000__元． 15．(呼和浩特中考)关于 x 的方程 mx2m－1＋(m－1)x－2＝0 如果是一元一次方程，则其 解为__x＝2 或 x＝－2 或 x＝－3__． 三、解答题(共 75 分) 16．(8 分)解方程： (1)5x－7(1－x)＝－5； (2)1－3x＋7 8 ＝3x－10 4 －x； 解：x＝1 6 解：x＝21 (3)x－1 2[x－1 2(x＋1 2)]＝2. 解：x＝5 2 17．(9 分)若方程2x－3 5 ＝2 3x－2 与 3n－1 4 ＝3(x＋n)－2n 的解相同，求(n－3)2 的值． 解：解方程2x－3 5 ＝2 3x－2 得 x＝21 4 ，把 x＝21 4 代入 3n－1 4 ＝3(x＋n)－2n 得 n＝8，所以(n －3)2＝25 18．(9 分)《孙子算经》是我国传统数学的重要著作之一，其中记载的“荡杯问题”非 常有趣．原题是今有妇人河上荡杯，津吏问曰：“杯何以多？”妇人曰：“有客．”津吏曰： “客几何？”妇人曰：“两人共饭，三人共羹，四人共肉，凡用杯六十五．不知客几何？” 大意：一个妇女在河边洗碗，河官问：“洗多少碗？有多少客？”妇女答：“洗 65 只碗， 客人二人共用一只饭碗，三人共用一只汤碗，四人共用一只肉碗．问：有多少客人用餐？” 请解答上述问题. 解：设共有客人 x 人， 根据题意得 1 2x＋1 3x＋1 4x＝65.解得 x＝60.答：有 60 位客人用餐 19．(9 分)如图，一块长 5 厘米、宽 2 厘米的长方形纸板，一块长 4 厘米、宽 1 厘米的 长方形纸板，一块正方形纸板以及另外两块长方形的纸板，它们恰好拼成一个大正方形．问 大正方形面积是多少？ 解：设大正方形的边长为 x cm，则 x－2－1＝4＋5－x，解得 x＝6.所以大正方形的面 积为 62＝36(cm2) 20．(9 分)某电商旗舰店一次购进了一种时令水果 250 千克，开始两天以每千克高于进 价 40%的价格卖出 180 千克．第三天该旗舰店发现网上卖该种水果的商家陡增，于是果断 将剩余的该种水果在前两天的售价基础上打 4 折全部售出．最后该旗舰店卖该种水果获得 618 元的利润． (1)求这种水果进价为多少？ (2)计算该旗舰店打折卖出的该种剩余水果亏了多少元？ 解：(1)设进价为 x 元/千克，依题意，得 180(1＋40%)x＋70×40%×(1＋40%)x－250x ＝618，解得 x＝15，所以这种水果进价为 15 元/千克 (2)70×15－70×15×1.4×0.4＝462(元).答：商家打折卖出的该种剩余水果亏了 462 元 21．(10 分)(眉山中考)某厂为了丰富大家的业余生活，组织了一次工会活动，准备一次 性购买若干钢笔和笔记本(每支钢笔的价格相同，每本笔记本的价格相同)作为奖品．若购买 2 支钢笔和 3 本笔记本共需 62 元，购买 5 支钢笔和 1 本笔记本共需 90 元． (1)购买一支钢笔和一本笔记本各需多少元？ (2)工会准备购买钢笔和笔记本共 80 件作奖品，根据规定购买的总费用是 1100 元，则 工会可以购买多少支钢笔？ 解：(1)设一支钢笔 x 元，则 1 本笔记本为(90－5x)元，依题意得 2x＋3(90－5x)＝62， 解得 x＝16，90－5x＝10，答：购买一支钢笔和一本笔记本分别需要 16 元，10 元 (2)设可以购买 y 支钢笔，依题意得 16y＋10(80－y)＝1100，解得 y＝50，即工会可以购 买 50 支钢笔 22．(10 分)(黄石中考)“今有善行者行一百步，不善行者行六十步．”(出自《九章算术》) 意思是：同样时间段内，走路快的人能走 100 步，走路慢的人只能走 60 步．假定两者步长 相等，据此回答以下问题： (1)今不善行者先行一百步，善行者追之，不善行者再行六百步，问孰至于前，两者几 何步隔之？即：走路慢的人先走 100 步，走路快的人开始追赶，当走路慢的人再走 600 步 时，请问谁在前面，两人相隔多少步？ (2)今不善行者先行两百步，善行者追之，问几何步及之？即：走路慢的人先走 200 步， 请问走路快的人走多少步才能追上走路慢的人？ 解：(1)设当走路慢的人再走 600 步时，走路快的人的走 x 步，由题意得 x 600 ＝100 60 ，∴x ＝1000，∴1000－600－100＝300，答：当走路慢的人再走 600 步时，走路快的人在前面， 两人相隔 300 步 (2)设走路快的人走 y 步才能追上走路慢的人，由题意得 y＝200＋ 60 100y，∴y＝500，答： 走路快的人走 500 步才能追上走路慢的人 23．(11 分)(随州中考)我们知道，有理数包括整数、有限小数和无限循环小数，事实上， 所有的有理数都可以化为分数形式(整数可看作分母为 1 的分数)，那么无限循环小数如何表 示为分数形式呢？请看以下示例： 例：将 0.7 化为分数形式 由于 0.7＝0.777…，设 x＝0.777…①， 则 10x＝7.777…②， ②－①得 9x＝7，解得 x＝7 9 ，于是得 0.7＝7 9. 同理可得 0.3＝3 9 ＝1 3 ，1.4＝1＋0.4＝1＋4 9 ＝13 9 . 根据以上阅读，回答下列问题：(以下计算结果均用最简分数表示) 【基础训练】 (1)0.5＝________，5.8＝________； (2)将 0.23 化为分数形式，写出推导过程； 【能力提升】 (3)0.315＝________，2.018＝________； (注：0.315＝0.315315…，2.018＝2.01818…) 【探索发现】 (4)①试比较 0.9 与 1 的大小；0.9________1；(填“>”“<”或“＝”) ②若已知 0.285714＝2 7 ，则 3.714285＝________． (注：0.285714＝0.285714285714…) 解：(1)5 9 53 9 (2)0.23＝0.232323…，设 x＝0.232323…①，则 100x＝23.2323…②，②－①，得 99x＝ 23，解得 x＝23 99 ，∴0.23＝23 99 (3)同理 0.315＝315 999 ＝ 35 111 ，2.018＝2＋ 1 10 ×18 99 ＝111 55 ，故答案为： 35 111 111 55 (4)①0.9＝9 9 ＝1，故答案为：＝ ②∵3.714285＋0.285714＝3.9，又 0.285714＝2 7 ，0.9＝1，∴3.714285＝3.9－2 7 ＝3＋0.9 －2 7 ＝26 7