云南省玉溪一中2019届高三下学期第五次调研考试 数学（文）试题

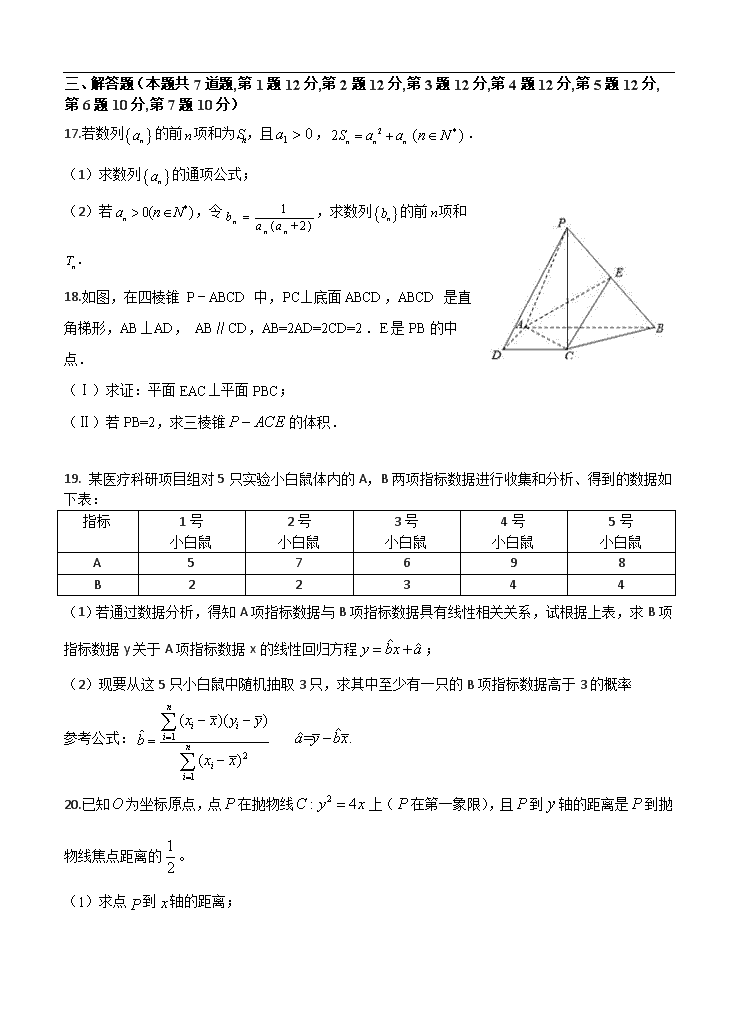
云南省玉溪一中2019届高三下学期第五次调研考试 数学（文）试题

玉溪一中第五次调研考试数学（文）试卷 考试时间：120分钟；‎ 注意事项：‎ 答题前填写好自己的姓名、班级、考号等信息,请将答案正确填写在答题卡上 第I卷（选择题）‎ 一、选择题（每题5分，共60分）‎ ‎1.若集合，，则（ ）‎ A．{1,2} B．[1,2] C．(1,2) D．‎ ‎2.已知i是虚数单位，复数z满足，则z的虚部是（ ）‎ A．1 B．i C．－1 D．－i ‎3.函数的图象与函数的图象的交点个数是( )‎ A．2 B．3 C．4 D．5 ‎ ‎4.若向量的夹角为，且，，则向量与向量的夹角为（ ）‎ A． B． C. D．‎ ‎5.已知，，若不等式恒成立，则m的最大值为（ ）‎ A．9 B．12 C．18 D．24 ‎ ‎6.已知，且，则等于（ ）‎ A． B． C． D．‎ ‎7.三棱柱ABC﹣A1B1C1的侧棱垂直于底面，且AB⊥BC，AB=BC=AA1=2，若该三棱柱的所有顶点都在同一球面上，则该球的表面积为（ ）‎ A．48π B．32π C．12π D．8π ‎8.设点是椭圆上异于长轴端点上的任意一点，分别是其左右焦点，‎ 为中心，，则此椭圆的离心率为（ ）‎ A． B． C. D．‎ ‎9.如图，网格纸上小正方形的边长为1，粗实线和粗虚线画出的是某多面体的三视图，则该多面体的体积为（ ）‎ A． B． C． D．‎ ‎10.已知是定义域为的奇函数，满足．若，则 ‎（ ）‎ A．－50 B． 0 C．2 D．50‎ ‎11.的内角的对边分别为，若，则（ ）‎ A．12 B．42 C．21 D．63‎ ‎12.设双曲线的左、右焦点分别为、。若点在双曲线右支上，且为锐角三角形，则的取值范围（ ） ‎ A． B． C． D．‎ 第II卷（非选择题）‎ 二、填空题（本题共4道小题，每小题5分，共20分）‎ ‎13.若实数满足则的最大值是 ．‎ ‎14.口袋内装有一些除颜色不同之外其它均相同的红球、白球和黑球，从中摸出1个球，摸出红球的概率是0．42，摸出白球的概率是0．28，若红球有21个，则黑球有___ ．‎ ‎15.在平面直角坐标系中，，求过点A与圆C： 相切的直线方程 ．‎ ‎16.已知函数，的四个根为，，，，且，则 ．‎ 三、解答题（本题共7道题,第1题12分,第2题12分,第3题12分,第4题12分,第5题12分,第6题10分,第7题10分）‎ ‎17.若数列的前项和为，且，．‎ ‎（1）求数列的通项公式；‎ ‎（2）若，令，求数列的前项和．‎ ‎18.如图，在四棱锥 P﹣ABCD 中，PC⊥底面ABCD，ABCD 是直角梯形，AB⊥AD， AB∥CD，AB=2AD=2CD=2．E是PB的中点．‎ ‎（Ⅰ）求证：平面EAC⊥平面PBC；‎ ‎（Ⅱ）若PB=2，求三棱锥的体积．‎ ‎19. 某医疗科研项目组对5只实验小白鼠体内的A，B两项指标数据进行收集和分析、得到的数据如下表：‎ 指标 ‎1号 小白鼠 ‎2号 小白鼠 ‎3号 小白鼠 ‎4号 小白鼠 ‎5号 小白鼠 A ‎5‎ ‎7‎ ‎6‎ ‎9‎ ‎8‎ B ‎2‎ ‎2‎ ‎3‎ ‎4‎ ‎4‎ ‎（1）若通过数据分析，得知A项指标数据与B项指标数据具有线性相关关系，试根据上表，求B项指标数据y关于A项指标数据x的线性回归方程；‎ ‎（2）现要从这5只小白鼠中随机抽取3只，求其中至少有一只的B项指标数据高于3的概率 参考公式： ‎ ‎20.已知为坐标原点，点在抛物线上（在第一象限），且到轴的距离是到抛物线焦点距离的。‎ ‎（1）求点到轴的距离；‎ ‎（2）过点的直线与抛物线有两个不同的交点，且直线交轴于点，直线交轴于点，且。求证：为定值。‎ ‎21.（本小题满分12分）‎ 设函数.‎ ‎（1）求的单调区间;‎ ‎（2）若，为整数，且当时，(x－k) f´(x)+x+1>0，求的最大值.‎ ‎22.选修4-4：坐标系与参数方程 在直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，并使得它与直角坐标系xOy有相同的长度单位，曲线C的极坐标方程为．‎ ‎（1）求直线l的普通方程和曲线C的直角坐标方程；‎ ‎（2）设曲线C与直线l交于A、B两点，且M点的坐标为(3,4)，求的值．‎ ‎23. 选修4-5：不等式选讲 已知函数.‎ ‎（1）求不等式的解集；‎ ‎（2）若存在实数满足，求实数a的最大值.‎ 玉溪一中第五次调研考试数学（文）试卷答案 第I卷（选择题）‎ 一、选择题（每题5分，共60分）‎ ‎1.若集合，，则（ A ）‎ A．{1,2} B．[1,2] C．(1,2) D．‎ ‎2.已知i是虚数单位，复数z满足，则z的虚部是（ A ）‎ A．1 B．i C．－1 D．－i ‎3.函数的图象与函数的图象的交点个数是( B )‎ A．2 B．3 C．4 D．5 ‎ ‎4.若向量的夹角为，且，，则向量与向量的夹角为（ A ）‎ A． B． C. D．‎ ‎5.已知，，若不等式恒成立，则m的最大值为（ B ）‎ A．9 B．12 C．18 D．24 ‎ ‎6.已知，且，则等于（ B ）‎ A． B． C． D．‎ ‎7.三棱柱ABC﹣A1B1C1的侧棱垂直于底面，且AB⊥BC，AB=BC=AA1=2，若该三棱柱的所有顶点都在同一球面上，则该球的表面积为（ C ）‎ A．48π B．32π C．12π D．8π ‎8.设点是椭圆上异于长轴端点上的任意一点，分别是其左右焦点，‎ 为中心，，则此椭圆的离心率为（ C ）‎ A． B． C. D．‎ ‎9.如图，网格纸上小正方形的边长为1，粗实线和粗虚线画出的是某多面体的三视图，则该多面体的体积为（ C ）‎ A． B． C． D．‎ ‎10. 已知是定义域为的奇函数，满足．若，则 ‎（ C ）‎ A. －50 B. 0 C. 2 D. 50‎ ‎11. 的内角的对边分别为，若，则（ C ）‎ A．12 B．42 C．21 D．63‎ ‎12.设双曲线的左、右焦点分别为、。若点在双曲线右支上，且为锐角三角形，则的取值范围（ D ） ‎ A． B． C． D．‎ 第II卷（非选择题）‎ 二、填空题（本题共4道小题，每小题5分，共20分）‎ ‎13.若实数满足则的最大值是 2 ．‎ ‎14. 口袋内装有一些除颜色不同之外其他均相同的红球、白球和黑球，从中摸出1‎ 个球，摸出红球的概率是0．42，摸出白球的概率是0．28，若红球有21个，则黑球有 15 ．‎ ‎15.在平面直角坐标系中，，求过点A与圆C：相切的直线方程 或 ．‎ ‎16.已知函数，的四个根为，，，，且，则 2 ．‎ 三、解答题（本题共7道题,第1题12分,第2题12分,第3题12分,第4题12分,第5题12分,第6题10分,第7题10分）‎ ‎17.若数列的前项和为，首项且．‎ ‎（1）求数列的通项公式；‎ ‎（2）若，令，求数列的前项和．‎ 解：（1）或；（2）．‎ 解析：（1）当时，，则 ‎ ‎ 当时，，‎ 即或 或 ‎ ‎（2）由，，‎ ‎ ‎ ‎18.如图，在四棱锥 P﹣ABCD 中，PC⊥底面ABCD，ABCD 是直角梯形，AB⊥AD， AB∥CD，AB=2AD=2CD=2．E是PB的中点．‎ ‎（Ⅰ）求证：平面EAC⊥平面PBC；‎ ‎（Ⅱ）若PB=2，求三棱锥的体积．‎ 解：（1）‎ ‎（2）‎ ‎19. 某医疗科研项目组对5只实验小白鼠体内的A，B两项指标数据进行收集和分析、得到的数据如下表：‎ 指标 ‎1号 小白鼠 ‎2号 小白鼠 ‎3号 小白鼠 ‎4号 小白鼠 ‎5号 小白鼠 A ‎5‎ ‎7‎ ‎6‎ ‎9‎ ‎8‎ B ‎2‎ ‎2‎ ‎3‎ ‎4‎ ‎4‎ ‎（1）若通过数据分析，得知A项指标数据与B项指标数据具有线性相关关系，试根据上表，求B项指标数据y关于A项指标数据x的线性回归方程；‎ ‎（2）现要从这5只小白鼠中随机抽取3只，求其中至少有一只的B项指标数据高于3的概率 参考公式： ‎ 解：（1）根据题意，计算 ‎，‎ ‎，所以线性回归方程为。‎ ‎（2）从这5只小白鼠中随机抽取三只，基本事件数为223,224,225,234,235,245，……，345‎ 共10种不同的取法，其中至少有一只B项指标数据高于3的基本事件共9种取法，‎ 所以所求概率为 ‎20.已知为坐标原点，点在抛物线上（在第一象限），且到轴的距离是到抛物线焦点距离的。‎ ‎（1）求点到轴的距离；‎ ‎（2）过点的直线与抛物线有两个不同的交点，且直线交轴于点，直线交轴于点，且。求证：为定值。‎ 解：（Ⅰ）因为抛物线y2=2px经过点P（1，2），‎ 所以4=2p，解得p=2，所以抛物线的方程为y2=4x．‎ 由题意可知直线l的斜率存在且不为0，‎ 设直线l的方程为y=kx+1（k≠0）．‎ 由得．‎ 依题意，解得k<0或00，求的最大值.‎ 解：‎ ‎（Ⅰ）的定义域为，。若，则，所以在内单调递增；若，则当时，，当时，，所以，在内单调递减，在内单调递增。......5分 ‎（Ⅱ）由，有，当时，(x－k) f´(x)+x+1>0等价于，（）......7分 令，则。由（Ⅰ）知，在内单调递增，而，，所以在内存在唯一的零点，故在内存在唯一的零点，设此零点为，则。.....10分 当时，；当时，，所以在内的最小值为，又有，可得，所以。‎ 所以。整数的最大取值为2。......12分 ‎22.选修4-4：坐标系与参数方程 在直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，并使得它与直角坐标系xOy有相同的长度单位，曲线C的极坐标方程为．‎ ‎（1）求直线l的普通方程和曲线C的直角坐标方程；‎ ‎（2）设曲线C与直线l交于A、B两点，且M点的坐标为(3,4)，求的值．‎ ‎（1）解：：，C：，即 ‎ 所以C 的普通方程是 ‎（2）解：将直线方程化为参数方程：‎ 带入C的普通方程得：，设A，B对应的参数分别是，，则，所以 ‎23.已知函数.‎ ‎（1）求不等式的解集；‎ ‎（2）若存在实数满足，求实数a的最大值.‎ 解：（1） ‎ 当时，由，得 当时，由，得 当时，由，得 所以不等式的解集为 ‎ ‎（2）.]‎ 依题意有，即 ‎ 解得 故的最大值为3‎ 欢迎访问“高中试卷网”——http://sj.fjjy.org