2018-2019学年海南省文昌中学高一下学期段考数学试题（解析版）

2018-2019学年海南省文昌中学高一下学期段考数学试题（解析版）

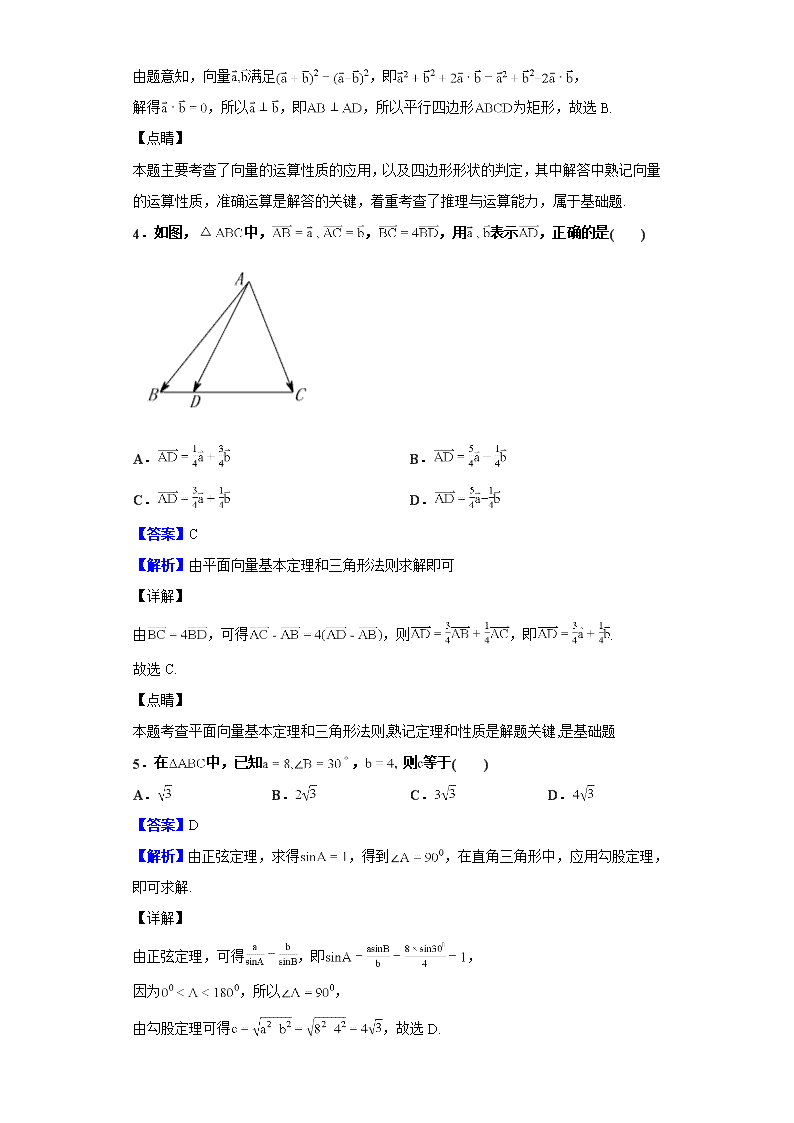
‎2018-2019学年海南省文昌中学高一下学期段考数学试题 一、单选题 ‎1．数列的第40项等于( )‎ A．9 B．10 C．40 D．41‎ ‎【答案】A ‎【解析】令，解得，即可求解，得到答案.‎ ‎【详解】‎ 由题意，数列，令，解得，‎ 所以数列的第40项是9，故选A.‎ ‎【点睛】‎ 本题主要考查了数列的通项公式的应用，其中解答中利用数列的通项公式，合理准确计算是解答的关键，着重考查了运算与求解能力，属于基础题.‎ ‎2．已知数列的一个通项公式为( )‎ A． B． C． D．‎ ‎【答案】B ‎【解析】把数列，化简为，利用归纳法，即可得到数列的一个通项公式，得到答案.‎ ‎【详解】‎ 由题意，数列，可化为，所以数列的一个通项公式为，故选B.‎ ‎【点睛】‎ 本题主要考查了利用归纳法求解数列的通项公式，其中解答中把数列，化简为，合理归纳是解答的关键，着重考查了运算与求解能力，属于基础题.‎ ‎3．在平行四边形中，，则当时，该平行四边形为( )‎ A．菱形 B．矩形 C．正方形 D．以上都不正确 ‎【答案】B ‎【解析】由，根据向量的运算，求得，得到，即，即可得到答案.‎ ‎【详解】‎ 由题意知，向量满足，即，‎ 解得，所以，即，所以平行四边形为矩形，故选B.‎ ‎【点睛】‎ 本题主要考查了向量的运算性质的应用，以及四边形形状的判定，其中解答中熟记向量的运算性质，准确运算是解答的关键，着重考查了推理与运算能力，属于基础题.‎ ‎4．如图，中，，，用表示，正确的是( )‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】由平面向量基本定理和三角形法则求解即可 ‎【详解】‎ 由，可得，则，即.‎ 故选C.‎ ‎【点睛】‎ 本题考查平面向量基本定理和三角形法则,熟记定理和性质是解题关键,是基础题 ‎5．在中，已知，则等于( )‎ A． B． C． D．‎ ‎【答案】D ‎【解析】由正弦定理，求得，得到，在直角三角形中，应用勾股定理，即可求解.‎ ‎【详解】‎ 由正弦定理，可得，即，‎ 因为，所以，‎ 由勾股定理可得，故选D.‎ ‎【点睛】‎ 本题主要考查了正弦定理的应用，以及直角三角形的勾股定理的应用，其中解答中利用正弦定理求得是解答本题关键，着重考查了运算与求解能力，属于基础题.‎ ‎6．在中，若，则的形状是( )‎ A．钝角三角形 B．直角三角形 C．锐角三角形 D．不能确定 ‎【答案】A ‎【解析】由正弦定理得，再由余弦定理求得，得到，即可得到答案.‎ ‎【详解】‎ 因为在中，满足，‎ 由正弦定理知，代入上式得，‎ 又由余弦定理可得，因为C是三角形的内角，所以，‎ 所以为钝角三角形，故选A.‎ ‎【点睛】‎ 本题主要考查了利用正弦定理、余弦定理判定三角形的形状，其中解答中合理利用正、余弦定理，求得角C的范围是解答本题的关键，着重考查了推理与运算能力，属于基础题.‎ ‎7．已知数列{}满足，，则( )‎ A．53 B．54 C．55 D．109‎ ‎【答案】C ‎【解析】由数列满足，即，利用递推关系，即可求解得值，得到答案.‎ ‎【详解】‎ 由题意知，数列满足，即，‎ 所以 ‎ ‎，‎ 又由，所以，故选C.‎ ‎【点睛】‎ 本题主要考查了数列的递推公式的应用，其中解答中熟练应用数列的递推关系式，准确计算是解答的关键，着重考查了运算与求解能力，属于基础题.‎ ‎8．已知非零单位向量满足，则与的夹角是( )‎ A． B． C． D．‎ ‎【答案】D ‎【解析】由题意利用两个向量的加减法及其几何意义，可得，利用向量的夹角公式，即可求解，得到答案.‎ ‎【详解】‎ 因为非零单位向量满足，‎ 所以，整理得，所以，‎ 则，，，‎ 所以向量与的夹角，‎ 又因为，所以，故选D.‎ ‎【点睛】‎ 本题主要考查了向量的数量积的运算，以及向量的夹角公式的应用，其中解答中根据向量的数量积的运算，求得，再利用向量的夹角公式求解是解答的关键，着重考查了运算与求解能力，属于基础题.‎ ‎9．《周碑算经》中有这样一个问题：从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种这十二个节气其日影长依次成等差数列,冬至、立春、春分日影长之和为31.5尺,前九个节气日影长之和为85.5尺,则小满日影长为( )‎ A．1.5尺 B．2.5尺 C．3.5尺 D．4.5尺 ‎【答案】B ‎【解析】设各节气日影长依次成等差数列，是其前项和，则===85.5，所以=9.5，由题知==31.5，所以=10.5，所以公差=−1，所以==2.5，故选B．‎ ‎10．如图，从气球上测得正前方的河流的两岸的俯角分别为，此时气球的高度是，则河流的宽度( )‎ A． B． C． D．‎ ‎【答案】C ‎【解析】由题意画出示意图，由两角差的正切求出得正切值，然后通过求解两个直角三角形得到DC和DB的长度，即可求解，得到答案.‎ ‎【详解】‎ 如图所示，，‎ 又由，‎ 在直角中，，所以，‎ 在直角中，，所以，‎ 所以 ，故选C.‎ ‎【点睛】‎ 本题主要考查了解三角形的实际应用问题，其中解答中画出示意图，合理利用三角恒等变换的公式，以及直角三角形的性质是解答本题的关键，着重考查了推理与运算能力，属于基础题.‎ ‎11．在中，，，为的中点，将向量绕点按逆时针方向旋转得向量，则向量在向量方向上的投影为（ ）‎ A．-1 B．1 C． D．‎ ‎【答案】C ‎【解析】如图，以为轴建立平面直角坐标系，‎ 则，且，‎ 所以向量在向量方向上的投影为.‎ 本题选择C选项.‎ ‎12．已知是等差数列的前项和,且,给出下列五个命题:①；②；③；④数列中最大项为；⑤，其中正确命题的个数是( )‎ A．1 B．3 C．4 D．5‎ ‎【答案】B ‎【解析】由已知可得，，由此逐项判定，即可求解，得到答案.‎ ‎【详解】‎ 由题意，在等差数列中，满足，‎ 所以可得，所以，所以①正确；‎ 又由，所以②正确；‎ 又由，则，所以③不正确；‎ 由，所以数列为递减数列，且，‎ 可得数列中，当时，，当时，，‎ 所以数列前6项和最大，所以④不正确；‎ 由，即，所以⑤正确；‎ 故选B.‎ ‎【点睛】‎ 本题主要考查了等差数列的性质的综合应用，其中解答中熟练应用等差数列的性质和前n项和公式，逐项判定是解答的关键，着重考查了推理与运算能力，属于基础题.‎ 二、填空题 ‎13．已知，，且，则实数__________．‎ ‎【答案】‎ ‎【解析】由题意，，由，得，解得.‎ ‎【点睛】设向量，， 向量平行的两种方法：‎ ‎（1）的充要条件是；‎ ‎（2）不妨设，的充要条件是存在实数，使，即.‎ 第一种方法纯粹地是代数方程，第二种方法是几何方法，对不是坐标表示的向量平行非常适用.‎ ‎14．已知为等差数列，若 ，则________．‎ ‎【答案】1‎ ‎【解析】根据题设条件，求得，得到，即可求得，得到答案.‎ ‎【详解】‎ 由题意，数列为等差数列，且，‎ 根据等差数列的性质，可得，所以，‎ 所以.‎ ‎【点睛】‎ 本题主要考查了等差数列的性质的应用，以及特殊角的三角函数值，其中解答熟练应用等差数列的性质是解答的关键，着重考查了推理与运算能力，属于基础题.‎ ‎15．的内角的对边分别为，若，则 ________．‎ ‎【答案】 ‎ ‎【解析】根据正弦定理将边化为角，再根据两角和正弦公式以及诱导公式化简得cosB的值，即得B角.‎ ‎【详解】‎ 由2bcosB＝acosC＋ccosA及正弦定理，得2sinBcosB＝sinAcosC＋sinCcosA.‎ ‎∴2sinBcosB＝sin(A＋C)．‎ 又A＋B＋C＝π，∴A＋C＝π－B.∴2sinBcosB＝sin(π－B)＝sinB.‎ 又sinB≠0，∴cosB＝.∴B＝.‎ ‎∵在△ABC中，acosC＋ccosA＝b，∴条件等式变为2bcosB＝b，∴cosB＝.‎ 又0

查看更多