人教A版高中数学3-2-2函数模型的应用举例（2）教案新人教版必修1

人教A版高中数学3-2-2函数模型的应用举例（2）教案新人教版必修1

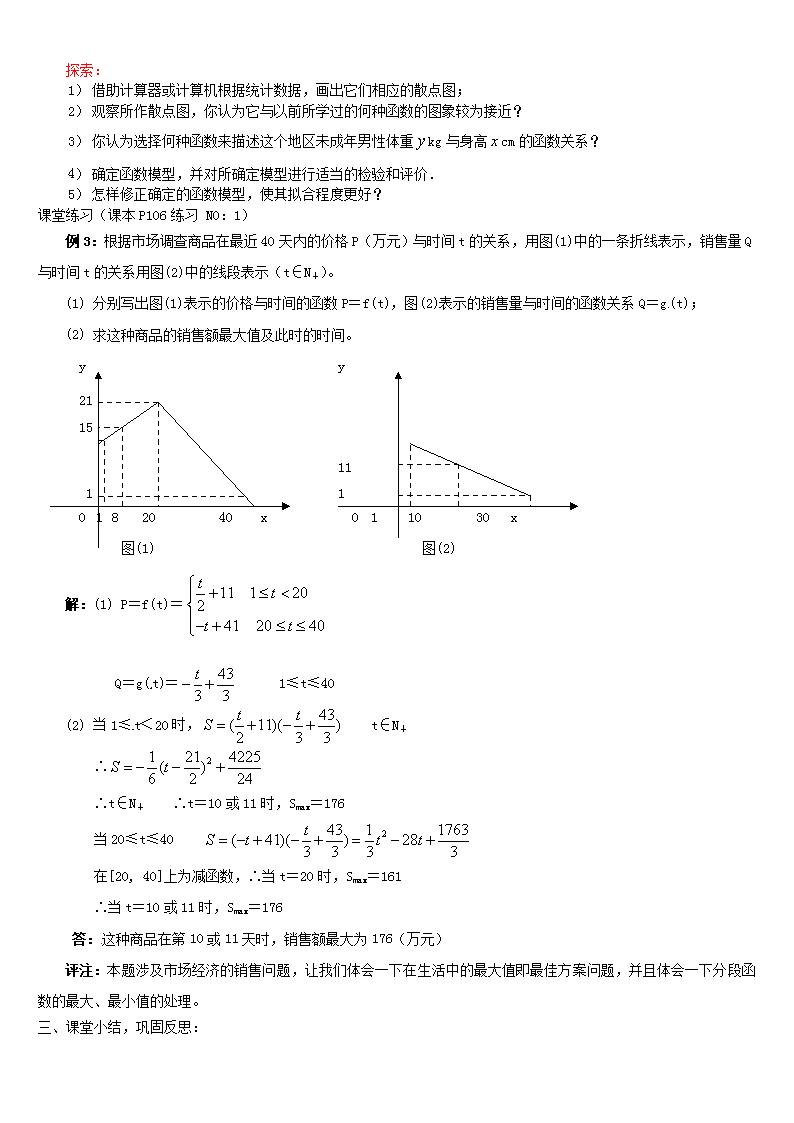
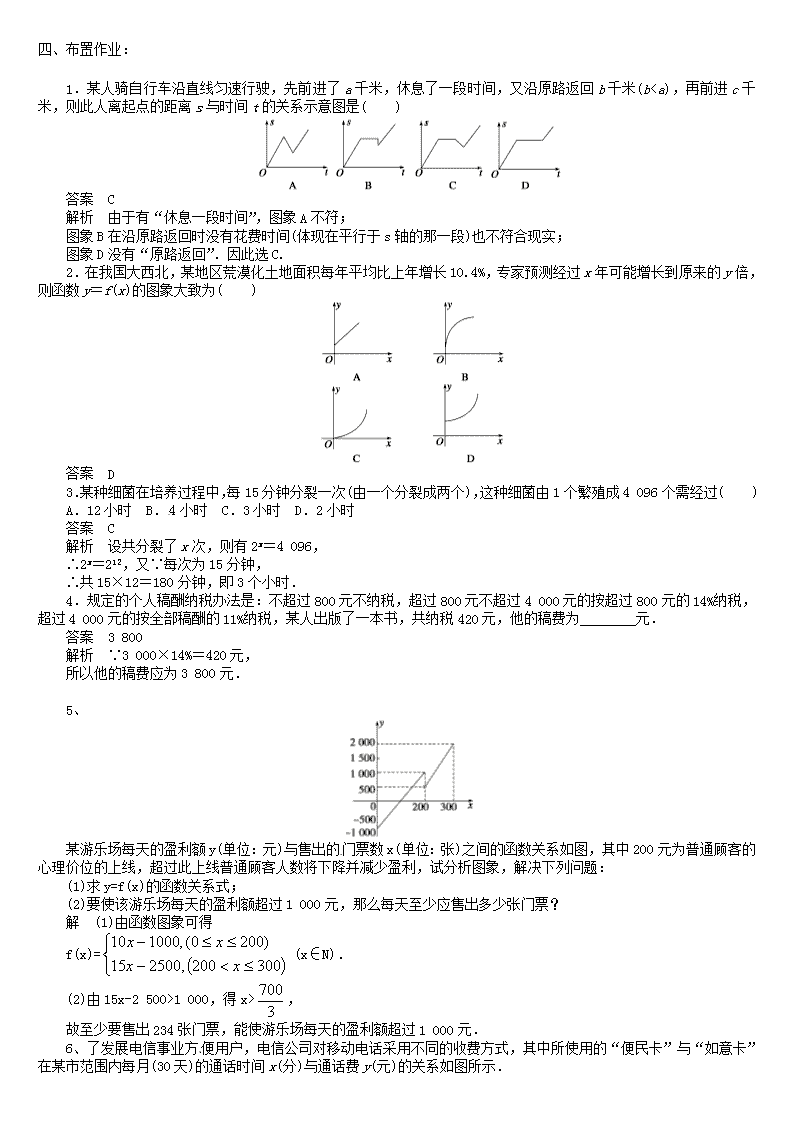
3.2.2（2）函数模型的应用实例（教学设计） 教学目标： 知识与技能：能够找出简单实际问题中的函数关系式，初步体会应用一次函数、二次函数模型解决实际问题． 过程与方法：感受运用函数概念建立模型的过程和方法，体会一次函数、二次函数模型在数学和其他学科中的重 要性． 情感、态度、价值观：体会运用函数思想和处理现实生活和社会中的简单问题的实用价值． 教学重点难点： 重点 运用一次函数、二次函数模型的处理实际问题． 难点 运用函数思想理解和处理现实生活和社会中的简单问题． 一、新课引入： 2003 年 5 月 8 日，西安交通大学医学院紧急启动“建立非典流行趋势预测与控制策略数学模型”研究项目．67 岁 的马知恩教授率领一批专家昼夜攻关，于 5 月 19 日初 步完成了第一批成果，并制成了可供决策部门参考的应用软件． 这一数学模型利用实际数据拟合参数，并对全国和北京、山西等地的疫情进行了计算仿真．结果指出，将患者及时 隔离对于抗击非典至关重要．分析报告说，就全国而论，若非典病人延迟隔离 1 天，就医人数将增加 1000 人左右，推 迟两天约增加 2100 人左右；若外界输入 1000 人中包含一个病人和一个潜伏病人，将增加患病人数 100 人左右；若 4 月 21 日以后，政府未采取隔离措施，则高峰期病人人数将达 60 万人． 这项研究在充分考虑传染病的一般流行机制、非典的特殊性、我国政府所采取的一系列强有力措施的基础上， 根据疾病控制中心每日发布的数据，利用统计学的方法和流行病传播机理建立了非典流行趋势预测动力学模型和 优化控制模型，并对非典未来的流行趋势做了分析预测． 二、师生互动，新课讲解： 例 1：（课本第 104 页例 5）某桶装水经营部每天的房租、人员工资等固定成本为 200 元，每桶水的进价是 5 元， 销售单价与日均销售量的关系如下表所示， 销售单价/元 6 7 8 9 10 11 12 日均销售量/桶 480 440 400 360 320 280 240 请根据以上数据作出分析，这个经营部怎样定价才能获得最大利润？ 解：（课本 P104） 课本第 104 页表 3-9 中数据的变化是有特定规律的，教学时应注意引导学生分析问题所提供的数据特点，由 数据特点抽象出函数模型．同时，应注意变量的变化范围，并以此检验结果的合理性． 例 2：（课本第 105 页例 6）某地区不同身高的未成年男性的体重平均值如下表： （身高：cm；体重：kg） 身高 60 70 80 90 100 110 体重 6.13 7.90 9.99 12.1 5 15.0 2 17.5 0 身高 120 130 140 150 160 170 体重 20.9 2 26.8 6 31.1 1 38.8 5 47.2 5 55.0 5 1）根据表中提供的数据，能否建立恰当的函数模型，使它能比较近似地反映这个地区未成年男性体重 y kg 与身高 x cm 的函数关系？试写出这个函数模型的解析式． 2）若体重超过相同身高男性体重平均值的 1.2 倍为偏胖，低于 0.8 倍为偏瘦，那么这个地区一名身高为 175cm， 体重为 78kg 的在校男生的体重是否正常？ 探索： 1） 借助计算器或计算机根据统计数据，画出它们相应的散点图； 2） 观察所作散点图，你认为它与以前所学过的何种函数的图象较为接近？ 3） 你认为选择何种函数来描述这个地区未成年男性体重 y kg 与身高 x cm 的函数关系？ 4） 确定函数模型，并对所确定模型进行适当的检验和评价． 5） 怎样修正确定的函数模型，使其拟合程度更好？ 课堂练习（课本 P106 练习 NO：1） 例 3：根据市场调查商品在最近 40 天内的价格 P（万元）与时间 t 的关系，用图(1)中的一条折线表示，销售量 Q 与时间 t 的关系用图(2)中的线段表示（t∈N＋）。 (1) 分别写出图(1)表示的价格与时间的函数 P＝f(t)，图(2)表示的销售量与时间的函数关系 Q＝g(t)； (2) 求这种商品的销售额最大值及此时的时间。 y y 21 15 11 1 1 0 1 8 20 40 x 0 1 10 30 x 图(1) 图(2) 解：(1) P＝f(t)＝ 11 1 202 41 20 40 t t t t         　　 　　 Q＝g(t)＝ 43 3 3 t  1≤t≤40 (2) 当 1≤t＜20 时， 43( 11)( )2 3 3 t tS     t∈N＋ ∴ 21 21 4225( )6 2 24S t    ∴t∈N＋ ∴t＝10 或 11 时，Smax＝176 当 20≤t≤40 243 1 1763( 41)( ) 283 3 3 3 tS t t t        在[20, 40]上为减函数，∴当 t＝20 时，Smax＝161 ∴当 t＝10 或 11 时，Smax＝176 答：这种商品在第 10 或 11 天时，销售额最大为 176（万元） 评注：本题涉及市场经济的销售问题，让我们体会一下在生活中的最大值即最佳方案问题，并且体会一下分段函 数的最大、最小值的处理。 三、课堂小结，巩固反思： 四、布置作业： 1．某人骑自行车沿直线匀速行驶，先前进了 a 千米，休息了一段时间，又沿原路返回 b 千米(b1 000，得 x> 3 700 ， 故至少要售出 234 张门票，能使游乐场每天的盈利额超过 1 000 元． 6、了发展电信事业方 便用户，电信公司对移动电话采用不同的收费方式，其中所使用的“便民卡”与“如意卡” 在某市范围内每月(30 天)的通话时间 x(分)与通话费 y(元)的关系如图所示． (1)分别求出通话费 y1，y2 与通话时间 x 之间的函数关系式； (2)请帮助用户计算，在一个月内使用哪种卡便宜． 解 (1)由图象可设 y1＝k1x＋29，y2＝k2x， 把点 B(30,35)，C(30,15)分别代入 y1，y2 得 k1＝1 5 ，k2＝1 2 . ∴y1＝1 5 x＋29，y2＝1 2 x. (2)令 y1＝y2，即 1 5 x＋29＝1 2 x，则 x＝962 3 . 当 x＝96 2 3 时，y1＝y2，两种卡收费一致； 当 x<96 2 3 时，y1>y2，即如意卡便宜； 当 x>96 2 3 时，y1

查看更多