数学人教B版必修4教案:1-3-1 正弦函数的图象与性质4 Word版
正弦型函数的图像变换教学设计
一、教学目标:
知识与技能目标:
能借助计算机课件,通过探索、观察参数 A、ω、φ对函数图象的影响,并能概括出三
角函数图象各种变换的实质和内在规律;会用图象变换画出函数 y=Asin(ωx+φ)的图象。
过程与方法目标:
通过对探索过程的体验,培养学生的观察能力和探索问题的能力,数形结合的思想;
领会从特殊到一般,从具体到抽象的思维方法,从而达到从感性认识到理性认识的飞跃。
情感、态度价值观目标:
通过学习过程培养学生探索与协作的精神,提高合作学习的意识。
二、教学重点:
考察参数ω、φ、A 对函数图象的影响,理解由 y=sinx 的图象到 y=Asin(ωx+φ)的图
象变化过程。
三、教学难点:
对 y=Asin(ωx+φ)的图象的影响规律的发现与概括是本节课的难点。
四、教学过程:整个教学过程是“以问题为载体,以学生活动为主线”进行的。
(一)创设情境:
1.视频演示: 《观览车》
观览车与我们学习的正弦函数有何关系?
【设计意图】直接切入研究的课题。(板书课题:正弦型函数 的图象)
介绍:振幅 周期 频率 相位 初相,使学生对 A w 有初步印象。
(二)新课引入
在预习学案上已完成
1.用五点法在同一坐标系中作函数 y=sinx+2 和 y=sinx-2 简图,并观察其图像可以由
y=sinx 图像如何得到?
2. 用五点法在同一坐标系中作函数 y=sin(x+
3
)和 y=sin(x-
3
)简图,并观察其
图像可以由 y=sinx 图像如何得到?
3. 用五点法在同一坐标系中作函数 y=2sinx 和 y=
2
1 sinx 简图,并观察其图像可以由
y=sinx 图像如何得到?
4. 用五点法在同一坐标系中作函数 y=sin2x 和 y=sin
2
1 x 简图,并观察其图像可以由
y=sinx 图像如何得到?
依次由学生上台展示列表与所作图像,并说明图像与 y=sinx 图像的关系,教师通过
PPT 动画及几何画板向学生展示一般规律,共同总结出
1. y=sinx y=sinx+b
y=sinx+b 的图象是由 y=sinx 的图象向上或向下平移∣b∣个单位而成
2. y=sinx y=sin(x+ )
y=sin(x+)的图象是由 y=sinx 的图象向左或向右平移 个单位而成.
3. y=sinx y=Asinx
y=Asinx,x∈R (A>0 且 A≠1) 的图象可以看作把正弦曲线上的所有点的纵坐标伸长
(A>1)或缩短 (0
0 且ω≠1) 的图象可以看作把正弦曲线上的所有点的横坐
标缩短(ω>1)或伸长(0<ω<1)到原来的 1/ω倍 (纵坐标不变)得到的 .
【设计意图】特殊到一般的学习方法比较符合学生的认知规律,同时也培养了学生抽象
概括能力。由于在高一上学期函数部分进行过较多的图象平移类变换,所以这部分内容不难,
老师可以让学生自主探究得到结论。只不过在叙述结论的时候,学生的语言可能不规范,易
出现如“把图象进行平移”的描述,教师可指出精确的描述应为:把“图象上的每一点”进
行平移)
重点总结 A w 在图像变换中的作用。如下图:
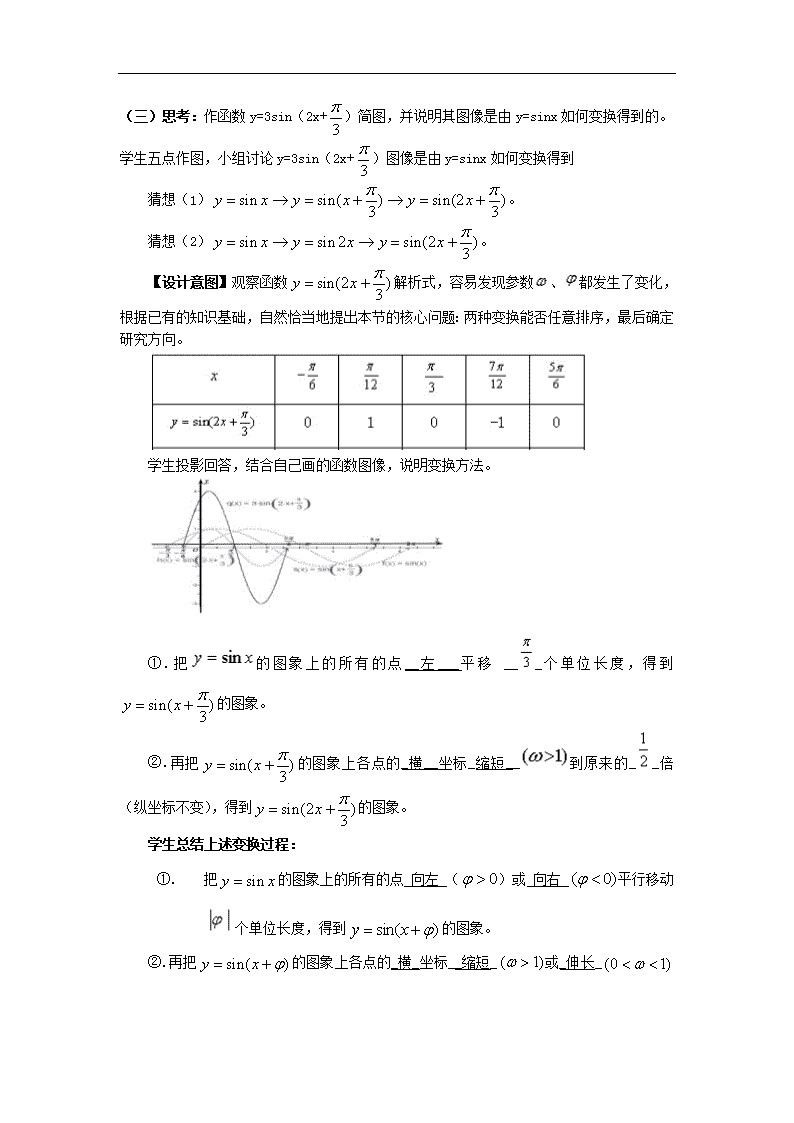
(三)思考:作函数 y=3sin(2x+
3
)简图,并说明其图像是由 y=sinx 如何变换得到的。
学生五点作图,小组讨论 y=3sin(2x+
3
)图像是由 y=sinx 如何变换得到
猜想(1) sin sin( ) sin(2 )3 3y x y x y x 。
猜想(2) sin sin2 sin(2 )3y x y x y x 。
【设计意图】观察函数 sin(2 )3y x 解析式,容易发现参数 、 都发生了变化,
根据已有的知识基础,自然恰当地提出本节的核心问题:两种变换能否任意排序,最后确定
研究方向。
学生投影回答,结合自己画的函数图像,说明变换方法。
① . 把 的 图 象 上 的 所 有 的 点 __ 左 ___ 平 移 __ _ 个 单 位 长 度 , 得 到
sin( )3y x 的图象。
②.再把 sin( )3y x 的图象上各点的_横__坐标_缩短__ 到原来的_ _倍
(纵坐标不变),得到 sin(2 )3y x 的图象。
学生总结上述变换过程:
1 . 把 siny x 的图象上的所有的点 向左 ( 0 )或 向右 ( 0) 平行移动
个单位长度,得到 sin( )y x 的图象。
②.再把 sin( )y x 的图象上各点的_横_坐标__缩短_ ( 1) 或_伸长_ (0 1)
到原来的_ _倍(_纵_坐标不变),得到 sin( )y x 的图象。
B、 深入探究,讨论分析:
第二种变换方法,平移量是 ,还是 ,为什么?
【设计意图】这部分内容是本堂课的难点,突破的方法先是从直观的“形”上“粉碎”
了学生错误的直觉,使学生“一惊”!渴望知道个中原因使他们积极探寻,当最终发现可以
用已有的知识来解释时,又让他们“一喜”,这“形”中的直观和“数”中的严谨,让学生
在“一惊一喜”中达到一悟皆通的效果。
学生总结第二种变换的规律:
把 y=sin ω x 的 图 象 上 的 所 有 的 点 向 左 ( 0) 或 向 右 ( 0) 平 行 移 动
| |( 0) 个单位长度,得到 y=sin(ωx+φ)的图象。
对比两种变换过程说明:先相位变换后周期变换平移 个单位长度。先周期变换后
相位变换平移 | |( 0) 个单位长度。
【设计意图】使学生由正弦曲线变化得到函数 y=Asin(ωx+φ)(A>0,ω>0)的图象的不
同方案有一个整体的认识,并在掌握图象变化实质的基础上,择优选择。
通 过 上 述 问 题 的 讨 论 与 研 究 , 如 何 由 正 弦 曲 线 通 过 图 像 变 换 得 到 函 数
sin( )y A x 的图像 ?
图像变换规律总结:
sin( )( 0, 0)y A x A 的图像可由 siny x 的图像经过如下变换得到:
方法一:
1
0) 0)
| |sin sin( )
sin( ) sin x )
y x y x
y x y A
横坐标变为原来的 倍向左( 或向右(
平移 个单位 纵坐标不变
纵坐标变为原来的A倍
横坐标不变 (
方法二:
1
0) 0)
| |
sin sin
sin( ) sin x )
y x y x
y x y A
横坐标变为原来的 倍 向左( 或向右(
纵坐标不变 平移 个单位
纵坐标变为原来的A倍
横坐标不变 (
【设计意图】组织学生进行讨论,学生通过自己作图,教师几何画板演示,进一步认识
有 siny x 经图象变换得到 sin( )y A x 的方法,并体会有简单到复杂、特殊到一
般的化归思想。
(四)课堂总结
(五)当堂检测
试一试:
不画图,说明下列函数的图像可由 y=sinx 的图像经过怎样的变换得到:
1.y=5sinx
2.y=sin x4
1
3.y=sin(x-
3
)
4.y= 2sin(x+
6
)
5.y=3sin(2x+
3
)
(六)作业:
课本 49 页 1、2 题