专题03 不等式与线性规划(仿真押题)-2017年高考数学(文)命题猜想与仿真押题
1.已知a,b,c满足c<b<a且ac<0,则下列选项中不一定能成立的是( )
A.< B.>0
C.< D.<0
【答案】:C
【解析】:∵c
0,∴<,>0,<0,
但b2与a2的关系不确定,故<不一定成立.
2.已知不等式ax2-bx-1≥0的解集是,则不等式x2-bx-a<0的解集是( )
A.(2,3)
B.(-∞,2)∪(3,+∞)
C.
D.∪
【答案】:A
【解析】:依题意,-与-是方程ax2-bx-1=0的两根,则即又a<0,不等式x2-bx-a<0可化为x2-x-1>0,即-x2+x-1>0,解得20在区间上有解,则实数a的取值范围为( )
A. B.
C.(1,+∞) D.(-∞,-1)
【答案】:A
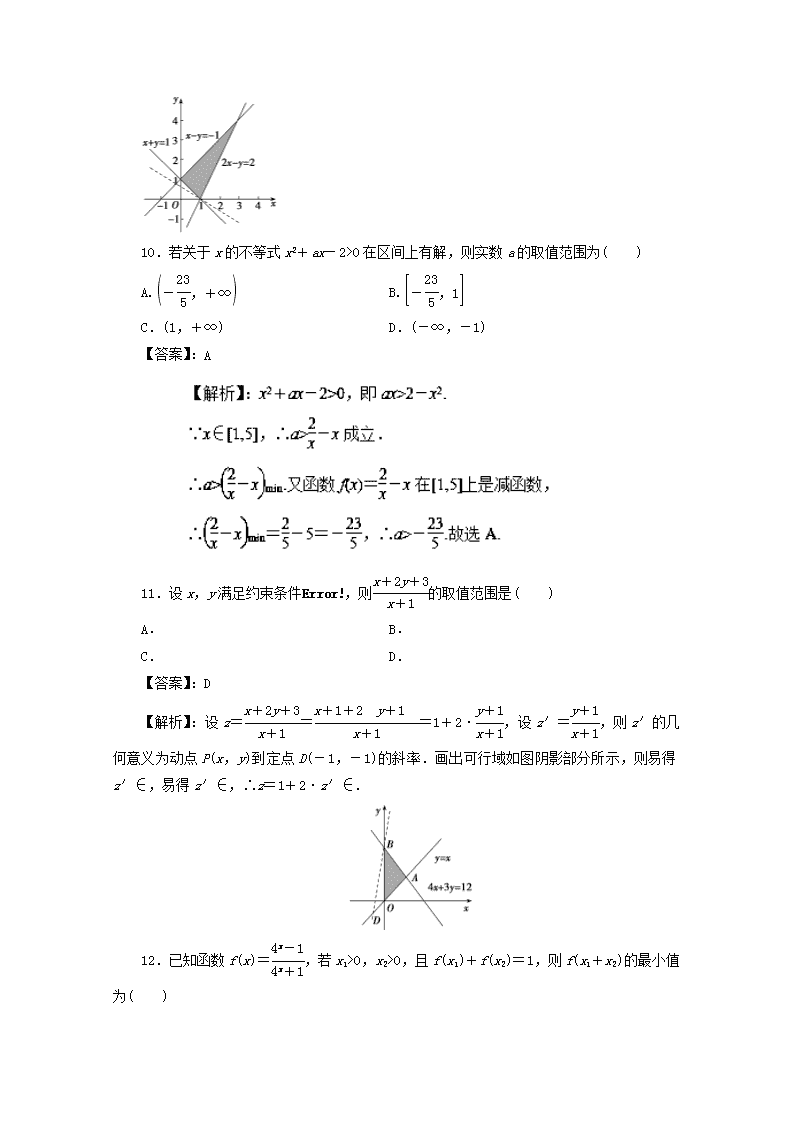
11.设x,y满足约束条件,则的取值范围是( )
A. B.
C. D.
【答案】:D
【解析】:设z===1+2·,设z′=,则z′的几何意义为动点P(x,y)到定点D(-1,-1)的斜率.画出可行域如图阴影部分所示,则易得z′∈,易得z′∈,∴z=1+2·z′∈.
12.已知函数f(x)=,若x1>0,x2>0,且f(x1)+f(x2)=1,则f(x1+x2)的最小值为( )
A. B.
C.2 D.4
【答案】:B
【解析】:由题意得f(x)==1-,由f(x1)+f(x2)=1得2--=1,化简得4-3=4+4≥2×2,解得2x1+x2≥3,所以f(x1+x2)=1-≥1-=.故选B.
13.已知a,b都是正实数,且2a+b=1,则+的最小值是________.
【答案】:8
【解析】:+=(2a+b)=4++≥4+2=8,当且仅当=,即a=,b=时,“=”成立,故+的最小值是8.
14.对于实数x,当且仅当n≤x
查看更多