理科立体几何高考题

理科立体几何高考题

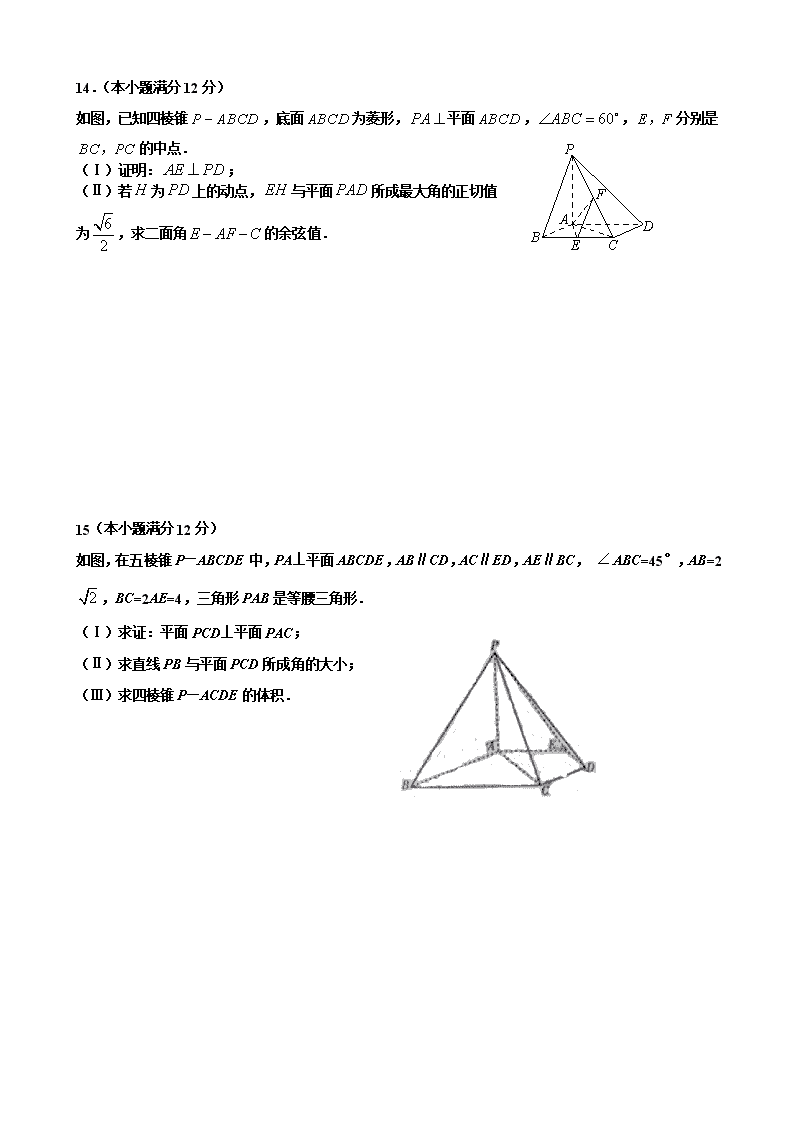
立体几何高考题 ‎1.在空间，下列命题正确的是 ‎（A）平行直线的平行投影重合（B）平行于同一直线的两个平面平行 ‎（C）垂直于同一平面的两个平面平行（D）垂直于同一平面的两条直线平行 ‎2.正方体ABCD-中，B与平面AC所成角的余弦值为 ‎（A） （B） （C） （D）‎ 俯视图 正(主)视图 侧(左)视图 ‎2‎ ‎3‎ ‎2‎ ‎2‎ ‎3．右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）‎ A． B． ‎ C． D．‎ ‎4.已知正四棱锥中，，那么当该棱锥的体积最大时，它的高为 ‎（A）1 （B） （C）2 （D）3‎ ‎5．已知正四棱锥的侧棱长与底面边长都相等，是的中点，则所成的角的余弦值为（ ）‎ A． B． C． D．‎ ‎6.与正方体的三条棱、、所在直线的距离相等的点 ‎（A）有且只有1个 （B）有且只有2个 ‎（C）有且只有3个 （D）有无数个 ‎7.已知在半径为2的球面上有A、B、C、D四点，若AB=CD=2,则四面体ABCD的体积的最大值为 ‎(A) (B) (C) (D) ‎ ‎8.已知三棱柱的侧棱与底面边长都相等，在底面内的射影为的中心，则与底面所成角的正弦值等于（ c ）‎ A． B． C． D．‎ ‎9.已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ ）‎ A．1 B． C． D．2‎ ‎10.等边三角形与正方形有一公共边，二面角的余弦值为，分别是的中点，则所成角的余弦值等于 ．‎ ‎11．平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：‎ 充要条件① ；‎ 充要条件② ．‎ ‎12．（本小题满分12分）‎ 四棱锥中，底面为矩形，侧面底面，，，．‎ ‎（Ⅰ）证明：；‎ ‎（Ⅱ）设与平面所成的角为，求二面角的大小．‎ C D E A B 13．（本小题满分12分）‎ 如图，正四棱柱中，，点在上且．‎ A B C D E A1‎ B1‎ C1‎ D1‎ ‎（Ⅰ）证明：平面；（Ⅱ）求二面角的大小．‎ ‎14．（本小题满分12分）‎ P B E C D F A 如图，已知四棱锥，底面为菱形，平面，，分别是的中点．‎ ‎（Ⅰ）证明：；‎ ‎（Ⅱ）若为上的动点，与平面所成最大角的正切值 为，求二面角的余弦值．‎ ‎15（本小题满分12分）‎ 如图，在五棱锥P—ABCDE中，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC， ABC=45°，AB=2，BC=2AE=4，三角形PAB是等腰三角形．‎ ‎（Ⅰ）求证：平面PCD⊥平面PAC；‎ ‎（Ⅱ）求直线PB与平面PCD所成角的大小；‎ ‎（Ⅲ）求四棱锥P—ACDE的体积．‎ ‎16如图，直三棱柱中，，，为的中点，为上的一点，．‎ ‎（Ⅰ）证明：为异面直线与的公垂线；‎ ‎（Ⅱ）设异面直线与的夹角为45°，求二面角的大小．‎ ‎17（本小题满分12分）‎ 如图，四棱锥S-ABCD中，SD底面ABCD，‎ AB//DC，ADDC，AB=AD=1，DC=SD=2，E为 棱SB上的一点，平面EDC平面SBC .‎ ‎（Ⅰ）证明：SE=2EB；‎ ‎（Ⅱ）求二面角A-DE-C的大小 .‎