历年四川卷数学高考题部分

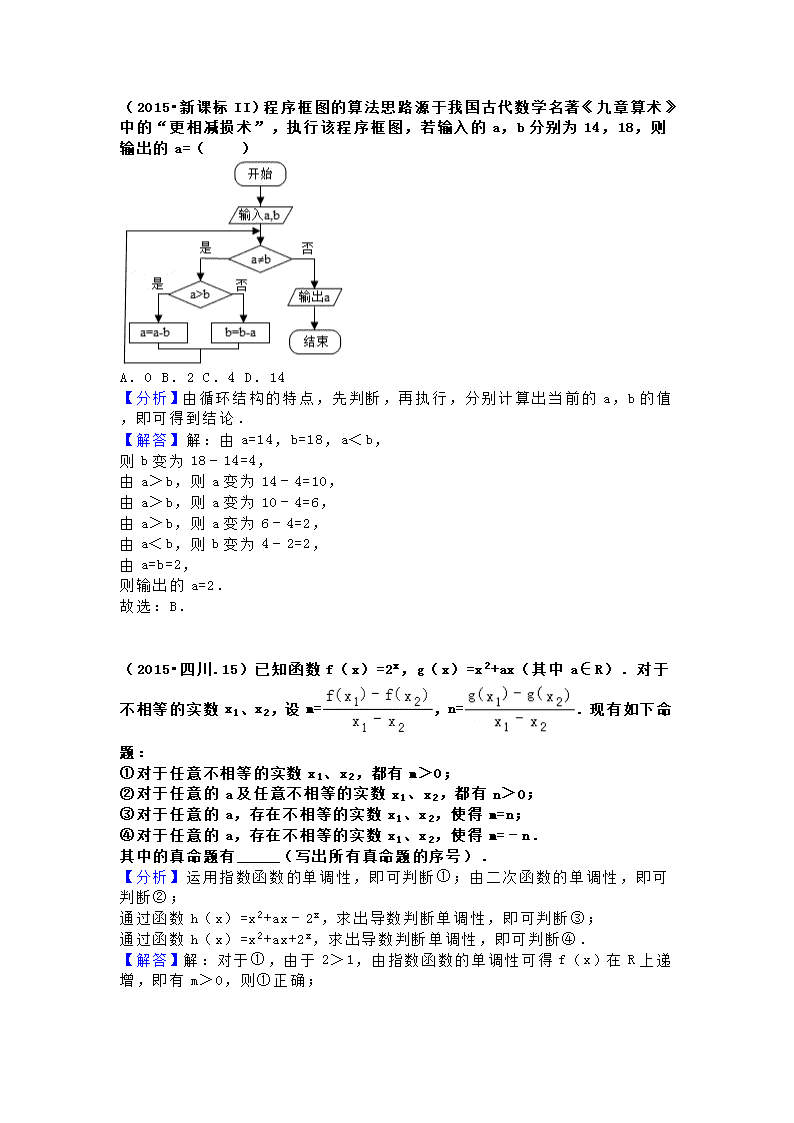
历年四川卷数学高考题部分

‎（2012•四川）如图，动点M到两定点A（﹣1，0）、B（2，0）构成△MAB，且∠MBA=2∠MAB，设动点M的轨迹为C．‎ ‎（Ⅰ）求轨迹C的方程；‎ ‎（Ⅱ）设直线y=﹣2x+m与y轴交于点P，与轨迹C相交于点Q、R，且|PQ|＜|PR|，求的取值范围．‎ ‎【分析】（Ⅰ）设出点M（x，y），分类讨论，根据∠MBA=2∠MAB，利用正切函数公式，建立方程化简即可得到点M的轨迹方程；‎ ‎（Ⅱ）直线y=﹣2x+m与3x2﹣y2﹣3=0（x＞1）联立，消元可得x2﹣4mx+m2+3=0①，利用①有两根且均在（1，+∞）内 可知，m＞1，m≠2设Q，R的坐标，求出xR，xQ，利用，即可确定的取值范围．‎ ‎【解答】解：（Ⅰ）设M的坐标为（x，y），显然有x＞0，且y≠0‎ 当∠MBA=90°时，点M的坐标为（2，±3）‎ 当∠MBA≠90°时，x≠2，由∠MBA=2∠MAB有tan∠MBA=，‎ 化简可得3x2﹣y2﹣3=0‎ 而点（2，±3）在曲线3x2﹣y2﹣3=0上 综上可知，轨迹C的方程为3x2﹣y2﹣3=0（x＞1）；‎ ‎（Ⅱ）直线y=﹣2x+m与3x2﹣y2﹣3=0（x＞1）联立，消元可得x2﹣4mx+m2+3=0①‎ ‎∴①有两根且均在（1，+∞）内 设f（x）=x2﹣4mx+m2+3，∴，∴m＞1，m≠2‎ 设Q，R的坐标分别为（xQ，yQ），（xR，yR），‎ ‎∵|PQ|＜|PR|，∴xR=2m+，xQ=2m﹣，‎ ‎∴==‎ ‎∵m＞1，且m≠2‎ ‎∴，且 ‎∴，且 ‎∴的取值范围是（1，7）∪（7，7+4）‎ ‎（2015•新课标II）设向量，不平行，向量λ+与+2平行，则实数λ=　　．‎ ‎【分析】利用向量平行即共线的条件，得到向量λ+与+2之间的关系，利用向量相等解答．‎ ‎【解答】解：因为向量，不平行，向量λ+与+2平行，所以λ+=μ（+2），‎ 所以，解得；‎ 故答案为：．‎ ‎（2013•四川）已知f（x）是定义域为R的偶函数，当x≥0时，f（x）=x2﹣4x，那么，不等式f（x+2）＜5的解集是　 　．‎ ‎【分析】由偶函数性质得：f（|x+2|）=f（x+2），则f（x+2）＜5可变为f（|x+2|）＜5，代入已知表达式可表示出不等式，先解出|x+2|的范围，再求x范围即可．‎ ‎【解答】解：因为f（x）为偶函数，所以f（|x+2|）=f（x+2），‎ 则f（x+2）＜5可化为f（|x+2|）＜5，‎ 即|x+2|2﹣4|x+2|＜5，（|x+2|+1）（|x+2|﹣5）＜0，‎ 所以|x+2|＜5，‎ 解得﹣7＜x＜3，‎ 所以不等式f（x+2）＜5的解集是（﹣7，3）．‎ 故答案为：（﹣7，3）．‎ ‎（2015•新课标II）程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的a，b分别为14，18，则输出的a=（　　）‎ A．0 B．2 C．4 D．14‎ ‎【分析】由循环结构的特点，先判断，再执行，分别计算出当前的a，b的值，即可得到结论．‎ ‎【解答】解：由a=14，b=18，a＜b，‎ 则b变为18﹣14=4，‎ 由a＞b，则a变为14﹣4=10，‎ 由a＞b，则a变为10﹣4=6，‎ 由a＞b，则a变为6﹣4=2，‎ 由a＜b，则b变为4﹣2=2，‎ 由a=b=2，‎ 则输出的a=2．‎ 故选：B．‎ ‎（2015•四川.15）已知函数f（x）=2x，g（x）=x2+ax（其中a∈R）．对于不相等的实数x1、x2，设m=，n=．现有如下命题：‎ ‎①对于任意不相等的实数x1、x2，都有m＞0；‎ ‎②对于任意的a及任意不相等的实数x1、x2，都有n＞0；‎ ‎③对于任意的a，存在不相等的实数x1、x2，使得m=n；‎ ‎④对于任意的a，存在不相等的实数x1、x2，使得m=﹣n．‎ 其中的真命题有　 　（写出所有真命题的序号）．‎ ‎【分析】运用指数函数的单调性，即可判断①；由二次函数的单调性，即可判断②；‎ 通过函数h（x）=x2+ax﹣2x，求出导数判断单调性，即可判断③；‎ 通过函数h（x）=x2+ax+2x，求出导数判断单调性，即可判断④．‎ ‎【解答】解：对于①，由于2＞1，由指数函数的单调性可得f（x）在R上递增，即有m＞0，则①正确；‎ 对于②，由二次函数的单调性可得g（x）在（﹣∞，﹣）递减，在（﹣，+∞）递增，则n＞0不恒成立，‎ 则②错误；‎ 对于③，由m=n，可得f（x1）﹣f（x2）=g（x1）﹣g（x2），即为g（x1）﹣f（x1）=g（x2）﹣f（x2），‎ 考查函数h（x）=x2+ax﹣2x，h′（x）=2x+a﹣2xln2，‎ 当a→﹣∞，h′（x）小于0，h（x）单调递减，则③错误；‎ 对于④，由m=﹣n，可得f（x1）﹣f（x2）=﹣[g（x1）﹣g（x2）]，考查函数h（x）=x2+ax+2x，‎ h′（x）=2x+a+2xln2，对于任意的a，h′（x）不恒大于0或小于0，则④正确．‎ 故答案为：①④．‎ ‎（2013•四川）已知函数，其中a是实数，设A（x1，f（x1）），B（x2，f（x2））为该函数图象上的点，且x1＜x2．‎ ‎（Ⅰ）指出函数f（x）的单调区间；‎ ‎（Ⅱ）若函数f（x）的图象在点A，B处的切线互相垂直，且x2＜0，求x2﹣x1的最小值；‎ ‎（Ⅲ）若函数f（x）的图象在点A，B处的切线重合，求a的取值范围．‎ ‎【分析】（I）利用二次函数的单调性和对数函数的单调性即可得出；‎ ‎（II）利用导数的几何意义即可得到切线的斜率，因为切线互相垂直，可得，即（2x1+2）（2x2+2）=﹣1．可得，再利用基本不等式的性质即可得出；‎ ‎（III）当x1＜x2＜0或0＜x1＜x2时，∵，故不成立，∴x1＜0＜x2．分别写出切线的方程，根据两条直线重合的充要条件即可得出，再利用导数即可得出．．‎ ‎【解答】解：（I）当x＜0时，f（x）=（x+1）2+a，‎ ‎∴f（x）在（﹣∞，﹣1）上单调递减，在[﹣1，0）上单调递增；‎ 当x＞0时，f（x）=lnx，在（0，+∞）单调递增．‎ ‎（II）∵x1＜x2＜0，∴f（x）=x2+2x+a，∴f′（x）=2x+2，‎ ‎∴函数f（x）在点A，B处的切线的斜率分别为f′（x1），f′（x2），‎ ‎∵函数f（x）的图象在点A，B处的切线互相垂直，‎ ‎∴，‎ ‎∴（2x1+2）（2x2+2）=﹣1．‎ ‎∴2x1+2＜0，2x2+2＞0，‎ ‎∴=1，当且仅当﹣（2x1+2）=2x2+2=1，即，时等号成立．‎ ‎∴函数f（x）的图象在点A，B处的切线互相垂直，且x2＜0，求x2﹣x1的最小值为1．‎ ‎（III）当x1＜x2＜0或0＜x1＜x2时，∵，故不成立，∴x1＜0＜x2．‎ 当x1＜0时，函数f（x）在点A（x1，f（x1）），处的切线方程为 ‎，即．‎ 当x2＞0时，函数f（x）在点B（x2，f（x2））处的切线方程为，即．‎ 函数f（x）的图象在点A，B处的切线重合的充要条件是，‎ 由①及x1＜0＜x2可得﹣1＜x1＜0，‎ 由①②得=．‎ ‎∵函数，y=﹣ln（2x1+2）在区间（﹣1，0）上单调递减，‎ ‎∴a（x1）=在（﹣1，0）上单调递减，且x1→﹣1时，ln（2x1+2）→﹣∞，即﹣ln（2x1+2）→+∞，也即a（x1）→+∞．‎ x1→0，a（x1）→﹣1﹣ln2．‎ ‎∴a的取值范围是（﹣1﹣ln2，+∞）．‎ ‎（2015•新课标II）设函数f′（x）是奇函数f（x）（x∈R）的导函数，f（﹣1）=0，当x＞0时，xf′（x）﹣f（x）＜0，则使得f（x）＞0成立的x的取值范围是（　　）‎ A． ‎（﹣∞，﹣1）∪（0，1） ‎ B． ‎（﹣1，0）∪（1，+∞） ‎ C． ‎（﹣∞，﹣1）∪（﹣1，0） ‎ D． ‎（0，1）∪（1，+∞）‎ ‎【分析】由已知当x＞0时总有xf′（x）﹣f（x）＜0成立，可判断函数g（x）=为减函数，由已知f（x）是定义在R上的奇函数，可证明g（x）为（﹣∞，0）∪（0，+∞）上的偶函数，根据函数g（x）在（0，+∞）上的单调性和奇偶性，模拟g（x）的图象，而不等式f（x）＞0等价于x•g（x）＞0，数形结合解不等式组即可．‎ ‎【解答】解：设g（x）=，则g（x）的导数为：g′（x）=，‎ ‎∵当x＞0时总有xf′（x）＜f（x）成立，‎ 即当x＞0时，g′（x）恒小于0，‎ ‎∴当x＞0时，函数g（x）=为减函数，‎ 又∵g（﹣x）====g（x），‎ ‎∴函数g（x）为定义域上的偶函数 又∵g（﹣1）==0，‎ ‎∴函数g（x）的图象性质类似如图：‎ 数形结合可得，不等式f（x）＞0⇔x•g（x）＞0‎ ‎⇔或，‎ ‎⇔0＜x＜1或x＜﹣1．‎ 故选：A．‎ ‎（2015•新课标II）已知椭圆C：9x2+y2=m2（m＞0），直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．‎ ‎（1）证明：直线OM的斜率与l的斜率的乘积为定值；‎ ‎（2）若l过点（，m），延长线段OM与C交于点P，四边形OAPB能否为平行四边形？若能，求此时l的斜率；若不能，说明理由．‎ ‎【分析】（1）联立直线方程和椭圆方程，求出对应的直线斜率即可得到结论．‎ ‎（2）四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分，即xP=2xM，建立方程关系即可得到结论．‎ ‎【解答】解：（1）设直线l：y=kx+b，（k≠0，b≠0），A（x1，y1），B（x2，y2），M（xM，yM），‎ 将y=kx+b代入9x2+y2=m2（m＞0），得（k2+9）x2+2kbx+b2﹣m2=0，‎ 则判别式△=4k2b2﹣4（k2+9）（b2﹣m2）＞0，‎ 则x1+x2=，则xM==，yM=kxM+b=，‎ 于是直线OM的斜率kOM==，‎ 即kOM•k=﹣9，‎ ‎∴直线OM的斜率与l的斜率的乘积为定值．‎ ‎（2）四边形OAPB能为平行四边形．‎ ‎∵直线l过点（，m），‎ ‎∴由判别式△=4k2b2﹣4（k2+9）（b2﹣m2）＞0，‎ 即k2m2＞9b2﹣9m2，‎ ‎∵b=m﹣m，‎ ‎∴k2m2＞9（m﹣m）2﹣9m2，‎ 即k2＞k2﹣6k，‎ 则k＞0，‎ ‎∴l不过原点且与C有两个交点的充要条件是k＞0，k≠3，‎ 由（1）知OM的方程为y=x，‎ 设P的横坐标为xP，‎ 由得，即xP=，‎ 将点（，m）的坐标代入l的方程得b=，‎ 即l的方程为y=kx+，‎ 将y=x，代入y=kx+，‎ 得kx+=x 解得xM=，‎ 四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分，即xP=2xM，‎ 于是=2×，‎ 解得k1=4﹣或k2=4+，‎ ‎∵ki＞0，ki≠3，i=1，2，‎ ‎∴当l的斜率为4﹣或4+时，四边形OAPB能为平行四边形．‎ ‎（2011•四川）椭圆有两顶点A（﹣1，0）、B（1，0），过其焦点F（0，1）的直线l与椭圆交于C、D两点，并与x轴交于点P．直线AC与直线BD交于点Q．‎ ‎（Ⅰ）当|CD|=时，求直线l的方程；‎ ‎（Ⅱ）当点P异于A、B两点时，求证：为定值．‎ ‎【分析】（Ⅰ）根据椭圆有两顶点A（﹣1，0）、B（1，0），焦点F（0，1），可知椭圆的焦点在y轴上，b=1，c=1，可以求得椭圆的方程，联立直线和椭圆方程，消去y得到关于x的一元二次方程，利用韦达定理和弦长公式可求出直线l的方程；‎ ‎（Ⅱ）根据过其焦点F（0，1）的直线l的方程可求出点P的坐标，该直线与椭圆交于C、D两点，和直线AC与直线BD交于点Q，求出直线AC与直线BD的方程，解该方程组即可求得点Q的坐标，代入即可证明结论．‎ ‎【解答】解：（Ⅰ）∵椭圆的焦点在y轴上，设椭圆的标准方程为（a＞b＞0），‎ 由已知得b=1，c=1，所以a=，‎ 椭圆的方程为，‎ 当直线l与x轴垂直时与题意不符，‎ 设直线l的方程为y=kx+1，C（x1，y1），D（x2，y2），‎ 将直线l的方程代入椭圆的方程化简得（k2+2）x2+2kx﹣1=0，‎ 则x1+x2=﹣，x1•x2=﹣，‎ ‎∴|CD|==‎ ‎==，‎ 解得k=．‎ ‎∴直线l的方程为y=x+1；‎ ‎（Ⅱ）证明：当直线l与x轴垂直时与题意不符，‎ 设直线l的方程为y=kx+1，（k≠0，k≠±1），C（x1，y1），D（x2，y2），‎ ‎∴P点的坐标为（﹣，0），‎ 由（Ⅰ）知x1+x2=﹣，x1•x2=﹣，‎ 且直线AC的方程为y=，且直线BD的方程为y=，‎ 将两直线联立，消去y得，‎ ‎∵﹣1＜x1，x2＜1，∴与异号，‎ ‎=‎ ‎=，‎ y1y2=k2x1x2+k（x1+x2）+1==﹣，‎ ‎∴与y1y2异号，与同号，‎ ‎∴=，解得x=﹣k，‎ 故Q点坐标为（﹣k，y0），‎ ‎=（﹣，0）•（﹣k，y0）=1，‎ 故为定值．‎ ‎（2015•新课标II）设函数f（x）=emx+x2﹣mx．‎ ‎（1）证明：f（x）在（﹣∞，0）单调递减，在（0，+∞）单调递增；‎ ‎（2）若对于任意x1，x2∈[﹣1，1]，都有|f（x1）﹣f（x2）|≤e﹣1，求m的取值范围．‎ ‎【分析】（1）利用f′（x）≥0说明函数为增函数，利用f′（x）≤0说明函数为减函数．注意参数m的讨论；‎ ‎（2）由（1）知，对任意的m，f（x）在[﹣1，0]单调递减，在[0，1]单调递增，则恒成立问题转化为最大值和最小值问题．从而求得m的取值范围．‎ ‎【解答】解：（1）证明：f′（x）=m（emx﹣1）+2x．‎ 若m≥0，则当x∈（﹣∞，0）时，emx﹣1≤0，f′（x）＜0；当x∈（0，+∞）时，emx﹣1≥0，f′（x）＞0．‎ 若m＜0，则当x∈（﹣∞，0）时，emx﹣1＞0，f′（x）＜0；当x∈（0，+∞）时，emx﹣1＜0，f′（x）＞0．‎ 所以，f（x）在（﹣∞，0）时单调递减，在（0，+∞）单调递增．‎ ‎（2）由（1）知，对任意的m，f（x）在[﹣1，0]单调递减，在[0，1]单调递增，故f（x）在x=0处取得最小值．‎ 所以对于任意x1，x2∈[﹣1，1]，|f（x1）﹣f（x2）|≤e﹣1的充要条件是 即 设函数g（t）=et﹣t﹣e+1，则g′（t）=et﹣1．‎ 当t＜0时，g′（t）＜0；当t＞0时，g′（t）＞0．故g（t）在（﹣∞，0）单调递减，在（0，+∞）单调递增．‎ 又g（1）=0，g（﹣1）=e﹣1+2﹣e＜0，故当t∈[﹣1，1]时，g（t）≤0．‎ 当m∈[﹣1，1]时，g（m）≤0，g（﹣m）≤0，即合式成立；‎ 当m＞1时，由g（t）的单调性，g（m）＞0，即em﹣m＞e﹣1．‎ 当m＜﹣1时，g（﹣m）＞0，即e﹣m+m＞e﹣1．‎ 综上，m的取值范围是[﹣1，1]‎ ‎（2015•新课标II）在直角坐标系xOy中，曲线C1：（t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，C3：ρ=2cosθ．‎ ‎（1）求C2与C3交点的直角坐标；‎ ‎（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．‎ ‎【分析】（I）由曲线C2：ρ=2sinθ，化为ρ2=2ρsinθ，把代入可得直角坐标方程．同理由C3：ρ=2cosθ．可得直角坐标方程，联立解出可得C2与C3交点的直角坐标．‎ ‎（2）由曲线C1的参数方程，消去参数t，化为普通方程：y=xtanα，其中0≤α≤π，其极坐标方程为：θ=α（ρ∈R，ρ≠0），利用|AB|=即可得出．‎ ‎【解答】解：（I）由曲线C2：ρ=2sinθ，化为ρ2=2ρsinθ，‎ ‎∴x2+y2=2y．‎ 同理由C3：ρ=2cosθ．可得直角坐标方程：，‎ 联立，‎ 解得，，‎ ‎∴C2与C3交点的直角坐标为（0，0），．‎ ‎（2）曲线C1：（t为参数，t≠0），化为普通方程：y=xtanα，其中0≤α≤π，其极坐标方程为：θ=α（ρ∈R，ρ≠0），‎ ‎∵A，B都在C1上，‎ ‎∴A（2sinα，α），B．‎ ‎∴|AB|==4，‎ 当时，|AB|取得最大值4．‎ ‎（2015•新课标II）若x，y满足约束条件，则z=x+y的最大值为　　．‎ ‎【分析】首先画出平面区域，然后将目标函数变形为直线的斜截式，求在y轴的截距最大值．‎ ‎【解答】解：不等式组表示的平面区域如图阴影部分，当直线经过D点时，z最大，‎ 由得D（1，），‎ 所以z=x+y的最大值为1+；‎ 故答案为：．‎ ‎（2015•新课标II）如图，长方形ABCD的边AB=2，BC=1，O是AB的中点，点P沿着边BC，CD与DA运动，记∠BOP=x．将动点P到A，B两点距离之和表示为x的函数f（x），则y=f（x）的图象大致为（　　）‎ A．B．C．D．‎ ‎【解答】解：当0≤x≤时，BP=tanx，AP==，‎ 此时f（x）=+tanx，0≤x≤，此时单调递增，‎ 当P在CD边上运动时，≤x≤且x≠时，‎ 如图所示，tan∠POB=tan（π﹣∠POQ）=tanx=﹣tan∠POQ=﹣=﹣，‎ ‎∴OQ=﹣，‎ ‎∴PD=AO﹣OQ=1+，PC=BO+OQ=1﹣，‎ ‎∴PA+PB=，‎ 当x=时，PA+PB=2，‎ 当P在AD边上运动时，≤x≤π，PA+PB=﹣tanx，‎ 由对称性可知函数f（x）关于x=对称，‎ 且f（）＞f（），且轨迹为非线型，‎ 排除A，C，D，‎ 故选：B．‎ ‎（2015•新课标II）设Sn是数列{an}的前n项和，且a1=﹣1，an+1=SnSn+1，则Sn=　　．‎ ‎【分析】通过an+1=Sn+1﹣Sn=SnSn+1，并变形可得数列{}是以首项和公差均为﹣1的等差数列，进而可得结论．‎ ‎【解答】解：∵an+1=SnSn+1，‎ ‎∴an+1=Sn+1﹣Sn=SnSn+1，‎ ‎∴=﹣=1，‎ 即﹣=﹣1，‎ 又a1=﹣1，即==﹣1，‎ ‎∴数列{}是以首项和公差均为﹣1的等差数列，‎ ‎∴=﹣1﹣1（n﹣1）=﹣n，‎ ‎∴Sn=﹣，‎ 故答案为：﹣．‎ ‎（2013•四川）节日前夕，小李在家门前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮，那么这两串彩灯同时通电后，它们第一次闪亮的时候相差不超过2秒的概率是（　　）‎ A．B．C．D．‎ ‎【分析】设两串彩灯第一次闪亮的时刻分别为x，y，由题意可得0≤x≤4，0≤y≤4，要满足条件须|x﹣y|≤2，作出其对应的平面区域，由几何概型可得答案．‎ ‎【解答】解：设两串彩灯第一次闪亮的时刻分别为x，y，‎ 由题意可得0≤x≤4，0≤y≤4，‎ 它们第一次闪亮的时候相差不超过2秒，则|x﹣y|≤2，‎ 由几何概型可得所求概率为上述两平面区域的面积之比，‎ 由图可知所求的概率为：=‎ 故选C