中考数学专题复习试卷分类汇编解析版 解直角三角形专题

中考数学专题复习试卷分类汇编解析版 解直角三角形专题

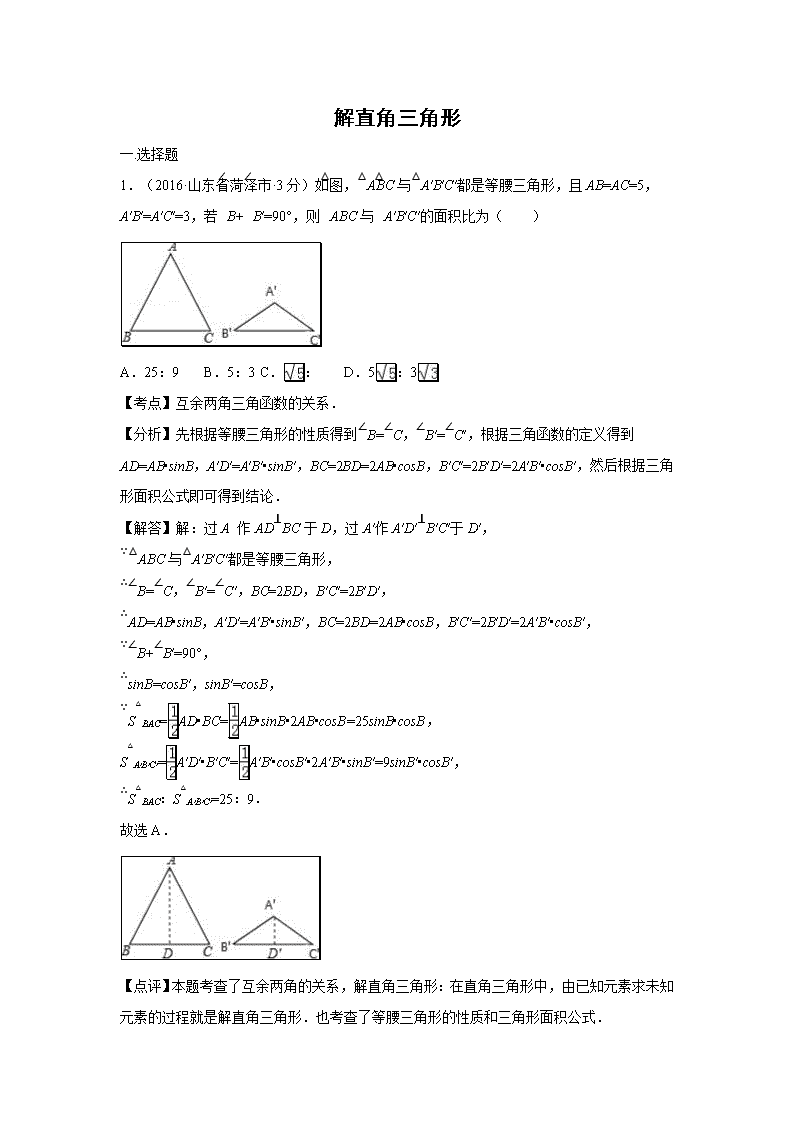
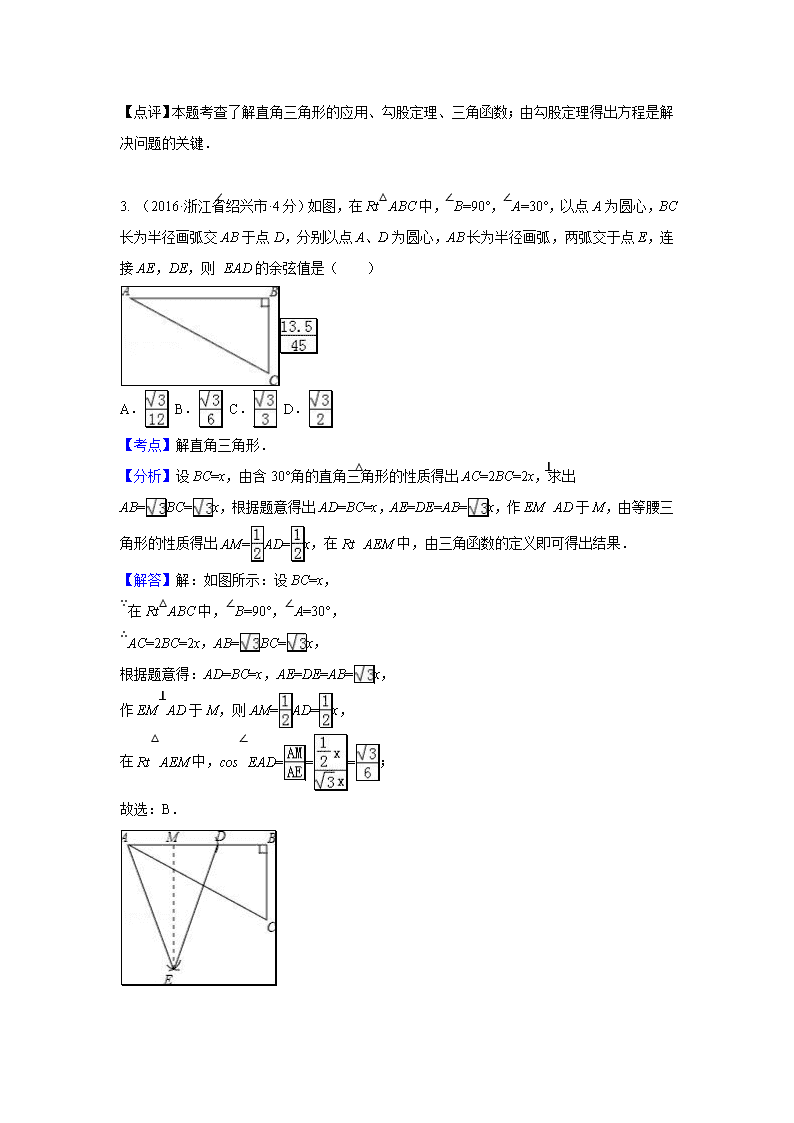
解直角三角形 一.选择题 ‎1．（2016·山东省菏泽市·3分）如图，△ABC与△A′B′C′都是等腰三角形，且AB=AC=5，A′B′=A′C′=3，若∠B+∠B′=90°，则△ABC与△A′B′C′的面积比为（　　）‎ A．25：9 B．5：3 C．： D．5：3‎ ‎【考点】互余两角三角函数的关系．‎ ‎【分析】先根据等腰三角形的性质得到∠B=∠C，∠B′=∠C′，根据三角函数的定义得到AD=AB•sinB，A′D′=A′B′•sinB′，BC=2BD=2AB•cosB，B′C′=2B′D′=2A′B′•cosB′，然后根据三角形面积公式即可得到结论．‎ ‎【解答】解：过A 作AD⊥BC于D，过A′作A′D′⊥B′C′于D′，‎ ‎∵△ABC与△A′B′C′都是等腰三角形，‎ ‎∴∠B=∠C，∠B′=∠C′，BC=2BD，B′C′=2B′D′，‎ ‎∴AD=AB•sinB，A′D′=A′B′•sinB′，BC=2BD=2AB•cosB，B′C′=2B′D′=2A′B′•cosB′，‎ ‎∵∠B+∠B′=90°，‎ ‎∴sinB=cosB′，sinB′=cosB，‎ ‎∵S△BAC=AD•BC=AB•sinB•2AB•cosB=25sinB•cosB，‎ S△A′B′C′=A′D′•B′C′=A′B′•cosB′•2A′B′•sinB′=9sinB′•cosB′，‎ ‎∴S△BAC：S△A′B′C′=25：9．‎ 故选A．‎ ‎【点评】本题考查了互余两角的关系，解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了等腰三角形的性质和三角形面积公式．‎ ‎2. （2016·重庆市A卷·4分）某数学兴趣小组同学进行测量大树CD高度的综合实践活动，如图，在点A处测得直立于地面的大树顶端C的仰角为36°，然后沿在同一剖面的斜坡AB行走‎13米至坡顶B处，然后再沿水平方向行走‎6米至大树脚底点D处，斜面AB的坡度（或坡比）i=1：2.4，那么大树CD的高度约为（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73）（　　） ‎ ‎ ‎ A．8.1米 B．17.2米 C．19.7米 D．25.5米 ‎【分析】作BF⊥AE于F，则FE=BD=‎6米，DE=BF，设BF=x米，则AF=‎2.4米，在Rt△ABF中，由勾股定理得出方程，解方程求出DE=BF=‎5米，AF=‎12米，得出AE的长度，在Rt△ACE中，由三角函数求出CE，即可得出结果． ‎ ‎【解答】解：作BF⊥AE于F，如图所示： ‎ 则FE=BD=‎6米，DE=BF， ‎ ‎∵斜面AB的坡度i=1：2.4， ‎ ‎∴AF=2.4BF， ‎ 设BF=x米，则AF=2.4x米， ‎ 在Rt△ABF中，由勾股定理得：x2+（2.4x）2=132， ‎ 解得：x=5， ‎ ‎∴DE=BF=‎5米，AF=‎12米， ‎ ‎∴AE=AF+FE=‎18米， ‎ 在Rt△ACE中，CE=AEtan36°=18×0.73=‎13.14米， ‎ ‎∴CD=CE﹣DE=‎13.14米﹣‎5米≈‎8.1米； ‎ 故选：A． ‎ ‎ ‎ ‎【点评】本题考查了解直角三角形的应用、勾股定理、三角函数；由勾股定理得出方程是解决问题的关键． ‎ ‎3. （2016·浙江省绍兴市·4分）如图，在Rt△ABC中，∠B=90°，∠A=30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（　　）‎ A． B． C． D．‎ ‎【考点】解直角三角形．‎ ‎【分析】设BC=x，由含30°角的直角三角形的性质得出AC=2BC=2x，求出AB=BC=x，根据题意得出AD=BC=x，AE=DE=AB=x，作EM⊥AD于M，由等腰三角形的性质得出AM=AD=x，在Rt△AEM中，由三角函数的定义即可得出结果．‎ ‎【解答】解：如图所示：设BC=x，‎ ‎∵在Rt△ABC中，∠B=90°，∠A=30°，‎ ‎∴AC=2BC=2x，AB=BC=x，‎ 根据题意得：AD=BC=x，AE=DE=AB=x，‎ 作EM⊥AD于M，则AM=AD=x，‎ 在Rt△AEM中，cos∠EAD===；‎ 故选：B．‎ ‎4. （2016·重庆市B卷·4分）如图所示，某办公大楼正前方有一根高度是‎15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是‎20米，梯坎坡长BC是‎12米，梯坎坡度i=1：，则大楼AB的高度约为（　　）（精确到‎0.1米，参考数据：≈1.41，≈1.73，≈2.45）‎ A．30.6 B．32.1 C．37.9 D．39.4‎ ‎【考点】解直角三角形的应用-坡度坡角问题．‎ ‎【分析】延长AB交DC于H，作EG⊥AB于G，则GH=DE=‎15米，EG=DH，设BH=x米，则CH=x米，在Rt△BCH中，BC=‎12米，由勾股定理得出方程，解方程求出BH=‎6米，CH=‎6米，得出BG、EG的长度，证明△AEG是等腰直角三角形，得出AG=EG=6+20（米），即可得出大楼AB的高度．‎ ‎【解答】解：延长AB交DC于H，作EG⊥AB于G，如图所示：‎ 则GH=DE=‎15米，EG=DH，‎ ‎∵梯坎坡度i=1：，‎ ‎∴BH：CH=1：，‎ 设BH=x米，则CH=x米，‎ 在Rt△BCH中，BC=‎12米，‎ 由勾股定理得：x2+（x）2=122，‎ 解得：x=6，∴BH=‎6米，CH=6米，‎ ‎∴BG=GH﹣BH=15﹣6=9（米），EG=DH=CH+CD=6+20（米），‎ ‎∵∠α=45°，‎ ‎∴∠EAG=90°﹣45°=45°，‎ ‎∴△AEG是等腰直角三角形，‎ ‎∴AG=EG=6+20（米），‎ ‎∴AB=AG+BG=6+20+9≈39.4（米）；‎ 故选：D．‎ ‎【点评】本题考查了解直角三角形的应用﹣坡度、俯角问题；通过作辅助线运用勾股定理求出BH，得出EG是解决问题的关键．‎ 二.填空题 ‎1．（2016·山东省菏泽市·3分）如图，在正方形ABCD外作等腰直角△CDE，DE=CE，连接BE，则tan∠EBC=　　．‎ ‎【考点】正方形的性质；等腰直角三角形；解直角三角形．‎ ‎【专题】计算题．‎ ‎【分析】作EF⊥BC于F，如图，设DE=CE=a，根据等腰直角三角形的性质得CD=CE=a，∠DCE=45°，再利用正方形的性质得CB=CD=a，∠BCD=90°，接着判断△CEF为等腰直角三角形得到CF=EF=CE=a，然后在Rt△BEF中根据正切的定义求解．‎ ‎【解答】解：作EF⊥BC于F，如图，设DE=CE=a，‎ ‎∵△CDE为等腰直角三角形，‎ ‎∴CD=CE=a，∠DCE=45°，‎ ‎∵四边形ABCD为正方形，‎ ‎∴CB=CD=a，∠BCD=90°，‎ ‎∴∠ECF=45°，‎ ‎∴△CEF为等腰直角三角形，‎ ‎∴CF=EF=CE=a，‎ 在Rt△BEF中，tan∠EBF===，‎ 即∠EBC=．‎ 故答案为．‎ ‎【点评】本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有四边形、平行四边形、矩形、菱形的一切性质．也考查了等腰直角三角形的性质．‎ ‎2. （2016·湖北荆州·3分）全球最大的关公塑像矗立在荆州古城东门外．如图，张三同学在东门城墙上C处测得塑像底部B处的俯角为18°48′，测得塑像顶部A处的仰角为45°，点D在观测点C正下方城墙底的地面上，若CD=‎10米，则此塑像的高AB约为　‎58　‎米（参考数据：tan78°12′≈4.8）．‎ ‎【分析】直接利用锐角三角函数关系得出EC的长，进而得出AE的长，进而得出答案．‎ ‎【解答】解：如图所示：由题意可得： CE⊥AB于点E，BE=DC，‎ ‎∵∠ECB=18°48′，‎ ‎∴∠EBC=78°12′，‎ 则tan78°12′===4.8，‎ 解得：EC=48（m），‎ ‎∵∠AEC=45°，则AE=EC，且BE=DC=10m，‎ ‎∴此塑像的高AB约为：AE+EB=58（米）．‎ 故答案为：58．‎ ‎【点评】此题主要考查了解直角三角形的应用，根据题意得出EC的长是解题关键．‎ 三.解答题 ‎1. （2016·湖北随州·8分）某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度，已知烈山坡面与水平面的夹角为30°，山高857.5尺，组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点，在点E处测得雕像顶端A的仰角为60°，求雕像AB的高度．‎ ‎【考点】解直角三角形的应用-仰角俯角问题．‎ ‎【分析】构造直角三角形，利用锐角三角函数，进行简单计算即可．‎ ‎【解答】解：如图，‎ 过点E作EF⊥AC，EG⊥CD，‎ 在Rt△DEG中，∵DE=1620，∠D=30°，‎ ‎∴EG=DEsin∠D=1620×=810，‎ ‎∵BC=857.5，CF=EG，‎ ‎∴BF=BC﹣CF=47.5，‎ 在Rt△BEF中，tan∠BEF=，‎ ‎∴EF=BF，‎ 在Rt△AEF中，∠AEF=60°，设AB=x，‎ ‎∵tan∠AEF=，‎ ‎∴AF=EF×tan∠AEF，‎ ‎∴x+47.5=3×47.5，‎ ‎∴x=95，‎ 答：雕像AB的高度为95尺．‎ ‎2. （2016·吉林·7分）如图，某飞机于空中A处探测到目标C，此时飞行高度AC=1200m，从飞机上看地平面指挥台B的俯角α=43°，求飞机A与指挥台B的距离（结果取整数）‎ ‎（参考数据：sin43°=0.68，cos43°=0.73，tan43°=0.93）‎ ‎【考点】解直角三角形的应用-仰角俯角问题．‎ ‎【分析】先利用平行线的性质得到∠B=α=43°，然后利用∠B的正弦计算AB的长．‎ ‎【解答】解：如图，∠B=α=43°，‎ 在Rt△ABC中，∵sinB=，‎ ‎∴AB=≈1765（m）．‎ 答：飞机A与指挥台B的距离为1765m．‎ ‎3. （2016·江西·8分）如图1是一副创意卡通圆规，图2是其平面示意图，OA是支撑臂，OB是旋转臂，使用时，以点A为支撑点，铅笔芯端点B可绕点A旋转作出圆．已知OA=OB=10cm．‎ ‎（1）当∠AOB=18°时，求所作圆的半径；（结果精确到0.01cm）‎ ‎（2）保持∠AOB=18°不变，在旋转臂OB末端的铅笔芯折断了一截的情况下，作出的圆与（1）中所作圆的大小相等，求铅笔芯折断部分的长度．（结果精确到0.01cm）‎ ‎（参考数据：sin9°≈0.1564，cos9°≈0.9877，sin18°≈0.3090，cos18°≈0.9511，可使用科学计算器）‎ ‎【考点】解直角三角形的应用．‎ ‎【分析】（1）根据题意作辅助线OC⊥AB于点C，根据OA=OB=10cm，∠OCB=90°，∠AOB=18°，可以求得∠BOC的度数，从而可以求得AB的长；‎ ‎（2）由题意可知，作出的圆与（1）中所作圆的大小相等，则AE=AB，然后作出相应的辅助线，画出图形，从而可以求得BE的长，本题得以解决．‎ ‎【解答】解：（1）作OC⊥AB于点C，如右图2所示，‎ 由题意可得，OA=OB=10cm，∠OCB=90°，∠AOB=18°，‎ ‎∴∠BOC=9°‎ ‎∴AB=2BC=2OB•sin9°≈2×10×0.1564≈3.13cm，‎ 即所作圆的半径约为3.13cm；‎ ‎（2）作AD⊥OB于点D，作AE=AB，如下图3所示，‎ ‎∵保持∠AOB=18°不变，在旋转臂OB末端的铅笔芯折断了一截的情况下，作出的圆与（1）中所作圆的大小相等，‎ ‎∴折断的部分为BE，‎ ‎∵∠AOB=18°，OA=OB，∠ODA=90°，‎ ‎∴∠OAB=81°，∠OAD=72°，‎ ‎∴∠BAD=9°，‎ ‎∴BE=2BD=2AB•sin9°≈2×3.13×0.1564≈0.98cm，‎ 即铅笔芯折断部分的长度是0.98cm．‎ ‎　‎ ‎4. （2016·辽宁丹东·10分）某中学九年级数学兴趣小组想测量建筑物AB的高度．他们在C处仰望建筑物顶端，测得仰角为48°，再往建筑物的方向前进‎6米到达D处，测得仰角为64°，求建筑物的高度．（测角器的高度忽略不计，结果精确到‎0.1米）‎ ‎（参考数据：sin48°≈，tan48°≈，sin64°≈，tan64°≈2）‎ ‎【考点】解直角三角形的应用-仰角俯角问题．‎ ‎【分析】Rt△ADB中用AB表示出BD、Rt△ACB中用AB表示出BC，根据CD=BC﹣BD可得关于AB 的方程，解方程可得．‎ ‎【解答】解：根据题意，得∠ADB=64°，∠ACB=48°‎ 在Rt△ADB中，tan64°=，‎ 则BD=≈AB，‎ 在Rt△ACB中，tan48°=，‎ 则CB=≈AB，‎ ‎∴CD=BC﹣BD 即6=AB﹣AB 解得：AB=≈14.7（米），‎ ‎∴建筑物的高度约为‎14.7米．‎ ‎5. （2016·四川宜宾）如图，CD是一高为‎4米的平台，AB是与CD底部相平的一棵树，在平台顶C点测得树顶A点的仰角α=30°，从平台底部向树的方向水平前进‎3米到达点E，在点E处测得树顶A点的仰角β=60°，求树高AB（结果保留根号）‎ ‎【考点】解直角三角形的应用-仰角俯角问题．‎ ‎【分析】作CF⊥AB于点F，设AF=x米，在直角△ACF中利用三角函数用x表示出CF的长，在直角△ABE中表示出BE的长，然后根据CF﹣BE=DE即可列方程求得x的值，进而求得AB的长．‎ ‎【解答】解：作CF⊥AB于点F，设AF=x米，‎ 在Rt△ACF中，tan∠ACF=，‎ 则CF====x，‎ 在直角△ABE中，AB=x+BF=4+x（米），‎ 在直角△ABF中，tan∠AEB=，则BE===（x+4）米．‎ ‎∵CF﹣BE=DE，即x﹣（x+4）=3．‎ 解得：x=，‎ 则AB=+4=（米）．‎ 答：树高AB是米．‎ ‎6.（2016·湖北黄石·8分）如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=‎800米，BC=‎200米，坡角∠BAF=30°，∠CBE=45°．‎ ‎（1）求AB段山坡的高度EF；‎ ‎（2）求山峰的高度CF．（1.414，CF结果精确到米）‎ ‎【分析】（1）作BH⊥AF于H，如图，在Rt△ABF中根据正弦的定义可计算出BH的长，从而得到EF的长；‎ ‎（2）先在Rt△CBE中利用∠CBE的正弦计算出CE，然后计算CE和EF的和即可．‎ ‎【解答】解：（1）作BH⊥AF于H，如图，‎ 在Rt△ABF中，∵sin∠BAH=，‎ ‎∴BH=800•sin30°=400，‎ ‎∴EF=BH=400m；‎ ‎（2）在Rt△CBE中，∵sin∠CBE=，‎ ‎∴CE=200•sin45°=100≈141.4，‎ ‎∴CF=CE+EF=141.4+400≈541（m）．‎ 答：AB段山坡高度为‎400米，山CF的高度约为‎541米．‎ ‎【点评】本题考查了解直角三角形的应用﹣坡度与坡角问题：坡度是坡面的铅直高度h和水平宽度l的比，又叫做坡比，它是一个比值，反映了斜坡的陡峭程度，一般用i表示，常写成i=1：m的形式．把坡面与水平面的夹角α叫做坡角，坡度i与坡角α之间的关系为：i═tanα．‎ ‎7．（2016·湖北荆门·6分）如图，天星山山脚下西端A处与东端B处相距800（1+）米，小军和小明同时分别从A处和B处向山顶C 匀速行走．已知山的西端的坡角是45°，东端的坡角是30°，小军的行走速度为米/秒．若小明与小军同时到达山顶C处，则小明的行走速度是多少？‎ ‎【考点】解直角三角形的应用-坡度坡角问题．‎ ‎【分析】过点C作CD⊥AB于点D，设AD=x米，小明的行走速度是a米/秒，根据直角三角形的性质用x表示出AC与BC的长，再根据小明与小军同时到达山顶C处即可得出结论．‎ ‎【解答】解：过点C作CD⊥AB于点D，设AD=x米，小明的行走速度是a米/秒，‎ ‎∵∠A=45°，CD⊥AB，‎ ‎∴AD=CD=x米，‎ ‎∴AC=x．‎ 在Rt△BCD中，‎ ‎∵∠B=30°，‎ ‎∴BC===2x，‎ ‎∵小军的行走速度为米/秒．若小明与小军同时到达山顶C处，‎ ‎∴=，解得a=‎1米/秒．‎ 答：小明的行走速度是‎1米/秒．‎ ‎　‎ ‎8.（2016·四川内江）(9分)如图8，禁渔期间，我渔政船在A处发现正北方向B处有一艘可疑船只，测得A，B两处距离为200海里，可疑船只正沿南偏东45°方向航行．我渔政船迅速沿北偏东30°方向前去拦截，经历4小时刚好在C 处将可疑船只拦截．求该可疑船只航行的平均速度(结果保留根号)．‎ 北 C A B ‎30°‎ ‎45°‎ 图8‎ 北 C A B ‎30°‎ ‎45°‎ 答案图 H ‎[考点]三角函数、解决实际问题。‎ 解：如图，过点C作CH⊥AB于H，则△BCH是等腰直角三角形．设CH＝x，‎ 则BH＝x，AH＝CH÷30°＝x． 2分 ‎∵AB＝200，∴x＋x＝200．‎ ‎∴x＝＝100(－1)． 4分 ‎∴BC＝x＝100(－)． 6分 ‎∵两船行驶4小时相遇，‎ ‎∴可疑船只航行的平均速度＝100(－)÷4＝45(－)． 8分 答：可疑船只航行的平均速度是每小时45(－)海里． 9分 ‎9．（2016·四川泸州）如图，为了测量出楼房AC的高度，从距离楼底C处60米的点D（点D与楼底C在同一水平面上）出发，沿斜面坡度为i=1：的斜坡DB前进‎30米到达点B，在点B处测得楼顶A的仰角为53°，求楼房AC的高度（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈，计算结果用根号表示，不取近似值）．‎ ‎【考点】解直角三角形的应用-仰角俯角问题；解直角三角形的应用-坡度坡角问题．‎ ‎【分析】如图作BN⊥CD于N，BM⊥AC于M，先在RT△BDN中求出线段BN，在RT△ABM中求出AM，再证明四边形CMBN是矩形，得CM=BN即可解决问题．‎ ‎【解答】解：如图作BN⊥CD于N，BM⊥AC于M．‎ 在RT△BDN中，BD=30，BN：ND=1：，‎ ‎∴BN=15，DN=15，‎ ‎∵∠C=∠CMB=∠CNB=90°，‎ ‎∴四边形CMBN是矩形，‎ ‎∴CM=BM=15，BM=CN=60﹣15=45，‎ 在RT△ABM中，tan∠ABM==，‎ ‎∴AM=27，‎ ‎∴AC=AM+CM=15+27．‎ ‎10. （2016·云南省昆明市）如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据：≈1.414，≈1.732）‎ ‎【考点】解直角三角形的应用-仰角俯角问题．‎ ‎【分析】如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．通过解直角△AFD得到DF的长度；通过解直角△DCE得到CE的长度，则BC=BE﹣CE．‎ ‎【解答】解：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．‎ 则DE=BF=CH=10m，‎ 在直角△ADF中，∵AF=80m﹣10m=70m，∠ADF=45°，‎ ‎∴DF=AF=70m．‎ 在直角△CDE中，∵DE=10m，∠DCE=30°，‎ ‎∴CE===10（m），‎ ‎∴BC=BE﹣CE=70﹣10≈70﹣17.32≈52.7（m）．‎ 答：障碍物B，C两点间的距离约为52.7m．‎ ‎11. （2016·浙江省绍兴市·8分）如图1，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走60m到达C点，测得点B在点C的北偏东60°方向，如图2．‎ ‎（1）求∠CBA的度数．‎ ‎（2）求出这段河的宽（结果精确到1m，备用数据≈1.41，≈1.73）．‎ ‎【考点】解直角三角形的应用-方向角问题．‎ ‎【分析】（1）根据三角形的外角的性质、结合题意计算即可；‎ ‎（2）作BD⊥CA交CA的延长线于D，设BD=xm，根据正切的定义用x表示出CD、AD，根据题意列出方程，解方程即可．‎ ‎【解答】解：（1）由题意得，∠BAD=45°，∠BCA=30°，‎ ‎∴∠CBA=∠BAD﹣∠BCA=15°；‎ ‎（2）作BD⊥CA交CA的延长线于D，‎ 设BD=xm，‎ ‎∵∠BCA=30°，‎ ‎∴CD==x，‎ ‎∵∠BAD=45°，‎ ‎∴AD=BD=x，‎ 则x﹣x=60，‎ 解得x=≈82，‎ 答：这段河的宽约为82m．‎ ‎12．（2016海南）如图，在大楼AB的正前方有一斜坡CD，CD=‎4米，坡角∠DCE=30°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上．‎ ‎（1）求斜坡CD的高度DE；‎ ‎（2）求大楼AB的高度（结果保留根号）‎ ‎【考点】解直角三角形的应用-仰角俯角问题；解直角三角形的应用-坡度坡角问题．‎ ‎【专题】应用题；解直角三角形及其应用．‎ ‎【分析】（1）在直角三角形DCE中，利用锐角三角函数定义求出DE的长即可；‎ ‎（2）过D作DF垂直于AB，交AB于点F，可得出三角形BDF为等腰直角三角形，设BF=DF=x，表示出BC，BD，DC，由题意得到三角形BCD为直角三角形，利用勾股定理列出关于x的方程，求出方程的解得到x的值，即可确定出AB的长．‎ ‎【解答】解：（1）在Rt△DCE中，DC=‎4米，∠DCE=30°，∠DEC=90°，‎ ‎∴DE=DC=‎2米；‎ ‎（2）过D作DF⊥AB，交AB于点F，‎ ‎∵∠BFD=90°，∠BDF=45°，‎ ‎∴∠BFD=45°，即△BFD为等腰直角三角形，‎ 设BF=DF=x米，‎ ‎∵四边形DEAF为矩形，‎ ‎∴AF=DE=‎2米，即AB=（x+2）米，‎ 在Rt△ABC中，∠ABC=30°，‎ ‎∴BC====米，‎ BD=BF=x米，DC=‎4米，‎ ‎∵∠DCE=30°，∠ACB=60°，‎ ‎∴∠DCB=90°，‎ 在Rt△BCD中，根据勾股定理得：2x2=+16，‎ 解得：x=4+或x=4﹣，‎ 则AB=（6+）米或（6﹣）米．‎ ‎【点评】此题考查了解直角三角形﹣仰角俯角问题，坡度坡角问题，熟练掌握勾股定理是解本题的关键．‎ ‎13．（2016河南）如图，小东在教学楼距地面‎9米高的窗口C处，测得正前方旗杆顶部A点的仰角为37°，旗杆底部B点的俯角为45°，升旗时，国旗上端悬挂在距地面‎2.25米处，若国旗随国歌声冉冉升起，并在国歌播放45秒结束时到达旗杆顶端，则国旗应以多少米/秒的速度匀速上升？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）‎ ‎【考点】解直角三角形的应用-仰角俯角问题．‎ ‎【分析】通过解直角△BCD和直角△ACD分别求得BD、CD以及AD的长度，则易得AB的长度，则根据题意得到整个过程中旗子上升高度，由“速度=”进行解答即可．‎ ‎【解答】解：在Rt△BCD中，BD=‎9米，∠BCD=45°，则BD=CD=‎9米．‎ 在Rt△ACD中，CD=‎9米，∠ACD=37°，则AD=CD•tan37°≈9×0.75=6.75（米）．‎ 所以，AB=AD+BD=‎15.75米，‎ 整个过程中旗子上升高度是：15.75﹣2.25=13.5（米），‎ 因为耗时45s，‎ 所以上升速度v==0.3（米/秒）．‎ 答：国旗应以‎0.3米/秒的速度匀速上升．‎ ‎【点评】本题考查了解直角三角形的应用﹣仰角俯角问题．解决此类问题要了解角之间的关系，找到与已知和未知相关联的直角三角形，当图形中没有直角三角形时，要通过作高或垂线构造直角三角形，另当问题以一个实际问题的形式给出时，要善于读懂题意，把实际问题划归为直角三角形中边角关系问题加以解决．‎ ‎14.（2016·山东省菏泽市·3分）南沙群岛是我国固有领土，现在我南海渔民要在南沙某海岛附近进行捕鱼作业，当渔船航行至B处时，测得该岛位于正北方向20（1+）海里的C处，为了防止某国还巡警干扰，就请求我A处的鱼监船前往C处护航，已知C位于A处的北偏东45°方向上，A位于B的北偏西30°的方向上，求A、C之间的距离．‎ ‎【考点】解直角三角形的应用-方向角问题．‎ ‎【分析】作AD⊥BC，垂足为D，设CD=x，利用解直角三角形的知识，可得出AD，继而可得出BD，结合题意BC=CD+BD可得出方程，解出x的值后即可得出答案．‎ ‎【解答】解：如图，作AD⊥BC，垂足为D，‎ 由题意得，∠ACD=45°，∠ABD=30°．‎ 设CD=x，在Rt△ACD中，可得AD=x，‎ 在Rt△ABD中，可得BD=x，‎ 又∵BC=20（1+），CD+BD=BC，‎ 即x+x=20（1+），‎ 解得：x=20，‎ ‎∴AC=x=20（海里）．‎ 答：A、C之间的距离为20海里．‎ ‎【点评】此题考查了解直角三角形的应用，解答本题的关键是根据题意构造直角三角形，将实际问题转化为数学模型进行求解，难度一般．‎ ‎15．（2016·山东省德州市·4分）‎2016年2月1日，我国在西昌卫星发射中心，用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道，如图，火箭从地面L处发射，当火箭达到A点时，从位于地面R处雷达站测得AR的距离是6km，仰角为42.4°；1秒后火箭到达B点，此时测得仰角为45.5°‎ ‎（1）求发射台与雷达站之间的距离LR；‎ ‎（2）求这枚火箭从A到B的平均速度是多少（结果精确到0.01）？‎ ‎（参考数据：son42.4°≈0.67，cos42.4°≈0.74，tan42.4°≈0.905，sin45.5°≈0.71，cos45.5°≈0.70，tan45.5°≈1.02 ）‎ ‎【考点】勾股定理的应用．‎ ‎【分析】（1）根据题意直接利用锐角三角函数关系得出LR=AR•cos∠ARL求出答案即可；‎ ‎（2）根据题意直接利用锐角三角函数关系得出BL=LR•tan∠BRL，再利用AL=ARsin∠ARL，求出AB的值，进而得出答案．‎ ‎【解答】解：（1）在Rt△ALR中，AR=6km，∠ARL=42.4°，‎ 由cos∠ARL=，得LR=AR•cos∠ARL=6×cos42.4°≈4.44（km）．‎ 答：发射台与雷达站之间的距离LR为4.44km；‎ ‎（2）在Rt△BLR中，LR=4.44km，∠BRL=45.5°，‎ 由tan∠BRL=，得BL=LR•tan∠BRL=4.44×tan45.5°≈4.44×1.02=4.5288（km），‎ 又∵sin∠ARL=，得AL=ARsin∠ARL=6×sin42.4°≈4.02（km），‎ ‎∴AB=BL﹣AL=4.5288﹣4.02=0.5088≈0.51（km）．‎ 答：这枚火箭从A到B的平均速度大约是0.51km/s．‎ ‎【点评】此题主要考查了解直角三角形的应用，正确选择锐角三角函数关系是解题关键．‎ ‎16．（2016·山东省济宁市·3分）某地的一座人行天桥如图所示，天桥高为‎6米，坡面BC的坡度为1：1，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为1：．‎ ‎（1）求新坡面的坡角a；‎ ‎（2）原天桥底部正前方‎8米处（PB的长）的文化墙PM是否需要拆桥？请说明理由．‎ ‎【考点】解直角三角形的应用-坡度坡角问题．‎ ‎【分析】（1）由新坡面的坡度为1：，可得tanα=tan∠CAB==，然后由特殊角的三角函数值，求得答案；‎ ‎（2）首先过点C作CD⊥AB于点D，由坡面BC的坡度为1：1，新坡面的坡度为1：．即可求得AD，BD的长，继而求得AB的长，则可求得答案．‎ ‎【解答】解：（1）∵新坡面的坡度为1：，‎ ‎∴tanα=tan∠CAB==，‎ ‎∴∠α=30°．‎ 答：新坡面的坡角a为30°；‎ ‎（2）文化墙PM不需要拆除．‎ 过点C作CD⊥AB于点D，则CD=6，‎ ‎∵坡面BC的坡度为1：1，新坡面的坡度为1：，‎ ‎∴BD=CD=6，AD=6，‎ ‎∴AB=AD﹣BD=6﹣6＜8，‎ ‎∴文化墙PM不需要拆除．‎