张家界市2011年中考数学试卷

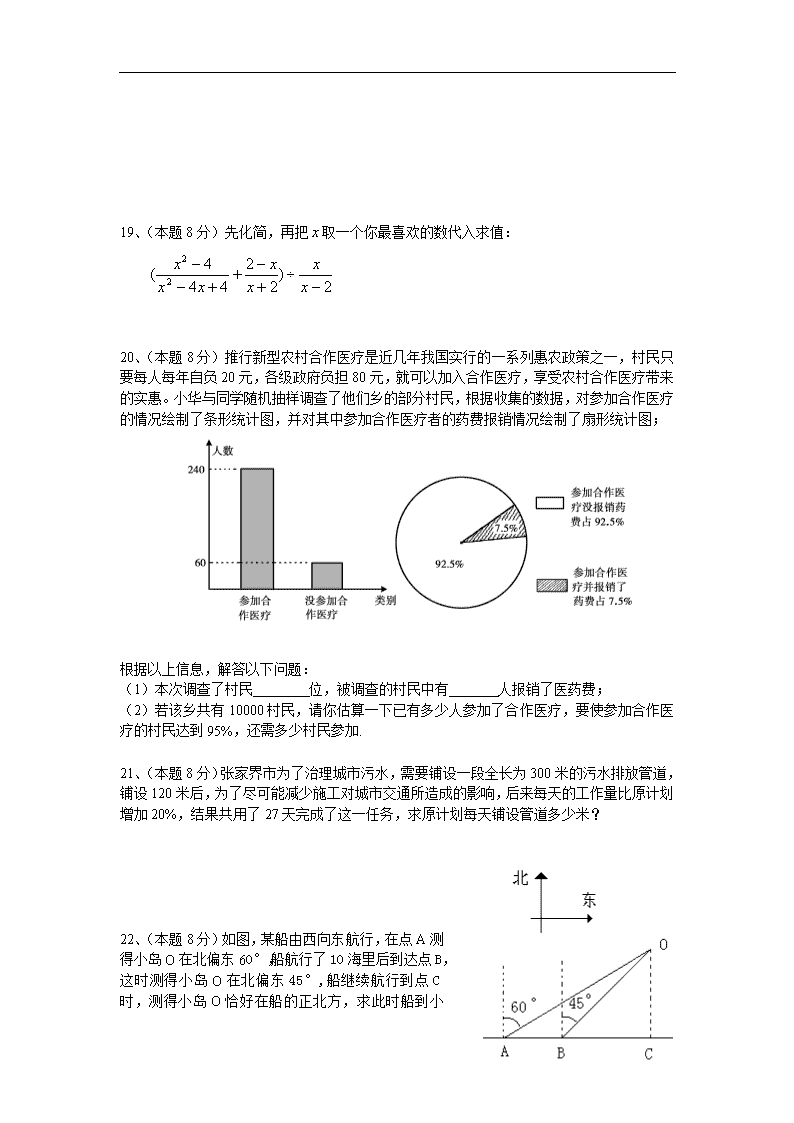
张家界市2011年中考数学试卷

张家界市2011年初中毕业学业考试试卷 数 学 考生注意：本卷共三道大题，25个小题，满分120分，考试时量120分钟 一、选择题（本大题共8个小题，每小题3分，满分24分）‎ ‎1、计算 ：的结果是（ ）‎ A、 1 B、 —‎1 C、 2011 D、 —2011‎ ‎2、下列事件中，不是必然事件的是（）‎ A、对顶角相等 B、内错角相等 ‎ C、三角形内角和等于180° D、 等腰梯形是轴对称图形 ‎3、一家鞋店对上一周某品牌女鞋的销量统计如下：‎ 尺码（厘米）‎ ‎22‎ ‎22.5‎ ‎23‎ ‎23.5‎ ‎24‎ ‎24.5‎ ‎25‎ 销量（双）‎ ‎1‎ ‎2‎ ‎5‎ ‎11‎ ‎7‎ ‎3‎ ‎1‎ 该店决定本周进货时，多进一些尺码为23.5厘米的鞋，影响鞋店决策的统计量是（ ）‎ A、 平均数 B、中位数 C、方差 D、众数 ‎4、不等式的解集是（ ）‎ A、 B、 C、 D、 ‎ ‎5、已知1是关于的一元二次方程的一个根，则的值是（ ）‎ ‎ A、1 B、—‎1 C、0 D、无法确定 ‎6、顺次连接任意一个四边形四边的中点所得到的四边形一定是（ ）‎ A、平行四边形 B、矩形 C菱形 D正方形 ‎7、已知两圆相外切，连心线长度是10厘米，其中一圆的半径为6厘米，则另一圆的半径是（ ）‎ A、16厘米 B、10厘米 C、6厘米 D、4厘米 ‎8、关于的一次函数的图像可能是（ ）‎ ‎ ‎ 二、填空题（本大题共8个小题，每小题3分，满分24分）‎ ‎9、‎2011年4月10日4时47分，我国第八颗北斗导航卫星发射成功，标志着北斗区域卫星导航系统的基本系统建成，打破了欧美对该领域的垄断。据中科院详细估算，该系统到2020年有望形成价值400000000000元的产业，用科学计数法表示为 元。‎ ‎10、我们可以利用计数器求一个正数的平方根，其操作方法是按顺序进行按键输入： ‎ ‎ .小明按键输入 显示结果为4，则他按键 输入显示结果应为 .‎ ‎11、因式分解 .‎ ‎12、如图是一个几何体的三视图，则这个几何体的名称是 .‎ ‎13、如图，点P是反比例函数图像上的一点，则矩形PEOF的面积是 . ‎ ‎14、两个袋子中分别装着写有1、2、3、4的四张卡片，从每一个袋子中各抽取一张，则两张卡片上的数字之和是6的机会是 .‎ ‎15、如图，在△ABC中，AB=AC，点D为BC边的中点，‎ ‎∠BAD=20°，则∠C= .‎ ‎16、在△ABC中， AB=8，AC=6，在△DEF中，DE＝４,DF=3，要使△ABC与△DEF相似，则需添加的一个条件是 （写出一种情况即可）.‎ 三、解答题（本大题共9个小题，满分为72分）‎ ‎17、（本题6分）计算：‎ ‎18、（本题6分）将16个相同的小正方形拼成正方形网格，并将其中的两个小正方形涂成黑色，请你用两种不同的方法分别在图甲、图乙中再将两个空白的小正方形涂黑，使它成为轴对称图形.‎ ‎19、（本题8分）先化简，再把取一个你最喜欢的数代入求值：‎ ‎20、（本题8分）推行新型农村合作医疗是近几年我国实行的一系列惠农政策之一，村民只要每人每年自负20元，各级政府负担80元，就可以加入合作医疗，享受农村合作医疗带来的实惠。小华与同学随机抽样调查了他们乡的部分村民，根据收集的数据，对参加合作医疗的情况绘制了条形统计图，并对其中参加合作医疗者的药费报销情况绘制了扇形统计图；‎ 根据以上信息，解答以下问题：‎ ‎（1）本次调查了村民 位，被调查的村民中有 人报销了医药费；‎ ‎（2）若该乡共有10000村民，请你估算一下已有多少人参加了合作医疗，要使参加合作医疗的村民达到95%，还需多少村民参加.‎ ‎21、（本题8分）张家界市为了治理城市污水，需要铺设一段全长为‎300米的污水排放管道，铺设‎120米后，为了尽可能减少施工对城市交通所造成的影响，后来每天的工作量比原计划增加20%，结果共用了27天完成了这一任务，求原计划每天铺设管道多少米？‎ ‎22、（本题8分）如图，某船由西向东航行，在点A测得小岛O在北偏东60°，船航行了10海里后到达点B，这时测得小岛O在北偏东45°,船继续航行到点C时，测得小岛O 恰好在船的正北方，求此时船到小岛的距离.‎ ‎23、（本题8分）阅读材料：‎ 如果是一元二次方程的两根，那么，，‎ ‎。这就是著名的韦达定理。现在我们利用韦达定理解决问题：‎ 已知是方程的两根 ‎（1）填空： ， ；‎ ‎（2）计算的值。‎ ‎24、（本题8分）如图，在⊙Ｏ中，直径ＡＢ的两侧有定点Ｃ和动点Ｐ，点Ｐ在弧ＡＢ上运动（不与A、B重合），过点C作ＣＰ的垂线，与ＰＢ的延长线交于点Ｑ.‎ ‎（１）试猜想：△ＰＣＱ与△ＡＣＢ具有何种关系？（不要求证明）；‎ ‎（２）当点Ｐ运动到什么位置时，△ABC≌△PCB ,并给出证明.‎ ‎25、（本题12分）如图，抛物线经过点A（—4，0）、B（—2，2），连接OB、AB，‎ ‎（1）求该抛物线的解析式.‎ ‎（2）求证：△OAB是等腰直角三角形.‎ ‎（3）将△OAB绕点O按逆时针方向旋转135°，得到△OA′B′，写出A′B′的中点P的坐标，试判断点P是否在此抛物线上.‎ ‎（4）在抛物线上是否存在这样的点M，使得四边形ABOM成直角梯形，若存在，请求出点M坐标及该直角梯形的面积，若不存在，请说明理由.‎ 参考答案 一、选择题（每题3分，共计24分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 A B D C B A D C 一、 填空题（每题3分，共计24分）‎ ‎9、 10、圆锥 11、‎ ‎12、40 13、 6 14 ‎ ‎15、 70° 16、∠A= ∠D （或者BC:EF = 2:1）‎ 三、解答题（8个小题，共计60分）‎ ‎17、解：原式= 1—2 + 1‎ ‎ =0…………………………6分 ‎18、注意：方法很多，每做对一种给4分，共计8分 ‎19、解：原式 = ‎ ‎ =‎ ‎ =‎ ‎=‎ ‎=……………………………………6分 代值计算……………………………………8分 注意：可取除0、2、—2以外的任何实数。‎ ‎20、（1）300 18 （2）8000 1500 （注意：每数2分，共8分）‎ ‎21、解：设原计划每天铺设管道米…………………2分 则…………………………4分 解得（米）………………………………6分 经检验，是原方程的解。‎ 答：原计划每天铺设管道10米。………………8分 ‎22、解：设OC=海里，依题意得 ‎ BC=OC=, AC =………………….3 分 ‎ ∴AC-BC=10‎ ‎ （）‎ ‎ ……………………………..6分 ‎ 答：船与小岛的距离是海里。……………………8分 ‎23、（1） 3 (每空2分共4分)‎ ‎(2) …………………..6分 ‎ =2……………………….8分 ‎24、（1）△PCQ～△ACB…………………………3分 ‎（2）当PC过圆心时，△ABC△PCB…..4分 证明：∵PC和AB都是⊙O的直径 ‎ ∴∠ACB=∠PBC=90°……………………5分 ‎ 且AB=PC………………………………6分 ‎ 又∠A=∠P…………………………….7分 ‎ ∴△ABC≌△PCB……………………..8分 ‎25、解：（1）由A（—4，0）、B（—2，2）在抛物线图像上，得：‎ ‎ …………………2分 解之得：‎ ‎ ‎ ‎∴ 该函数解析式为：y= ……….4分 ‎ ‎ （2）过点B作BC垂直于X轴，垂足是点C. ……………………6分 ‎ 易知：线段CO、CA、CB的长度均为2‎ ‎ ∴ △ABC和△OBC为全等的等腰直角三角形 ‎　　　　∴　ＡＢ＝ＯＢ ‎ 且∠ABO=∠ＡＢＣ＋∠ＯＢＣ＝　‎ ‎　　　　∴　△OAB是等腰直角三角形　　　　．．．．．．．．．．．．．．．．．．．．８分 （３） 如图，将△OAB绕点O按逆时针方向旋转135°，得到△OA′B′‎ 其中点B′正好落在轴上且B′A′∥轴．‎ 又∵ＯB′和A′B′的长度为 A′B′中点P的坐标为，显然不满足抛物线方程，‎ ‎∴　点P不在此抛物线上．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１０分 ‎　　（４）　存在　　．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１１分 ‎　　　　　　　过点O，作OM∥AB交抛物线于点M　‎ ‎　　　　　　易求出直线OM的解析式为：‎ ‎ 联立抛物线解析式得： 解之得 ‎ 点M（—6，—6） ‎ ‎ 显然，点M（—6，—6）关于对称轴的对称点M′（2,—6）也满足要求，‎ ‎ 故满足条件的点M共有两个，坐标分别为（—6，—6）和（2，—6）‎ ‎ ∴=×4×2+×4×6=16 ………….12分 ‎ （注：此题方法较多，只要合理均可给分）‎