中考数学复习猜想求证型问题

中考数学复习猜想求证型问题

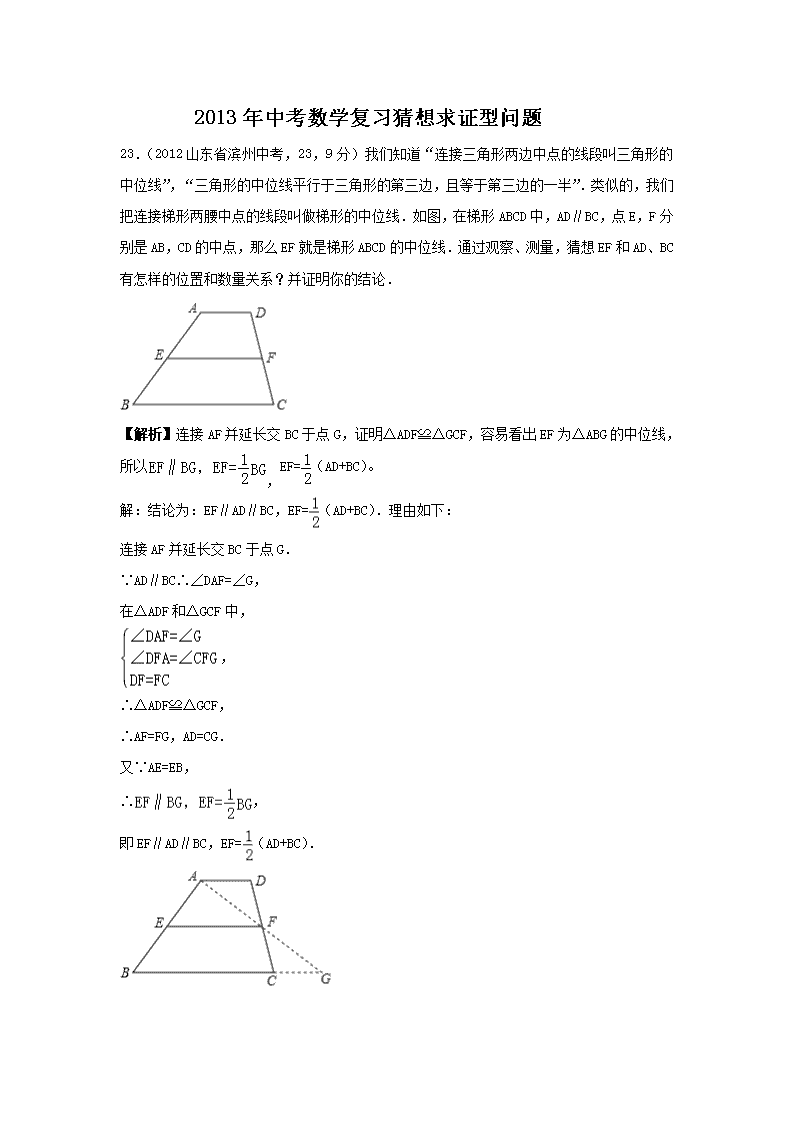
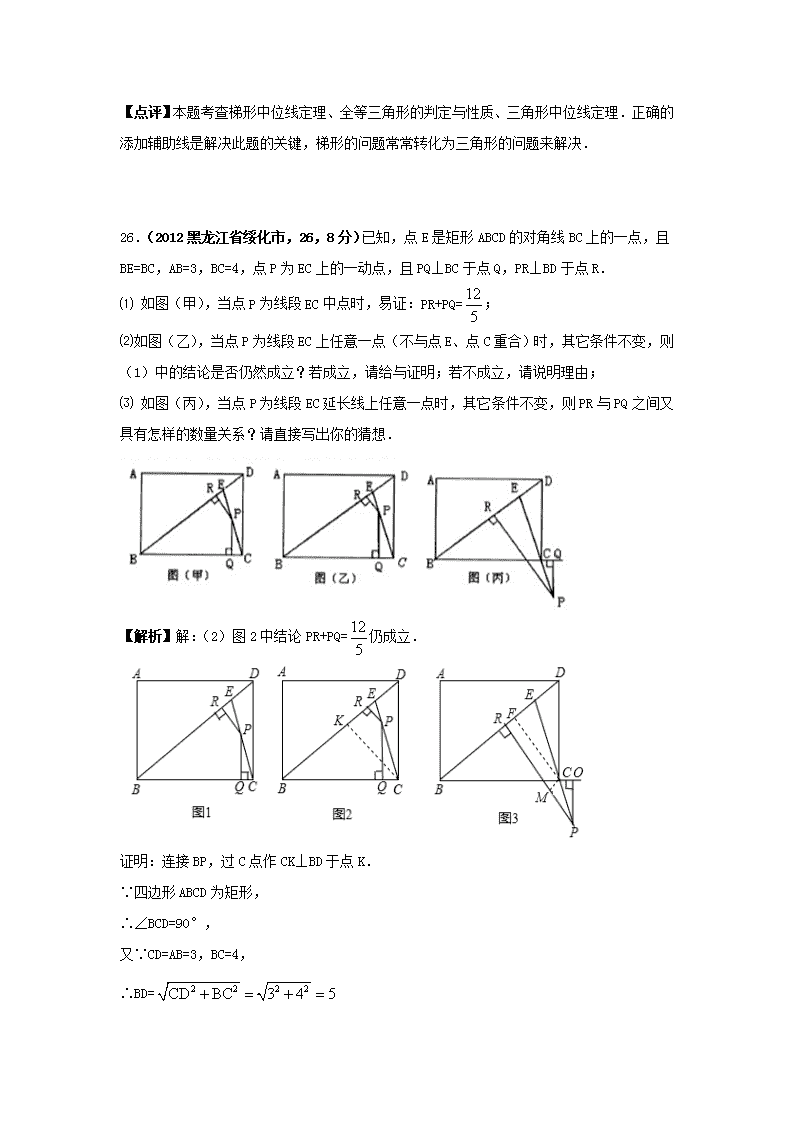
‎2013年中考数学复习猜想求证型问题 ‎23．（2012山东省滨州中考，23，9分）我们知道“连接三角形两边中点的线段叫三角形的中位线”，“三角形的中位线平行于三角形的第三边，且等于第三边的一半”．类似的，我们把连接梯形两腰中点的线段叫做梯形的中位线．如图，在梯形ABCD中，AD∥BC，点E，F分别是AB，CD的中点，那么EF就是梯形ABCD的中位线．通过观察、测量，猜想EF和AD、BC有怎样的位置和数量关系？并证明你的结论．‎ ‎【解析】连接AF并延长交BC于点G，证明△ADF≌△GCF，容易看出EF为△ABG的中位线，所以，EF=（AD+BC）。‎ 解：结论为：EF∥AD∥BC，EF=（AD+BC）．理由如下：‎ 连接AF并延长交BC于点G．‎ ‎∵AD∥BC∴∠DAF=∠G，‎ 在△ADF和△GCF中，‎ ‎，‎ ‎∴△ADF≌△GCF，‎ ‎∴AF=FG，AD=CG．‎ 又∵AE=EB，‎ ‎∴，‎ 即EF∥AD∥BC，EF=（AD+BC）．‎ ‎【点评】本题考查梯形中位线定理、全等三角形的判定与性质、三角形中位线定理．正确的添加辅助线是解决此题的关键，梯形的问题常常转化为三角形的问题来解决．‎ ‎26．（2012黑龙江省绥化市，26，8分）已知，点E是矩形ABCD的对角线BC上的一点，且BE=BC，AB=3，BC=4，点P为EC上的一动点，且PQ⊥BC于点Q，PR⊥BD于点R．‎ ‎⑴ 如图（甲），当点P为线段EC中点时，易证：PR+PQ=；‎ ‎⑵ 如图（乙），当点P为线段EC上任意一点（不与点E、点C重合）时，其它条件不变，则（1）中的结论是否仍然成立？若成立，请给与证明；若不成立，请说明理由；‎ ‎⑶ 如图（丙），当点P为线段EC延长线上任意一点时，其它条件不变，则PR与PQ之间又具有怎样的数量关系？请直接写出你的猜想．‎ ‎【解析】解：（2）图2中结论PR+PQ=仍成立．‎ ‎ 证明：连接BP，过C点作CK⊥BD于点K．‎ ‎∵四边形ABCD为矩形， ∴∠BCD=90°， 又∵CD=AB=3，BC=4， ∴BD=‎ ‎∵S△BCD=BC•CD=BD•CK，‎ 即3×4=5CK， ∴CK=‎ ‎∵S△BCE=BE•CK，S△BEP=PR•BE，S△BCP= PQ•BC，且S△BCE=S△BEP+S△BCP，‎ ‎∴BE•CK=PR•BE+PQ•BC 又∵BE=BC，‎ ‎∴CK=PR+PQ，∴PR+PQ=‎ ‎（3）图3中的结论是PR-PQ=．‎ ‎【答案】⑵结论PR+PQ=仍然成立，理由见解析；⑶图（丙）中的结论是PR-PQ=．‎ ‎【点评】本题主要考查了矩形的性质及直角三角形的重要定理：勾股定理，解决本题的关键是掌握好矩形的性质及以图形面积的和差为平台构造出的等式关系．难度中等．‎ ‎23. （2012山东省青岛市，23，10）（10分）问题提出：以n边形的n个顶点和它内部的m个点，共（m+n）个点为顶点，可把原n边形分割成多少个互不重叠的小三角形？‎ 问题探究：为了解决上面的问题，我们将采取一般问题特殊化的策略，先从简单和具体的情形入手：‎ 探究一：以△ABC的三个顶点和它内部的一个点P，共4个点为顶点，可把△ABC分割成多少个互不重叠的小三角形？‎ 如图①，显然，此时可把△ABC分割成3个互不重叠的小三角形.‎ 探究二：以△ABC的三个顶点和它内部的2个点P、Q，共5个点为顶点，可把△ABC分割成多少个互不重叠的小三角形？‎ 在探究一的基础上，我们可看作在图①△ABC的内部，再添加1个点Q，那么点Q的位置会有两种情况：‎ 一种情况，点Q在图①分割成的某个小三角形内部，不妨假设点Q在△PAC内部，如图②；‎ 另一种情况，点Q在图①分割成的小三角形的某条公共边上，不妨假设点Q在PA上，如图③；‎ 显然，不管哪种情况，都可把△ABC分割成5个互不重叠的小三角形.‎ 探究三：以△ABC的三个顶点和它内部的3个点P、Q、R，共6个点为顶点可把△ABC分割成 个互不重叠的小三角形，并在图④画出一种分割示意图.‎ 探究四：以△ABC的三个顶点和它内部的m个点，共（m+3）个顶点可把△ABC分割成 ‎ ‎ 个互不重叠的小三角形。‎ 探究拓展：以四边形的4个顶点和它内部的m个点，共（m+4）个顶点，可把四边形分割成 个互不重叠的小三角形。‎ 问题解决：以n边形的n个顶点和它内部的m个点，共（m+n）个顶点，可把△ABC分割成 个互不重叠的小三角形。‎ 实际应用：以八边形的8个顶点和它内部的2012个点，共2020个点，可把八边形分割成多少个互不重叠的小三角形？（要求列式计算）‎ ‎23. 【解析】观察图形发现：内部每多一个点，则多2个三角形，从而得到一般规律为n+2(m-1)或‎2m+n-2.根据根据规律逐一解答.‎ ‎【答案】探究三：7‎ 分割示意图.（答案不唯一）.‎ 探究四：3+2（m-1）或‎2m+1 ‎ 探究拓展：4+2（m-1）或‎2m+2‎ 问题解决：n+2(m-1)或‎2m+n-2‎ 实际应用：把n=8,m=2012代入上述代数式，得‎2m+n-2=2×2012+8-2=4024+8-2=4030.‎ ‎【点评】本题考查规律型中的图形变化问题，解题关键是结合图形，探寻其规律，发现规律才能顺利解题，体现特殊到一般的数学思想．‎ ‎16．（2012贵州遵义，16,4分）猜数字游戏中，小明写出如下一组数：，，，，…，小亮猜想出第六个数字是，根据此规律，第n个数是　　．‎ 解析：‎ 根据分数的分子是2n，分母是2n+3，进而得出答案即可．‎ 解：∵分数的分子分别是：2 2=4，23=8，24=16，…‎ 分数的分母分别是：2 2+3=7，23+3=11，24+3=19，…‎ ‎∴第n个数是．‎ 故答案为：．‎ 答案：‎ 点评：‎ 此题主要考查了数字变化规律，根据已知得出分子与分母的变化规律是解题关键．‎ ‎26. （2012年吉林省，第26题、10分．）‎ 问题情境 如图，在x轴上有两点A（m,0）,B(n, 0)(n＞m＞0).分别过点A，点B作x轴的垂线，交抛物线y=x²于点C，点D.直线OC交直线BD于点E，直线OD交直线AC于点F,点E,点F的纵坐标分别记为,.‎ 特例探究 填空：‎ 当m=1,n=2时，=____,=______.‎ 当m=3,n=5时，=_____,=______.‎ 归纳证明 对任意m, n（n>m>0）,猜想与的大小关系，并证明你的猜想 拓展应用.‎ 1. 若将“抛物线y=x²”改为“抛物线y=ax²（a>0）”,其它条件不变，请直接写出与的大小关系.‎ 2. 连接EF， AE．当时，直接写出m和n的关系及四边形OFEA的形状．‎ ‎【解析】【特例探究】【归纳证明】都是【拓展应用】（1）的特殊情况，因此以【拓展】（1）为例说明前三小问的思路：已知A、B的坐标，根据抛物线的解析式，能得到C、D的坐标，进而能求出直线OC、OD的解析式，也就能得出E、F两点的坐标，再进行比较即可．最后一小题也比较简单：总结前面的结论，能得出EF∥x轴的结论，那么直角梯形OFEB的面积和△OFE的面积比例关系，能判断出EF、OA的比例关系，进而得出m、n的关系，再对四边形OFEA的形状进行判定．‎ ‎【答案】‎ 解：特例探究 当m=1，n=2时，A（1，0）、B（2，0）、C（1，1）、D（2，4）；‎ 则：直线OC的解析式为：y=x；直线OD解析式为：y=2x；‎ ‎∴F（1，2）、E（2，2）；‎ 即．‎ 同理：当m=3，n=5时，． 归纳证明 猜想：‎ 证明：‎ 则，C， D OD的解析式为y=nx OC的解析式为y=mx E在OC上，横坐标为n，‎ 当x=n时，‎ F在OD上，横坐标为m 当x=m时，‎ ‎∴‎ 拓展应用 （1） 设 则 OD的解析式为 当x=n时，；当x=m时．‎ ‎∴‎ ‎(2)∵四边形OFEB是直角梯形，EF=n-m,OB=n, BE=mn 又 ‎∴‎ 可得， EF=m, OA=m ‎∴EF‖OA且EF=OA.‎ ‎∴四边形OFEA是平行四边形．‎ ‎【点评】本题主要考查的是一次函数解析式的确定和二次函数的性质、图形面积的解法、平行四边形的判定等知识，综合性较强，本题由特殊到一般、由浅入深的引导方式进一步降低了题目的难度，对于基础知识的掌握是解题的关键．‎ ‎28．（2012黑龙江省绥化市，28，10分）如图，四边形ABCD为矩形，C点在x轴上，A点在y轴上，D点的坐标是（0，0），B点的坐标是（3，4），矩形ABCD沿直线EF折叠，点A落在BC边上的G处，E、F分别在AD和AB上，且F点的坐标是（2，4）．‎ ‎⑴ 求G点坐标；‎ ‎⑵ 求直线EF的解析式；‎ ‎⑶ 点N在x轴上，直线EF上是否存在点M，使以M、N、F、G为顶点的四边形是平行四边形．若存在，请直接写出M点坐标；若不存在，请说明理由．‎ ‎【解析】解：⑴由已知得，FG=AF=2，FB=1‎ ‎∵四边形ABCD为矩形 ‎∴∠B=900‎ ‎∴BG=‎ ‎∴点G坐标为（3，4 -）‎ ‎⑵设：直线EF的解析式是 ‎∵在Rt△BFG中，cos∠BFG== ‎∴∠BFG=600，∴∠AFE=∠EFG=600‎ ‎∴AE=AFtan∠AFE=2tan600=2 ‎∴E点的坐标是（0，）‎ 又∵F点的坐标是（2,4）‎ ‎∴解得 ‎∴直线EF的解析式是；‎ ‎⑶．存在：‎ ‎、、．‎ ‎【答案】 ⑴G点坐标（3，）；‎ ‎⑵；‎ ‎⑶、、．‎ ‎【点评】 本题综合考查了矩形的性质、勾股定理、待定系数法求直线解析式、三角函数及特殊角的三角函数值、平行四边形的性质等多个知识点．‎ 还考查了考生数形结合思想、分类讨论思想等多个常见的初中数学思想．对考生在知识、方法及能力方面均有较高的要求．难度较大．‎ ‎21．（2012四川省资阳市，21，8分）已知、是正实数，那么，是恒成立的．‎ ‎（1）(3分)由恒成立，说明恒成立；‎ ‎（2）(3分)填空：已知、、是正实数，由恒成立，‎ 猜测： 也恒成立；‎ ‎（3）(2分)如图，已知AB是直径，点P是弧上异于点A和点B的一点，PC⊥AB，垂足为C，AC＝，ＢC＝，由此图说明恒成立．‎ ‎（第21题图）‎ ‎【解析】（1）由完全平方的非负性及完全平方公式展开再运用不等式性质1即可证得.‎ ‎（2）由（1）得出：“两正实数的平均数不小于这两正实数积的算术平方根”，挖掘规律得出答案.‎ ‎（3）由“点到直线上所有点的连线段中垂线段最短”的性质及相似构造出不等式的形式.‎ ‎【答案】‎ ‎（1）由得，………1分 于是 ………………………………2分 ‎∴……………………………………3分 ‎（2）……………………………………6分 ‎（3）连结OP，‎ ‎∵AB是直径，∴∠APB=90°，又∵PC⊥AB，∴Rt△APC∽Rt△PBC，∴，，……………………………………………………………7分 又∵，由垂线段最短，得，∴…………………………8分 ‎【点评】本题主要是将高中不等式知识通过初中的知识去理解证明，主要考查了考生观察、类比、归纳的能力.解决此种题型的关键是灵活运用初数的各个知识点及了解初高中数学知识的衔接.难度较大.‎ ‎（2012浙江省衢州，19，6分）如图，在□ABCD中，E、F是对角线BD上的两点，且BE=DF，连接AE、CF.请你猜想：AE与CF有怎样的数量关系？并对你的猜想加以证明.‎ ‎【解析】AE与CF有怎样的数量关系，可从AE与CF所在的△ABE和△CDF是否全等来考虑，先由平行四边形的性质得出AB=CD，∠ABE=∠CDF，再加上已知BE=DF，可推出△ABE≌△CDF，得证．‎ ‎【答案】猜想：AE＝CF ‎∵四边形ABCD是平行四边形，‎ ‎ ∴AB∥CD，AB＝CD …2分 ‎ ∴∠ABE＝∠CDF …3分 ‎ 又∵BE=DF ‎ ∴△ABE≌△CDF …5分 ‎ ‎∴AE＝CF …6分 ‎【点评】此题考查的知识点是平行四边形的性质与全等三角形的判定和性质，关键是证明AF与CF所在的三角形全等．全等三角形的判定，常见的判断方法有5种 ‎，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．‎ ‎24．（2012湖南湘潭，24，8分）如图，是边长为的等边三角形，将沿直线向右平移,使点与点重合，得到，连结，交于.‎ ‎（1）猜想与的位置关系，并证明你的结论；‎ ‎（2）求线段的长.‎ ‎【解析】用平行四边形和菱形的判断方法和性质进行推理，‎ 将沿直线向右平移,CD∥AB，且CD=AB，‎ 则四边形ABCD是平行四边形，又有AB=BC，则四边形ABCD是菱形，‎ 菱形的对角线互相垂直平分。‎ ‎（2）用勾股定理或三角函数求出等边三角形的高BF=，由菱形的性质得BD=2BF=。‎ ‎【答案】（1）猜想与的位置关系是互相垂直平分，证明如:下：‎ 因是等边三角形，则AB=BC=AC=3，将沿直线向右平移后,CD∥AB，且CD=AB，则四边形ABCD是平行四边形，又有AB=BC，则四边形ABCD是菱形，菱形ABCD的对角线与互相垂直平分。‎ ‎（2）BC=3，CF=，∠BFC=900，BF==，由菱形的性质得BD=2BF=。‎ ‎【点评】本题主要考查菱形和平行四边形的性质和判断方法，对角线互相垂直平分，是菱形的性质。[来 ‎17. （2012安徽，17，8分）在由m×n（m×n＞1）个小正方形组成的矩形网格中，研究它的一条对角线所穿过的小正方形个数f，‎ ‎（1）当m、n互质（m、n除1外无其他公因数）时，观察下列图形并完成下表：‎ ‎1‎ ‎2‎ ‎3‎ ‎2‎ ‎1‎ ‎3‎ ‎4‎ ‎3‎ ‎2‎ ‎3‎ ‎5‎ ‎4‎ ‎2‎ ‎4‎ ‎7‎ ‎3‎ ‎5‎ ‎7‎ ‎ ‎ 猜想：当m、n互质时，在m×n的矩形网格中，一条对角线所穿过的小正方形的个数f与m、n的关系式是______________________________（不需要证明）；‎ 解：‎ ‎（2）当m、n不互质时，请画图验证你猜想的关系式是否依然成立，‎ ‎17：解析：（1）通过题中所给网格图形，先计算出2×5，3×4，对角线所穿过的小正方形个数f，再对照表中数值归纳f与m、n的关系式.‎ ‎（2）根据题意，画出当m、n不互质时，结论不成立的反例即可.‎ 解：（1）如表：‎ ‎1‎ ‎2‎ ‎3‎ ‎2‎ ‎1‎ ‎3‎ ‎4‎ ‎3‎ ‎2‎ ‎3‎ ‎5‎ ‎4‎ ‎2‎ ‎4‎ ‎7‎ ‎6‎ ‎3‎ ‎5‎ ‎7‎ ‎6‎ f=m+n-1‎ ‎（2）当m、n不互质时，上述结论不成立，如图2×4‎ ‎2×4‎ 点评：本题是操作探究题，根据操作规则得出数据，并归纳总结其中规律，对于错误结论的证明，只要举出反例即可.‎