2020年山东省济南市历下区中考数学三模试卷

2020年山东省济南市历下区中考数学三模试卷

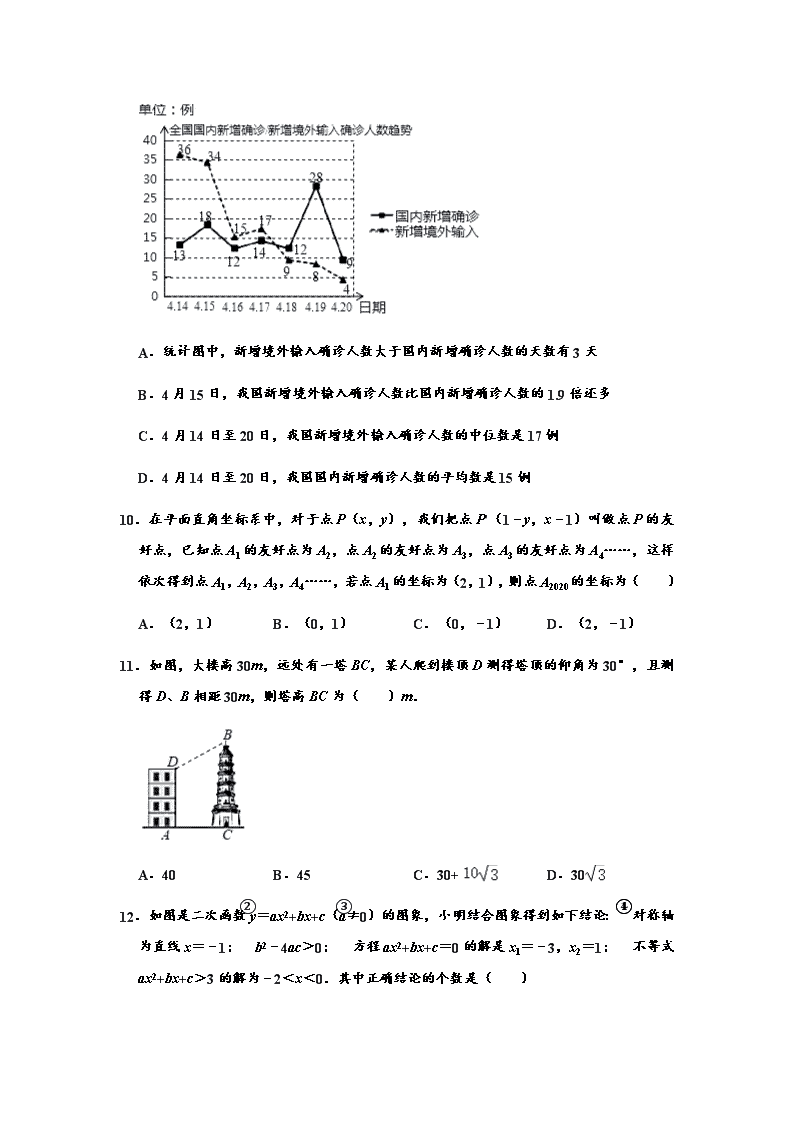
‎2020年山东省济南市历下区中考数学三模试卷（B卷）‎ 一、选择题 ‎1．64的平方根是（　　）‎ A．±8 B．±4 C．8 D．32‎ ‎2．如图，一个几何体由5个大小相同的正方体搭成，则这个立体图形的俯视图是（　　）‎ A． B． ‎ C． D．‎ ‎3．中国人民解放军海军山东舰是中国首艘自主建造的国产航母，该舰的满载排水量为67500吨，数字67500用科学记数法表示为（　　）‎ A．67.5×104 B．6.75×104 C．0.675×105 D．6.75×105‎ ‎4．如图，DE∥CF，∠1＝45°，∠2＝30°，则∠BDF等于（　　）‎ A．15° B．25° C．30° D．35°‎ ‎5．若m＞n，则下列不等式正确的是（　　）‎ A．m+2＜n+2 B．m﹣2＜n﹣2 C．﹣2m＜﹣2n D．m2＞n2‎ ‎6．窗棂即窗格（窗里面的横的或竖的格）是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种花纹，构成种类繁多的优美图案，下列表示我国古代窗棂样式结构图案中既是轴对称图形又是中心对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎7．若点A（x1，1）、B（x2，﹣2）、C（x3，﹣3）在反比例函数y＝﹣的图象上，则x1、x2、x3的大小关系是（　　）‎ A．x1＜x2＜x3 B．x1＜x3＜x2 C．x3＜x1＜x2 D．x2＜x1＜x3‎ ‎8．如图，在平面直角坐标系xOy中，△ABC与△A1B1C1是中心对称图形．则对称中心的坐标是（　　）‎ A．（1，1） B．（1，0） C．（1，﹣1） D．（1，﹣2）‎ ‎9．如图，统计图反映了我国2020年4月14日至20日新型冠状病毒肺炎全国国内新增确诊和新增境外输入确诊人数趋势，根据统计图提供的信息，下列推断合理的是（　　）‎ A．统计图中，新增境外输入确诊人数大于国内新增确诊人数的天数有3天 ‎ B．4月15日，我国新增境外输入确诊人数比国内新增确诊人数的1.9倍还多 ‎ C．4月14日至20日，我国新增境外输入确诊人数的中位数是17例 ‎ D．4月14日至20日，我国国内新增确诊人数的平均数是15例 ‎10．在平面直角坐标系中，对于点P（x，y），我们把点P'（1﹣y，x﹣1）叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4……，这样依次得到点A1，A2，A3，A4……，若点A1的坐标为（2，1），则点A2020的坐标为（　　）‎ A．（2，1） B．（0，1） C．（0，﹣1） D．（2，﹣1）‎ ‎11．如图，大楼高30m，远处有一塔BC，某人爬到楼顶D测得塔顶的仰角为30°，且测得D、B相距30m，则塔高BC为（　　）m．‎ A．40 B．45 C．30+ D．30‎ ‎12．如图是二次函数y＝ax2+bx+c（a≠0）的图象，小明结合图象得到如下结论：①对称轴为直线x＝﹣1；②b2﹣4ac＞0；③方程ax2+bx+c＝0的解是x1＝﹣3，x2＝1；④不等式ax2+bx+c＞3的解为﹣2＜x＜0．其中正确结论的个数是（　　）‎ A．4个 B．3个 C．2个 D．1个 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎13．分解因式：a2﹣9＝　 　．‎ ‎14．已知方程5x2+kx﹣6＝0的一个根是2，则k的值为　 　．‎ ‎15．如图，以正五边形ABCDE的边CD为边作等边△CDF，使点F在其内部，连结FE，则∠DFE＝　 　°．‎ ‎16．若分式的值是2，则x＝　 　．‎ ‎17．甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系式；折线B﹣C﹣D﹣表示轿车离甲地距离y（千米）与x（小时）之间的函数关系，则货车出发　 　小时与轿车相遇．‎ ‎18．如图，矩形纸片ABCD，点O是BD的中点，点E是BC上的点，沿DE折叠后，点C恰好与点O重合，若CD＝3，则折痕DE的长为　 　．‎ 三、解答题（本大题共9个小题，共78分．请写出文字说明、证明过程或演算步骤）‎ ‎19．计算：32+（2﹣π）0﹣2cos45°．‎ ‎20．解不等式组：，并写出它的最小整数解．‎ ‎21．已知：▱ABCD的对角线AC与BD相交于点O，过点O的直线与AD，BC分别相交于点E，F，求证：OE＝OF．‎ ‎22．历下区某中学积极响应国家号召，落实垃圾“分类回收，科学处理“的政策，准备购买A、B两种型号的垃圾分类回收箱共20只，放在校园各个合适位置，以方便师生进行垃圾分类投放．学校共支付费用4240元，A、B型号价格信息如表：‎ 型号 价格 A型 ‎200元/只 B型 ‎240元/只 ‎（1）请问学校购买A型和B型垃圾回收箱各是多少只？‎ ‎（2）若学校都购买A型垃圾回收箱，能节省费用多少元？‎ ‎23．如图，在△ABC中，∠ABC＝60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点E，CE交⊙O于点D．‎ ‎（1）求∠ACD的度数；‎ ‎（2）若AC＝2，求DE的长；‎ ‎（3）在（2）的条件下，求图中阴影部分面积．‎ ‎24．为了遏制新型冠状病毒疫情的蔓延势头，各地教有部门在推迟各级学校开学时间的同时提出“停课不停学”的要求，各地学校也都开展了远程网络教学，历下区某校为学生提供四类在线学习方式：在线阅读、在线听课、在线答疑、在线讨论．为了了解学生的需求，该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如图两幅不完整的统计图．‎ 根据上面提供的信息，回答下列问题：‎ ‎（1）本次接受问卷调查的学生共有　 　人，在扇形统计图中“在线听课“所占的百分比为　 　，在扇形统计图中“在线讨论”所对应扇形圆心角为　 　度．‎ ‎（2）请补全条形统计图；‎ ‎（3）若该校共有800名学生，请你估计该校学生对“在线听课“和“在线答疑“感兴趣的共有多少人？‎ ‎（4）若九年级（1）班对“在线讨论“感兴趣的同学有3名男生和2名女生，班主任想从中随机挑选2名同学参加学校组织的疫情话题讨论活动，请用树状图法或列表法求出“至少1名女生”被选中参加话题讨论的概率．‎ ‎25．如图，正比例函数y＝kx与反比例函数y＝（m≠0）的图象交于A、B两点，点A的坐标为（1，2），点C为反比例函数图象第一象限上的一动点，连接OC、AC、BC．‎ ‎（1）求正比例函数与反比例函数的表达式；‎ ‎（2）作AD⊥y轴于点D，CE⊥x轴于点E，且OA＝OC时，求直线BC的函数表达式；‎ ‎（3）当△AOC是以OA为直角边的直角三角形时，求点C的坐标．‎ ‎26．直线m∥n，点A、B分别在直线m，n上（点A在点B的右侧），点P在直线m上，AP＝AB，连接BP，将线段BP绕点B顺时针旋转60°得到BC，连接AC交直线n于点E，连接PC，且△ABE为等边三角形．‎ ‎（1）如图①，当点P在A的右侧时，请直接写出∠ABP与∠EBC的数量关系是　 　，AP与EC的数量关系是　 　．‎ ‎（2）如图②，当点P在A的左侧时，（1）中的结论是否成立？若成立，请给予证明；若不成立，请说明理由．‎ ‎（3）如图②，当点P在A的左侧时，若△PBC的面积为，求线段AC的长．‎ ‎27．如图，抛物线y＝ax2+bx+3过A（﹣2，0）、B （6，0）两点，交y轴于点C，对称轴交x轴于点E，点D是其顶点，点H为x轴上一动点，连接CD、CH、DH．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）当点H与点B重合时，求△CDH的面积；‎ ‎（3）当DH⊥CD时，求点H的坐标．‎ 参考答案 一、选择题（本大题共12个小题，每小题4分，共48分。在每小题给出的四个选项中，只有一项是符合题目要求的。）‎ ‎1．64的平方根是（　　）‎ A．±8 B．±4 C．8 D．32‎ ‎【分析】直接根据平方根的定义即可求解．‎ 解：∵（±8）2＝64，‎ ‎∴64的平方根是±8，‎ 故选：A．‎ ‎2．如图，一个几何体由5个大小相同的正方体搭成，则这个立体图形的俯视图是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据从上边看得到的图形是俯视图，‎ 解：从上边看第一列是两个小正方形，第二列上层是一个小正方形，第三列上层是一个小正方形，‎ 故选：D．‎ ‎3．中国人民解放军海军山东舰是中国首艘自主建造的国产航母，该舰的满载排水量为67500吨，数字67500用科学记数法表示为（　　）‎ A．67.5×104 B．6.75×104 C．0.675×105 D．6.75×105‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．‎ 解：67500＝6.75×104．‎ 故选：B．‎ ‎4．如图，DE∥CF，∠1＝45°，∠2＝30°，则∠BDF等于（　　）‎ A．15° B．25° C．30° D．35°‎ ‎【分析】先根据平行线的性质求出∠CFD的度数，再由三角形外角的性质可得出结论．‎ 解：∵DE∥CF，∠2＝30°，‎ ‎∴∠CFD＝∠2＝30°．‎ ‎∵∠1＝45°，‎ ‎∴∠BDF＝∠1﹣∠CFD＝45°﹣30°＝15°．‎ 故选：A．‎ ‎5．若m＞n，则下列不等式正确的是（　　）‎ A．m+2＜n+2 B．m﹣2＜n﹣2 C．﹣2m＜﹣2n D．m2＞n2‎ ‎【分析】根据不等式的性质判断即可．‎ 解：∵m＞n，‎ ‎∴m+2＞n+2，m﹣2＞n﹣2，﹣2m＜﹣2n，‎ 故选：C．‎ ‎6．窗棂即窗格（窗里面的横的或竖的格）是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种花纹，构成种类繁多的优美图案，下列表示我国古代窗棂样式结构图案中既是轴对称图形又是中心对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据轴对称图形与中心对称图形的概念求解．‎ 解：A、不是轴对称图形，也是中心对称图形，故此选项不符合题意；‎ B、是轴对称图形，不是中心对称图形，故此选项不符合题意；‎ C、是轴对称图形，不是中心对称图形，故此选项不符合题意；‎ D、是轴对称图形，也是中心对称图形，故此选项符合题意．‎ 故选：D．‎ ‎7．若点A（x1，1）、B（x2，﹣2）、C（x3，﹣3）在反比例函数y＝﹣的图象上，则x1、x2、x3的大小关系是（　　）‎ A．x1＜x2＜x3 B．x1＜x3＜x2 C．x3＜x1＜x2 D．x2＜x1＜x3‎ ‎【分析】把三个点的坐标分别代入y＝﹣中，这样可计算出x1、x2、x3的值，从而可判断它们的大小．‎ 解：把A（x1，1）、B（x2，﹣2）、C（x3，﹣3）分别代入y＝﹣得1＝﹣，﹣2＝﹣‎ ‎，﹣3＝﹣，‎ 所以x1＝﹣1，x2＝，x3＝，‎ 所以x1＜x3＜x2．‎ 故选：B．‎ ‎8．如图，在平面直角坐标系xOy中，△ABC与△A1B1C1是中心对称图形．则对称中心的坐标是（　　）‎ A．（1，1） B．（1，0） C．（1，﹣1） D．（1，﹣2）‎ ‎【分析】连结AA1，CC1，两线交点即为对称中心．‎ 解：对称中心的坐标是（1，﹣1），‎ 故选：C．‎ ‎9．如图，统计图反映了我国2020年4月14日至20日新型冠状病毒肺炎全国国内新增确诊和新增境外输入确诊人数趋势，根据统计图提供的信息，下列推断合理的是（　　）‎ A．统计图中，新增境外输入确诊人数大于国内新增确诊人数的天数有3天 ‎ B．4月15日，我国新增境外输入确诊人数比国内新增确诊人数的1.9倍还多 ‎ C．4月14日至20日，我国新增境外输入确诊人数的中位数是17例 ‎ D．4月14日至20日，我国国内新增确诊人数的平均数是15例 ‎【分析】根据折线统计图所反映的数据，逐个选项进行判断即可．‎ 解：从统计图中科员看出，新增境外输入确诊人数大于国内新增确诊人数的天数为4天，不是3天，因此选项A不正确；‎ ‎4月15日，新增境外输入病例为34例，而国内新增确诊为18例，34÷18≈1.88（倍），因此选项B不正确；‎ 将14日﹣20日，新增境外输入确诊病例从小到大排列后，处在第4位是17例，中位数是17，因此选项C正确；‎ ‎（13+18+12+14+12+28+9）÷7≈15.2，因此选项D不正确；‎ 故选：C．‎ ‎10．在平面直角坐标系中，对于点P（x，y），我们把点P'（1﹣y，x﹣1）叫做点P的友好点，已知点A1的友好点为A2，点A2的友好点为A3，点A3的友好点为A4……，这样依次得到点A1，A2，A3，A4……，若点A1的坐标为（2，1），则点A2020的坐标为（　　）‎ A．（2，1） B．（0，1） C．（0，﹣1） D．（2，﹣1）‎ ‎【分析】根据友好点的定义及点A1的坐标为（2，1），顺次写出几个友好点的坐标，可发现循环规律，据此可解．‎ 解：∵点A1的坐标为（2，1），‎ ‎∴根据友好点的定义可得：A1（2，1），A2（0，1），A3（0，﹣1），A4（2，﹣1），A5（2，1），A6（0，1），‎ ‎∴以此类推，每4个点为一个循环，‎ ‎∵2020÷4＝505，‎ ‎∴点A2020的坐标与A4的坐标相同，为（2，﹣1）．‎ 故选：D．‎ ‎11．如图，大楼高30m，远处有一塔BC，某人爬到楼顶D测得塔顶的仰角为30°，且测得D、B相距30m，则塔高BC为（　　）m．‎ A．40 B．45 C．30+ D．30‎ ‎【分析】过点D作DE⊥BC于点E，由直角三角形的性质求出BE＝15m，则可得出答案．‎ 解：过点D作DE⊥BC于点E，‎ ‎∵∠BDE＝30°，BD＝30m，‎ ‎∴BE＝BD＝15m，‎ ‎∵AD＝30m，‎ ‎∴CE＝30m，‎ ‎∴BC＝CE+BE＝30+15＝45m．‎ 故选：B．‎ ‎12．如图是二次函数y＝ax2+bx+c（a≠0）的图象，小明结合图象得到如下结论：①对称轴为直线x＝﹣1；②b2﹣4ac＞0；③方程ax2+bx+c＝0的解是x1＝﹣3，x2＝1；④不等式ax2+bx+c＞3的解为﹣2＜x＜0．其中正确结论的个数是（　　）‎ A．4个 B．3个 C．2个 D．1个 ‎【分析】利用抛物线与x轴的交点为对称点可对①进行判断；利用抛物线与x轴有2个交点可对②进行判断；根据x＝﹣3时，y＝0；x＝1时，y＝0可对③进行判断；抛物线的对称性得到点（0，3）关于直线x＝﹣1的对称点为（﹣2，0），然后利用函数图象可对④进行判断．‎ 解：∵抛物线经过点（﹣3，0），（1，0），‎ ‎∴抛物线的对称轴为直线x＝＝﹣1，所以①正确；‎ ‎∵抛物线与x轴有2个交点，‎ ‎∴△＝b2﹣4ac＞0，所以②正确；‎ ‎∵x＝﹣3时，y＝0；x＝1时，y＝0，‎ ‎∴方程ax2+bx+c＝0的解是x1＝﹣3，x2＝1，所以③正确；‎ ‎∵点（0，3）关于直线x＝﹣1的对称点为（﹣2，0），‎ ‎∴当﹣2＜x＜0时，y＞3，‎ 即不等式ax2+bx+c＞3的解为﹣2＜x＜0，所以④正确．‎ 故选：A．‎ 二、填空题（本大题共6小题，每小题4分，共24分）‎ ‎13．分解因式：a2﹣9＝　（a+3）（a﹣3）　．‎ ‎【分析】直接利用平方差公式分解因式进而得出答案．‎ 解：a2﹣9＝（a+3）（a﹣3）．‎ 故答案为：（a+3）（a﹣3）．‎ ‎14．已知方程5x2+kx﹣6＝0的一个根是2，则k的值为　﹣7　．‎ ‎【分析】把方程的根代入方程可以求出字母系数的值．‎ 解：把2代入方程有：5×4+2k﹣6＝0‎ 解得：k＝﹣7．‎ 故答案为：﹣7．‎ ‎15．如图，以正五边形ABCDE的边CD为边作等边△CDF，使点F在其内部，连结FE，则∠DFE＝　66　°．‎ ‎【分析】根据等边三角形的性质和多边形的内角和解答即可．‎ 解：因为△CDF是等边三角形，‎ 所以∠CDF＝60°，‎ 因为∠CDE＝（5﹣2）×180°÷5＝108°，‎ 所以∠EDF＝108°﹣60°＝48°，‎ 因为DE＝DF，‎ 所以∠DFE＝（180°﹣48°）÷2＝66°．‎ 故答案为：66．‎ ‎16．若分式的值是2，则x＝　4　．‎ ‎【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．‎ 解：根据题意得：＝2，‎ 去分母得：x﹣6＝2x﹣10，‎ 解得：x＝4，‎ 经检验x＝4是分式方程的解．‎ 故答案为：4．‎ ‎17．甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系式；折线B﹣C﹣D﹣表示轿车离甲地距离y（千米）与x（小时）之间的函数关系，则货车出发　3.9　小时与轿车相遇．‎ ‎【分析】根据函数图象中的数据，可以分别求得OA段和CD 对应的函数解析式，然后令它们相等，求得x的值，即可得到货车出发几小时与轿车相遇．‎ 解：设OA段对应的函数解析式为y＝kx，‎ 将（5，300）代入，得：5k＝300，‎ 解得k＝60，‎ 即OA段对应的函数解析式为y＝60x，‎ 设CD段对应的函数解析式为y＝ax+b，‎ ‎，‎ 解得，‎ 即CD段对应的函数解析式为y＝110x﹣195，‎ 令110x﹣195＝60x，得x＝3.9，‎ 即货车出发3.9小时与轿车相遇，‎ 故答案为：3.9．‎ ‎18．如图，矩形纸片ABCD，点O是BD的中点，点E是BC上的点，沿DE折叠后，点C恰好与点O重合，若CD＝3，则折痕DE的长为　2　．‎ ‎【分析】根据图形翻折变换的性质求出OD，那么BD＝2OD，在Rt△DBC中由勾股定理求出BC，在Rt△BOE中，设OE＝x，利用勾股定理求出x，然后根据DE＝BE＝BC﹣CE即可得出结论．‎ 解：∵△OED是△CED翻折而成，‎ ‎∴OD＝CD＝3，OE＝CE，∠DOE＝∠C＝90°，‎ ‎∴EO⊥BD，‎ 又∵点O是BD的中点，‎ ‎∴BD＝2OD＝2×3＝6，BE＝DE，‎ 在Rt△DBC中，BD2＝CD2+BC2，‎ 即62＝32+BC2，解得BC＝3，‎ 在Rt△BOE中，设OE＝x，则BE＝3﹣x，‎ BE2＝BO2+OE2，即（3﹣x）2＝32+x2，解得x＝，‎ ‎∴DE＝BE＝BC﹣CE＝3﹣＝2，‎ 故答案为：2．‎ 三、解答题（本大题共9个小题，共78分．请写出文字说明、证明过程或演算步骤）‎ ‎19．计算：32+（2﹣π）0﹣2cos45°．‎ ‎【分析】原式利用乘方的意义，零指数幂法则，绝对值的代数意义，以及特殊角的三角函数值计算即可求出值．‎ 解：原式＝9+﹣1﹣1﹣2×‎ ‎＝9+﹣1﹣1﹣‎ ‎＝7．‎ ‎20．解不等式组：，并写出它的最小整数解．‎ ‎【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．‎ 解：‎ 解不等式①得：x＞﹣4，‎ 解不等式②得：x≥﹣1，‎ 则不等式组的解集为x≥﹣1，‎ 所以不等式组的最小整数解为﹣1．‎ ‎21．已知：▱ABCD的对角线AC与BD相交于点O，过点O的直线与AD，BC分别相交于点E，F，求证：OE＝OF．‎ ‎【分析】由四边形ABCD是平行四边形，根据平行四边形对角线互相平分，即可得OA＝OC，又由OE⊥AD，OF⊥BC，易证得△AEO≌△CFO，由全等三角形的对应边相等，可得OE＝OF．‎ ‎【解答】证明：∵四边形ABCD是平行四边形，‎ ‎∴OA＝OC，AD∥BC，‎ ‎∴∠EAO＝∠FCO，‎ ‎∵OE⊥AD，OF⊥BC，‎ ‎∴∠AEO＝∠CFO＝90°，‎ 在△AEO和△CFO中，，‎ ‎∵∴△AEO≌△CFO（AAS），‎ ‎∴OE＝OF．‎ ‎22．历下区某中学积极响应国家号召，落实垃圾“分类回收，科学处理“的政策，准备购买A、B两种型号的垃圾分类回收箱共20只，放在校园各个合适位置，以方便师生进行垃圾分类投放．学校共支付费用4240元，A、B型号价格信息如表：‎ 型号 价格 A型 ‎200元/只 B型 ‎240元/只 ‎（1）请问学校购买A型和B型垃圾回收箱各是多少只？‎ ‎（2）若学校都购买A型垃圾回收箱，能节省费用多少元？‎ ‎【分析】（1）设学校购买A型垃圾回收箱x只，购买B型垃圾回收箱y只，根据学校购买两种型号的垃圾回收箱共20只且共花费4240元，即可得出关于x，y的二元一次方程组，解之即可得出结论；‎ ‎（2）根据节省的总费用＝每只节省的费用×购买B型垃圾回收箱的数量，即可求出结论．‎ 解：（1）设学校购买A型垃圾回收箱x只，购买B型垃圾回收箱y只，‎ 依题意，得：，‎ 解得：．‎ 答：学校购买A型垃圾回收箱14只，购买B型垃圾回收箱6只．‎ ‎（2）（240﹣200）×6＝240（元）．‎ 答：能节省费用240元．‎ ‎23．如图，在△ABC中，∠ABC＝60°，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点E，CE交⊙O于点D．‎ ‎（1）求∠ACD的度数；‎ ‎（2）若AC＝2，求DE的长；‎ ‎（3）在（2）的条件下，求图中阴影部分面积．‎ ‎【分析】（1）连接AD，根据圆周角定理得到∠CAD＝90°，∠ADC＝∠ABC＝60°，根据直角三角形的性质计算，得到答案；‎ ‎（2）连接OA，根据余弦的定义求出CD，根据切线的性质得到∠OAE＝90°，根据直角三角形的性质计算即可；‎ ‎（3）根据三角形的面积公式、扇形面积公式计算，得到答案．‎ 解：（1）连接AD，‎ ‎∵CD是⊙O的直径，‎ ‎∴∠CAD＝90°，‎ 由圆周角定理得，∠ADC＝∠ABC＝60°，‎ ‎∴∠ACD＝90°﹣60°＝30°；‎ ‎（2）连接OA，‎ 在Rt△ACD中，CD＝＝4，‎ ‎∵AE是⊙O的切线，‎ ‎∴∠OAE＝90°，‎ 由圆周角定理得，∠AOD＝2∠ACD＝60°，‎ ‎∴∠E＝30°，‎ ‎∴OE＝2OA＝4，‎ ‎∴DE＝OE﹣OD＝2；‎ ‎（3）在Rt△OAE中，AE＝OE•cosE＝2，‎ ‎∴阴影部分的面积＝×2×2﹣＝2﹣π．‎ ‎24．为了遏制新型冠状病毒疫情的蔓延势头，各地教有部门在推迟各级学校开学时间的同时提出“停课不停学”的要求，各地学校也都开展了远程网络教学，历下区某校为学生提供四类在线学习方式：在线阅读、在线听课、在线答疑、在线讨论．为了了解学生的需求，该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如图两幅不完整的统计图．‎ 根据上面提供的信息，回答下列问题：‎ ‎（1）本次接受问卷调查的学生共有　100　人，在扇形统计图中“在线听课“所占的百分比为　40%　，在扇形统计图中“在线讨论”所对应扇形圆心角为　54　度．‎ ‎（2）请补全条形统计图；‎ ‎（3）若该校共有800名学生，请你估计该校学生对“在线听课“和“在线答疑“感兴趣的共有多少人？‎ ‎（4）若九年级（1）班对“在线讨论“感兴趣的同学有3名男生和2名女生，班主任想从中随机挑选2名同学参加学校组织的疫情话题讨论活动，请用树状图法或列表法求出“至少1名女生”被选中参加话题讨论的概率．‎ ‎【分析】（1）由在线阅读人数及其所占百分比求出总人数，用在线听课人数除以总人数可得其对应百分比，用360°乘以在线讨论人数所占比例可得其对应圆心角度数；‎ ‎（2）根据四种方式的人数之和等于总人数求出在线答疑人数，从而补全图形；‎ ‎（3）用总人数乘以样本中在线听课和在线答疑人数所占比例可得答案；‎ ‎（4）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与选出的至少有1名女生的情况数，再利用概率公式即可求得答案．‎ 解：（1）本次接受问卷调查的学生共有25÷25%＝100（人），‎ 在扇形统计图中“在线听课“所占的百分比为×100%＝40%，‎ 在扇形统计图中“在线讨论“所对应扇形圆心角为360°×＝54°，‎ 故答案为：100、40%、54；‎ ‎（2）在线答疑对应的人数为100﹣（25+40+15）＝20（人），‎ 补全条形图如下：‎ ‎（3）估计该校学生对“在线听课“和“在线答疑“感兴趣的共有800×＝480（人）；‎ ‎（4）画树状图为：‎ 共有20种等可能的结果数，其中“至少1名女生”被选中参加话题讨论的有14种结果，‎ 所以“至少1名女生”被选中参加话题讨论的概率为＝．‎ ‎25．如图，正比例函数y＝kx与反比例函数y＝（m≠0）的图象交于A、B两点，点A的坐标为（1，2），点C为反比例函数图象第一象限上的一动点，连接OC、AC、BC．‎ ‎（1）求正比例函数与反比例函数的表达式；‎ ‎（2）作AD⊥y轴于点D，CE⊥x轴于点E，且OA＝OC时，求直线BC的函数表达式；‎ ‎（3）当△AOC是以OA为直角边的直角三角形时，求点C的坐标．‎ ‎【分析】（1）将点A的坐标分别代入y＝kx和y＝，即可求解；‎ ‎（2）点B（﹣1，﹣2），反比例函数的图象关于直线y＝x对称且OA＝OC，则点A、C关于直线y＝x对称，过点C（2，1），即可求解；‎ ‎（3）直线AB的表达式为：y＝2x，则tan∠AOC＝2，则tan∠ANO＝，求出直线AC 的表达式为：y＝﹣x+，即可求解．‎ 解：（1）将点A的坐标分别代入y＝kx和y＝并解得：k＝2，m＝2，‎ 故正比例函数与反比例函数的表达式分别为：y＝2x，y＝①；‎ ‎（2）∵反比例函数的图象关于原点成中心对称，故点B（﹣1，﹣2），‎ ‎∵反比例函数的图象关于直线y＝x对称且OA＝OC，‎ ‎∴点A、C关于直线y＝x对称，过点C（2，1），‎ 设直线BC的表达式为：y＝tx+s，则，解得，‎ 故直线BC的表达式为：y＝x﹣1；‎ ‎（3）如下图，延长AC交x、y轴于点M、N，‎ 直线AB的表达式为：y＝2x，则tan∠AOC＝2，‎ 当△AOC是以OA为直角边的直角三角形时，即∠OAC＝90°，‎ 则tan∠ANO＝，‎ 故设直线AC的表达式为：y＝﹣x+r，‎ 将点A的坐标代入上式并解得：r＝，‎ 故直线AC的表达式为：y＝﹣x+②，‎ 联立①②并解得：x＝1（舍去）或4，‎ 故点C（4，）．‎ ‎26．直线m∥n，点A、B分别在直线m，n上（点A在点B的右侧），点P在直线m上，AP＝AB，连接BP，将线段BP绕点B顺时针旋转60°得到BC，连接AC交直线n于点E，连接PC，且△ABE为等边三角形．‎ ‎（1）如图①，当点P在A的右侧时，请直接写出∠ABP与∠EBC的数量关系是　∠ABP＝∠EBC　，AP与EC的数量关系是　AP＝EC　．‎ ‎（2）如图②，当点P在A的左侧时，（1）中的结论是否成立？若成立，请给予证明；若不成立，请说明理由．‎ ‎（3）如图②，当点P在A的左侧时，若△PBC的面积为，求线段AC的长．‎ ‎【分析】（1）根据等边三角形的性质得到∠ABE＝60°，AB＝BE，根据旋转的性质得到∠CBP＝60°，BC＝BP，根据全等三角形的性质得到结论；‎ ‎（2）根据等边三角形的性质得到∠ABE＝60°，AB＝BE，根据旋转的性质得到∠CBP＝60°，BC＝BP，根据全等三角形的性质得到结论；‎ ‎（3）过点C作CD⊥m于D，根据旋转的性质得到△PBC是等边三角形，求得PC＝3，设AP＝CE＝t，则AB＝AE＝3t，得到AC＝2t，根据平行线的性质得到∠CAD＝∠AEB＝60°，解直角三角形即可得到结论．‎ 解：（1）∵△ABE是等边三角形，‎ ‎∴∠ABE＝60°，AB＝BE，‎ ‎∵将线段BP绕点B顺时针旋转60°得到BC，‎ ‎∴∠CBP＝60°，BC＝BP，‎ ‎∴∠ABP＝60°﹣∠PBE，∠CBE＝60°﹣∠PBE，‎ 即∠ABP＝∠EBC，‎ ‎∴△ABP≌△EBC（SAS），‎ ‎∴AP＝EC；‎ 故答案为：∠ABP＝∠EBC，AP＝EC；‎ ‎（2）存在，∵△ABE是等边三角形，‎ ‎∴∠ABE＝60°，AB＝BE，‎ ‎∵将线段BP绕点B顺时针旋转60°得到BC，‎ ‎∴∠CBP＝60°，BC＝BP，‎ ‎∴∠ABP＝60°﹣∠PBE，∠CBE＝60°﹣∠PBE，‎ 即∠ABP＝∠EBC，‎ ‎∴△ABP≌△EBC（SAS），‎ ‎∴AP＝EC；‎ ‎（3）过点C作CD⊥m于D，‎ ‎∵将线段BP绕点B顺时针旋转60°得到BC，‎ ‎∴△PBC是等边三角形，‎ ‎∴PC2＝，‎ ‎∴PC＝3，‎ 设AP＝CE＝t，则AB＝AE＝3t，‎ ‎∴AC＝2t，‎ ‎∵m∥n，‎ ‎∴∠CAD＝∠AEB＝60°，‎ ‎∴AD＝AC＝t，CD＝AD＝t，‎ ‎∵PD2+CD2＝PC2，‎ ‎∴（2t）2+3t2＝9，‎ ‎∴t＝（负值舍去），‎ ‎∴AC＝2t＝．‎ ‎27．如图，抛物线y＝ax2+bx+3过A（﹣2，0）、B （6，0）两点，交y轴于点C，对称轴交x轴于点E，点D是其顶点，点H为x轴上一动点，连接CD、CH、DH．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）当点H与点B重合时，求△CDH的面积；‎ ‎（3）当DH⊥CD时，求点H的坐标．‎ ‎【分析】（1）根据待定系数法求得即可；‎ ‎（2）先求得直线BC的解析式，即可求得直线BC与对称轴的交点坐标，然后根据S△CDH＝S△CDF+S△BDF求得即可；‎ ‎（3）过D作DM⊥y轴于M，过H点作HN⊥DM于N，易证得△DCM∽△HDN，根据相似三角形的性质得出，解得DN＝2，即可求得OH＝MN＝4．‎ 解：（1）抛物线y＝ax2+bx+3过A（﹣2，0）、B （6，0）两点，‎ ‎∴，‎ 解得，‎ ‎∴抛物线为y＝﹣x2+x+3；‎ ‎（2）当x＝0时，y＝3，‎ 解C（0，3），‎ 设直线BC的解析式为y＝kx+c，‎ 把B（6，0）、C（0，3）代入得，解得，‎ ‎∴直线BC的解析式为y＝﹣+3，‎ 设对称轴DE交BC于点F，则F（2，2），‎ ‎∵D（2，4），‎ ‎∴DF＝2，‎ ‎∴S△CDH＝＝6；‎ ‎（3）如图，过D作DM⊥y轴于M，过H点作HN⊥DM于N，则∠CMD＝∠DNH＝90°，‎ ‎∵DH⊥CD，‎ ‎∴∠MCD+∠MDC＝∠MDC+∠NDH＝90°，‎ ‎∴∠MCD＝∠NDH，‎ ‎∴△DCM∽△HDN，‎ ‎∴，‎ ‎∵D（2，4），C（0，3），‎ ‎∴DM＝2，MC＝1，HN＝4，‎ ‎∴，解得DN＝2，‎ ‎∴OH＝MN＝4，‎ ‎∴H（4，0）．‎