2012年福建省三明市初中毕业暨高级中等学校招生统一考试（含答案）

2012年福建省三明市初中毕业暨高级中等学校招生统一考试（含答案）

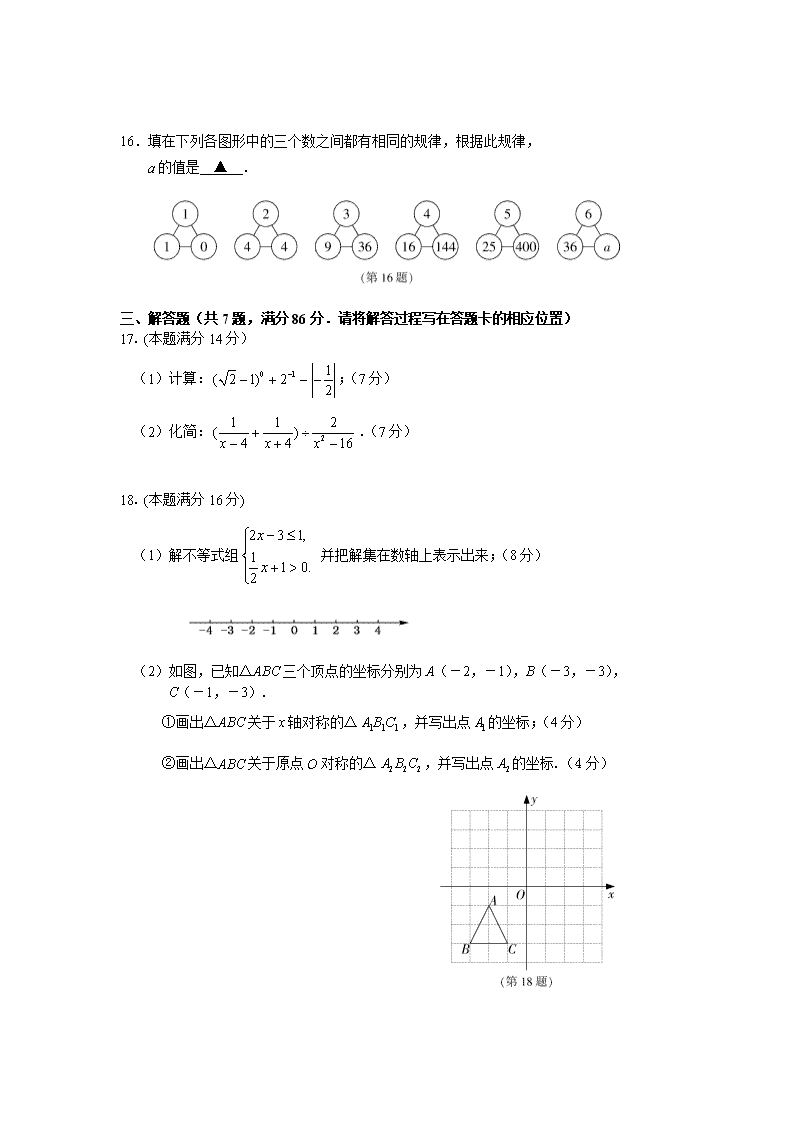
‎2012年三明市初中毕业暨高级中等学校招生统一考试 数 学 试 题 ‎（满分：150分 考试时间：120分钟）‎ 友情提示：‎ ‎1.作图或画辅助线等需用签字笔描黑.‎ ‎2.未注明精确度的计算问题，结果应为准确数.‎ ‎3.抛物线()的顶点坐标为，对称轴.‎ 一、选择题（共10小题，每小题4分，满分40分.每小题只有一个正确选项，请在答题卡 的相应位置填涂）‎ ‎1. 在－2，－，0，2四个数中，最大的数是( ▲ )‎ A. －2 B. － C. 0 D. 2‎ ‎2．据《2011年三明市国民经济和社会发展统计公报》数据显示，截止2011年末三明市 常住人口约为2 510 000人，2 510 000用科学记数法表示为（▲）‎ A． B． ‎ C． Ｄ． ‎ ‎3．如图，AB//CD，∠CDE=，则∠A的度数为（▲）‎ A． B． 　　 C．　 　D．‎ ‎4．分式方程的解是(▲) ‎ A． B． C． D．‎ ‎5．右图是一个由相同小正方体搭成的几何体的俯视图，小正方形中的数字表示在该位置上的小正方体的个数，则这个几何体的左视图是（▲）‎ ‎ ‎ ‎6．一个多边形的内角和是，则这个多边形的边数为（▲）‎ ‎ A．4 B．5 C．6 D．7‎ ‎7．下列计算错误的是(▲)‎ A． B． C． D．‎ ‎8．如图，AB是⊙O的切线，切点为A，OA=1，∠AOB=，则图 中阴影部分的面积是（▲）‎ A． B．‎ C． D．‎ ‎9．在一个不透明的盒子里有3个分别标有数字5，6，7的小球，它们 除数字外其他均相同．充分摇匀后，先摸出1个球不放回，再摸出 ‎1个球，那么这两个球上的数字之和为奇数的概率为（▲） ‎ ‎ A． B． C． D．‎ ‎10．如图，在平面直角坐标系中，点A在第一象限，点P在轴上，‎ 若以P，O，A为顶点的三角形是等腰三角形，则满足条件的 点P共有（▲）‎ A． 2个 B． 3个 C．4个 D．5个 二、填空题（共6小题，每小题4分，满分24分．请将答案填在答题卡的相应位置）‎ ‎11．分解因式：= ▲ ．‎ ‎12．如图，在△ABC中，D，E分别是边AB，AC的中点，‎ 若BC=6，则DE= ▲ ．‎ ‎13．某校九（1）班6位同学参加跳绳测试，他们的成绩 ‎（单位：次/分钟）分别为：173，160，168，166，175，‎ ‎168．这组数据的众数是 ▲ ．‎ ‎14．如图，在△ABC中，D是BC边上的中点，∠BDE=∠CDF，‎ 请你添加一个条件，使DE=DF成立．你添加的条件是 ▲ ．‎ ‎(不再添加辅助线和字母)‎ ‎15．如图，点A在双曲线上，点B在双曲线 上，且AB//轴，点P是轴上的任意一点，‎ 则△PAB的面积为 ▲ ． ‎ ‎16．填在下列各图形中的三个数之间都有相同的规律，根据此规律，‎ a的值是 ▲ ．‎ 三、解答题（共7题，满分86分．请将解答过程写在答题卡的相应位置）‎ ‎17. (本题满分14分）‎ ‎（1）计算：；（7分）‎ ‎（2）化简：．（7分）‎ ‎18. (本题满分16分)‎ ‎（1）解不等式组 并把解集在数轴上表示出来；（8分）　‎ ‎（2）如图，已知△ABC三个顶点的坐标分别为A（－2，－1），B（－3，－3），‎ C（－1，－3）.‎ ‎①画出△ABC关于轴对称的△，并写出点的坐标；（4分）‎ ‎②画出△ABC关于原点O对称的△，并写出点的坐标.（4分）‎ ‎19. (本题满分10分)‎ 为了解某县2012年初中毕业生数学质量检测成绩等级的分布情况，随机抽取了该县若干名初中毕业生的数学质量检测成绩，按A，B，C，D四个等级进行统计分析，并绘制了如下尚不完整的统计图：‎ 请根据以上统计图提供的信息，解答下列问题：‎ ‎（1）本次抽取的学生有___▲ 名；（2分）‎ ‎（2）补全条形统计图；（2分）‎ ‎（3）在抽取的学生中C级人数所占的百分比是__▲ ；（2分）‎ ‎（4）根据抽样调查结果，请你估计2012年该县1430名初中毕业生数学质量检测成绩为A级的人数．（4分）‎ ‎20．(本题满分10分)‎ ‎ 某商店销售A，B两种商品，已知销售一件A种商品可获利润10元，销售一件B种商品可获利润15元．‎ ‎（1）该商店销售A，B两种商品共100件，获利润1350元，则A，B两种商品各销售多少件？（5分）‎ ‎（2）根据市场需求，该商店准备购进A，B两种商品共200件，其中B种商品的件数 不多于A种商品件数的3倍．为了获得最大利润，应购进A，B两种商品各多少件？可获得最大利润为多少元？（5分）‎ ‎21. (本题满分10分)‎ 如图，在△ABC中，点O在AB上，以O为圆心的圆 经过A，C两点，交AB于点D，已知∠A=，∠B=，‎ 且2+=．‎ ‎ （1）求证：BC是⊙O的切线；（5分）‎ ‎（2）若OA=6，，求BC的长．（5分）‎ ‎22．（本题满分12分）‎ 已知直线与轴和轴分别交于点A和点B，抛物线的顶点M在直线AB上，且抛物线与直线AB的另一个交点为N．‎ ‎（1）如图①，当点M与点A重合时，求：‎ ‎①抛物线的解析式；（4分）‎ ‎②点N的坐标和线段MN的长；（4分）‎ ‎（2）抛物线在直线AB上平移，是否存在点M，使得△OMN与△AOB相似？若存在，直接写出点M的坐标；若不存在，请说明理由．（4分）‎ ‎23．（本题满分14分）‎ 在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），‎ ‎∠BPE＝∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．‎ ‎（1） 当点P与点C重合时（如图①）．求证：△BOG≌△POE；（4分）‎ ‎（2）通过观察、测量、猜想：= ▲ ，并结合图②证明你的猜想；（5分）‎ ‎（3）把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=，‎ 求的值．（用含的式子表示）（5分） ‎ ‎2012年三明市初中毕业暨高级中等学校招生统一考试 数学试卷参考答案及评分标准 说明：以下各题除本参考答案提供的解法外，其他解法参照本评分标准，按相应给分点评分.‎ 一、选择题(每小题4分，共40分)‎ ‎1. D 2. C 3. D 4. A 5. B 6. C 7. B 8. C 9. A 10. C 二、填空题（每小题4分，共24分）‎ ‎11. 12. 3 13. 168 14. 答案不唯一；如：AB=AC；或∠B=∠C；‎ 或∠BED=∠CFD；或∠AED=∠AFD等；15. 1 16. 900‎ 三、解答题（共86分）‎ ‎17．（1）解：原式= ……………6分 ‎ =1. ……………7分 ‎（2）解法一：原式= ……………2分 ‎ = ……………6分 ‎ =. ……………7分 ‎ 解法二：原式= ……………4分 ‎ = ……………6分 ‎ =. ……………7分 ‎ ‎18．解：（1）解不等式①，得 ， ……………2分 解不等式②，得 -2. ……………4分 ‎ 不等式①，②的解集在数轴上表示如下：‎ ‎ ……………6分 ‎ ‎ 所以原不等式组的解集为． ……………8分 ‎（2）①如图所示，；‎ 画图正确3分，坐标写对1分；‎ ‎②如图所示，． ‎ 画图正确3分，坐标写对1分；‎ ‎19．解：（1）100； …………2分 ‎（2）如图所示； …………4分 ‎ （3）30%； …………6分 ‎ （4）1430×20%＝286（人） …………9分 ‎ 答：成绩为A级的学生人数约为286人．…10分 ‎20．解：（1）解法一：设A种商品销售x 件，‎ 则B种商品销售（100- x）件． ……………1分 ‎ 依题意，得 ……………3分 ‎ 解得x=30．∴ 100- x =70． ……………4分 ‎ 答：A种商品销售30件，B种商品销售70件. ……………5分 ‎ 解法二：设A种商品销售x 件， B种商品销售y件． ……1分 ‎ 依题意，得 ……………3分 ‎ 解得 ……………4分 ‎ 答：A种商品销售30件，B种商品销售70件. ……………5分 ‎（2）设A种商品购进x 件，则B种商品购进（200- x）件． ………6分 依题意，得0≤ 200- x ≤3x 解得 50≤x≤200 ……………7分 ‎ 设所获利润为w元，则有 w=10x+15（200- x）= - 5x +3000 ……………8分 ‎∵- 5＜0，∴w随x的增大而减小. ‎ ‎∴当x=50时，所获利润最大 ‎=2750元. ……………9分 ‎ 200- x=150.‎ ‎ 答：应购进A种商品50件，B种商品150件，‎ 可获得最大利润为2750元. ……………10分 ‎21.(1)证明:证法一：连接OC(如图①)，∴∠BOC =2∠A=2， ……2分 ‎∴∠BOC+∠B=2+=90．∴∠BCO=90．即OC⊥BC． ……4分 ‎∴BC是的⊙O切线． ……5分 证法二：连接OC(如图①)， ∵ OA=OC ， . ‎ ‎ ∴∠ACO =∠A =． ……1分 ‎ ∵ ∠BOC =∠A+∠ACO=2， ……2分 ‎ ∴∠BOC+∠B=2+=90． ……3分 ‎ ∴∠BCO=90．即OC⊥BC． ……4分 ‎ ‎∴BC是的⊙O切线． ……5分 证法三：连接OC(如图①)，‎ ‎∵OA=OC，∴∠OCA=∠A=. ……1分 在△ACB中，‎ ‎∠ACB=－（∠A+∠B）=－（+）‎ ‎∴∠BCO=∠ACB－∠ACO =－（+）－‎ ‎ =－（2+）. ……3分 ‎∵2+=90,∴∠BCO.即OC⊥BC． ……4分 ‎∴BC是⊙O的切线. ……5分 证法四：连接OC，延长BC(如图②)，‎ ‎∴∠ACE=∠A+∠B=+. …… 1分 又∵OA=OC，∴∠OCA=∠A=. …… 2分 ‎∴∠OCE=∠OCA+∠ACE=++=2+=. … 4分 即OC⊥BC.∴BC是⊙O的切线. … 5分 证法五：过点A作AE⊥BC，交BC的延长线于点E，连接OC(如图③)，‎ 在△AEB中，∠EAB+∠B=90. …… 1分 ‎∵∠CAB=，∠B=，且 2+=90，‎ ‎∴∠EAB=2.∴∠EAC=∠CAB=. …… 2分 ‎∵OC=OA,‎ ‎∴∠OAC=∠OCA=，∠EAC=∠OCA. …… 3分 ‎∴OC//AE. ∴OC⊥BC. …… 4分 ‎∴BC是⊙O的切线. …… 5分 ‎(2)∵OC=OA =6，由(1)知，OC⊥BC，在△BOC中，‎ ‎=，∵=，∴=． …… 8分 ‎∴OB=10． …… 9分 ‎∴BC===8． …… 10分 ‎22．（1）解：①∵直线与轴和 轴交于点A和点B，‎ ‎∴，． ……1分 解法一：当顶点M与点A重合时，∴. ……2分 ‎∴抛物线的解析式是：．即． ……4分 解法二：当顶点M与点A重合时，∴. ……2分 ‎∵ ， ∴. ‎ 又∵，∴. ……3分 ‎∴抛物线的解析式是：． ……4分 ‎②∵N在直线上，设，又N在抛物线上，‎ ‎∴． ……5分 解得 ， （舍去）‎ ‎∴． ……6分 过N作NC⊥轴，垂足为C(如图①)．‎ ‎∵，∴．‎ ‎∴． ． ……7分 ‎∴． ……8分 ‎（2）存在.‎ ‎ ………………10分 ‎ . ………………12分 ‎23.（1）证明：∵四边形ABCD是正方形，P与C重合,‎ ‎∴OB=OP ， ∠BOC=∠BOG=90°． ……2分 ‎∵PF⊥BG ，∠PFB=90°，‎ ‎∴∠GBO=90°—∠BGO，∠EPO=90°—∠BGO，‎ ‎∴∠GBO=∠EPO ． ……3分 ‎∴△BOG≌△POE． ……4分 ‎（2）． ……5分 证明：如图②，过P作PM//AC交BG于M，交BO于N，‎ ‎∴∠PNE=∠BOC=90°， ∠BPN=∠OCB．‎ ‎∵∠OBC=∠OCB =， ∴ ∠NBP=∠NPB．‎ ‎∴NB=NP．‎ ‎∵∠MBN=90°—∠BMN， ∠NPE=90°—∠BMN，‎ ‎∴∠MBN=∠NPE． ……6分 ‎∴△BMN≌△PEN． ……7分 ‎∴BM=PE．∵∠BPE=∠ACB， ∠BPN=∠ACB，‎ ‎∴∠BPF=∠MPF．‎ ‎∵PF⊥BM，∴∠BFP=∠MFP=. 又PF=PF， ‎ ‎∴△BPF≌△MPF． ……8分 ‎∴BF=MF ． 即BF=BM．∴BF=PE ． 即． ……9分 ‎（3）解法一：如图③，过P作PM//AC交BG于点M，交BO于点N，‎ ‎∴∠BPN=∠ACB=，∠PNE=∠BOC=90°. ……10分 由（2）同理可得BF=BM， ∠MBN=∠EPN． ……11分 ‎∵∠BNM=∠PNE=90°， ‎ ‎∴△BMN∽△PEN． ……12分 ‎∴． ……13分 在△BNP中，， ‎ ‎∴．即．‎ ‎∴． ……14分 解法二：如图③，过P作PM//AC交BG于点M，交BO于点N，‎ ‎∴BO⊥PM，∠BPN=∠ACB=. ……10分 ‎∵∠BPE=∠ACB=，PF⊥BM，‎ ‎∴∠EPN=. ∠MBN=∠EPN=∠BPE=. ‎ 设，‎ 在△PFB中， ， ……11分 ‎∵PF=PE+EF=，∴ ……12分 在△BFE中，， ∴.‎ ‎∴. .‎ ‎. ……13分 ‎∴ . 即. ……14分 解法三：如图③，过P作PM//AC交BG于点M，交BO于点N，‎ ‎∴ ∠BNP=∠BOC=90°.‎ ‎∴ ∠EPN+∠NEP=90°.‎ 又∵BF⊥PE，∴ ∠FBE+∠BEF=90°.‎ ‎∵∠BEF=∠NEP，∴ ∠FBE=∠EPN. …… 10分 ‎∵PN//AC，∴∠BPN=∠BCA=.‎ 又∵∠BPE=∠ACB=，∴∠NPE=∠BPE=.‎ ‎∴∠FBE=∠BPE=∠EPN=.‎ ‎∵ ，∴ . …… 11分 ‎∵ ，∴ . …… 12分 ‎∵ ，∴ . …… 13分 ‎∴ . ∴ .‎ ‎∴ . …… 14分