- 2021-11-11 发布 |
- 37.5 KB |
- 12页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2009年湖南省娄底市中考数学试题
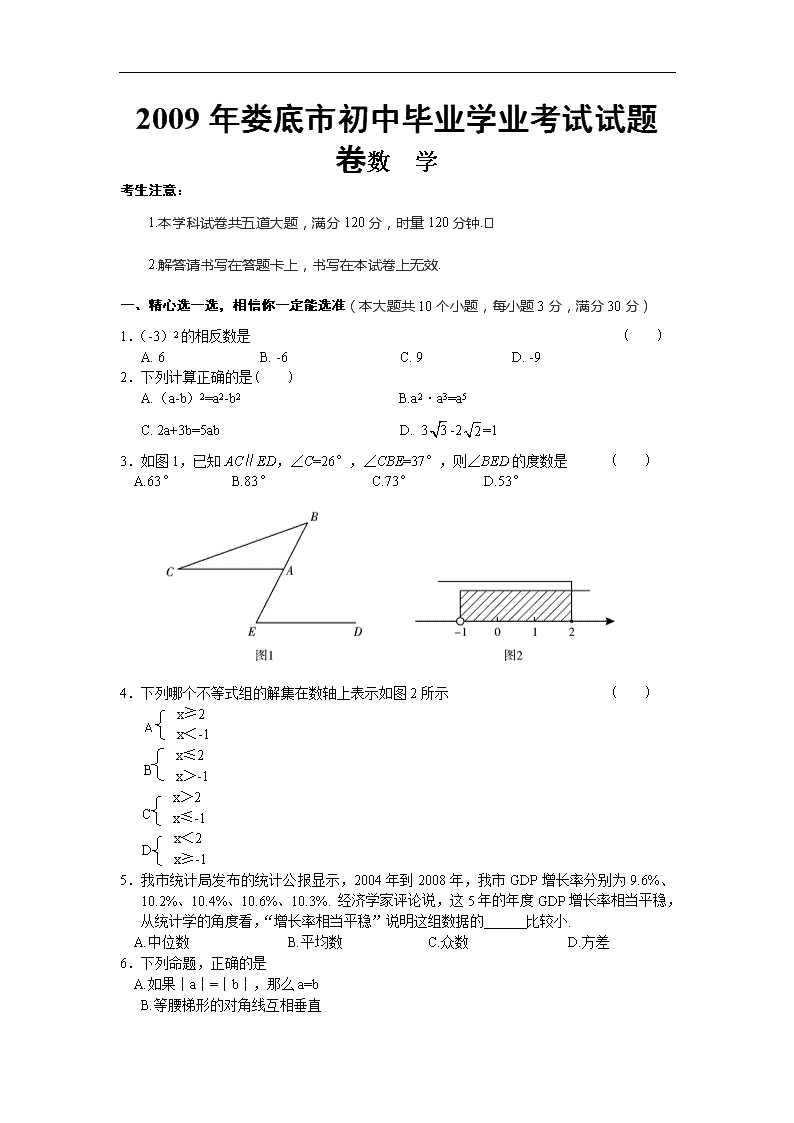
2009年娄底市初中毕业学业考试试题卷数 学 考生注意: 1.本学科试卷共五道大题,满分120分,时量120分钟. 2.解答请书写在答题卡上,书写在本试卷上无效. 一、精心选一选,相信你一定能选准(本大题共10个小题,每小题3分,满分30分) 1.(-3)2的相反数是 ( ) A. 6 B. -6 C. 9 D. -9 2.下列计算正确的是( ) A.(a-b)2=a2-b2 B.a2·a3=a5 C. 2a+3b=5ab D. 3-2=1 3.如图1,已知AC∥ED,∠C=26°,∠CBE=37°,则∠BED的度数是 ( ) A.63° B.83° C.73° D.53° 4.下列哪个不等式组的解集在数轴上表示如图2所示 ( ) A x≥2 x<-1 B x≤2 x>-1 C x>2 x≤-1 D x<2 x≥-1 5.我市统计局发布的统计公报显示,2004年到2008年,我市GDP增长率分别为9.6%、10.2%、10.4%、10.6%、10.3%. 经济学家评论说,这5年的年度GDP增长率相当平稳,从统计学的角度看,“增长率相当平稳”说明这组数据的 比较小. A.中位数 B.平均数 C.众数 D.方差 6.下列命题,正确的是 A.如果|a|=|b|,那么a=b B.等腰梯形的对角线互相垂直 C.顺次连结四边形各边中点所得到的四边形是平行四边形 D.相等的圆周角所对的弧相等 7.市一小数学课外兴趣小组的同学每人制作一个面积为200cm2的矩形学具进行展示. 设矩形的宽为xcm,长为ycm,那么这些同学所制作的矩形长y(cm)与宽x(cm)之间的函数关系的图象大致是 ( ) 8.如图3,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是 ( )A. AD=BD B.∠ACB=∠AOE C. D.OD=DE 9.小明在一次军事夏令营活动中,进行打靶训练,在用枪瞄准目标 点B时,要使眼睛O、准星A、目标B在同一条直线上,如图4 所示,在射击时,小明有轻微的抖动,致使准星A偏离到A′, 若OA=0.2米,OB=40米,AA′=0.0015米,则小明射击到的点B′ 偏离目标点B的长度BB′为 A.3米 B.0.3米 C.0.03米 D.0.2米 10. 一次函数y=kx+b与反比例函数y=kx的图象如图5所示, 则下列说法正确的是 A.它们的函数值y随着x的增大而增大 B.它们的函数值y随着x的增大而减小 C.k<0 D.它们的自变量x的取值为全体实数 二、细心填一填,你一定能填对(本大题共6个小题,每小 题3分,满分18分) 11.计算:2-1+-cos60°= . 12.下面有A、B、C、D、E五张质地均匀、大小形状完全相同的卡片,有运算式的一面朝 下,洗匀后,从中随机抽取1张卡片,卡片上运算正确的概率是 . (a2)3=a5 C 2×(-5)=-10 A a(3a-1)=3a2-a B x3·x-4=x E =1 D 13.如图6,已知AB是⊙O的直径,PB是⊙O的切线,PA 交⊙O于C,AB=3cm,PB=4cm, 则BC= . 14.为应对金融危机,拉动内需,湖南省人民政府定今年为“湖南旅游年”. 青年旅行社3 月底组织赴凤凰古城、张家界风景区旅游的价格为每人1000元,为了吸引更多的人赴 凤凰、张家界旅游,在4月底、5月底进行了两次降价,两次降价后的价格为每人810 元,那么这两次降价的平均降低率为 . 15.如图7,⊙O的半径为2,C1是函数y=x2的图象,C2是函 数y=-x2的图象,则阴影部分的面积是 . 16.王婧同学用火柴棒摆成如下的三个“中”字形图案,依此规 律,第n个“中”字形图案需 根火柴棒. 三、细心算一算,千万别出错哟(本大题共3个小题,满分22分) 17.(本小题7分)先化简,再求值: +÷,其中x=. 18.(本小题7分)娄底至新化高速公路的路基工程分段招标,市路桥公司中标承包了一段 路基工程,进入施工场地后,所挖筑路基的长度y(m)与挖筑时间x(天)之间的函 数关系如图所示,请根据提供的信息解答下列问题:(1)请你求出: ①在0≤x<2的时间段内,y与x的函数关系式; ②在x≥2时间段内,y与x的函数关系式. (2)用所求的函数解析式预测完成1620 m的路基工 程,需要挖筑多少天? 19.(本小题8分)在学习实践科学发展观的活动中,某单 位在如图8所示的办公楼迎街的墙面上垂挂一长为30 米的宣传条幅AE,张明同学站在离办公楼的地面C处 测得条幅顶端A的仰角为50°,测得条幅底端E的仰 角为30°. 问张明同学是在离该单位办公楼水平距离 多远的地方进行测量?(精确到整数米) (参考数据:sin50°≈0.77,cos50°≈0.64, tan50° ≈1.20,sin30°=0.50,cos30°≈0.87,tan30°≈ 0.58) 四、操作与应用(本大题共4个小题,满分30分) 20.(本小题6分)如图9所示,每个小方格都是边 长为1的正方形,以O点为坐标原点建 立平面直角坐标系. (1)画出四边形OABC关于y轴对称的四边形 OA1B1C1,并写出点B1的坐标是 . (2)画出四边形OABC绕点O顺时针方向旋转 90°后得到的四边形OA2B2C2,并求出点C 旋转到点C2经过的路径的长度. 21.(本小题8分)如图10,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的 延长线上取一点E,连结BE,CE. (1)求证:△ABE≌△ACE (2)当AE与AD满足什么数量关系时,四边形ABEC是 菱形?并说明理由. 22.(本小题8分)为了加快社会主义新农村建设,让农民享受改革开放30年取得的成果, 党中央、国务院决定:凡农民购买家电和摩托车享受政府13%的补贴(凭购物发票到 乡镇财政所按13%领取补贴). 星星村李伯伯家今年购买了一台彩电和一辆摩托车共花 去6000元,且该辆摩托车的单价比所买彩电的单价的2倍还多600元. (1)李伯伯可以到乡财政所领到的补贴是多少元? (2)求李伯伯家所买的摩托车与彩电的单价各是多少元? 23.(本小题8分)“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做些力 所能及的家务. 王刚同学在本学期开学初对部分同学寒假在家做家务的时间进行了抽 样调查(时间取整数小时),所得数据统计如下表: 时间分组 0.5~20.5 20.5~40.5 40.5~60.5 60.5~80.5 80.5~100.5 频 数 20 25 30 15 10 (1)抽取样本的容量是 . (2)根据表中数据补全图中的频数分布直方 图. (3)样本的中位数所在时间段的范围是 . (4)若该学校有学生1260人,那么大约有多 少学生在寒假做家务的时间在40.5~100.5 小时之间? 五、综合与探究(本大题共2个小题,满分20分) 24.(本小题8分)已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4. (1)探究m满足什么条件时,二次函数y的图象与x轴的交点的个数. (2)设二次函数y的图象与x轴的交点为A(x1,0),B(x2,0),且+=5,与y轴的交点为C,它的顶点为M,求直线CM的解析式. 25.(本小题12分)如图11,在△ABC中,∠C=90°,BC=8,AC=6,另有一直角梯形DEFH (HF∥DE,∠HDE=90°)的底边DE落在CB上,腰DH落在CA上,且DE=4,∠DEF=∠CBA,AH∶AC=2∶3 (1)延长HF交AB于G,求△AHG的面积. (2)操作:固定△ABC,将直角梯形DEFH以每秒1个 单位的速度沿CB方向向右移动,直到点D与点B 重合时停止,设运动的时间为t秒,运动后的直角梯 形为DEFH′(如图12). 探究1:在运动中,四边形CDH′H能否为正方形?若能, 请求出此时t的值;若不能,请说明理由. 探究2:在运动过程中,△ABC与直角梯形DEFH′重叠 部分的面积为y,求y与t的函数关系. 2009年娄底市初中毕业学业考试试题卷 数学参考答案及评分标准 一、精心选一选,相信你一定能选准(本大题共10个小题,每小题3分,满分30分) 题 号 1 2 3 4 5 6 7 8 9 10 答 案 D B A B D C A D B C 二、细心填一填,你一定能填对(本大题共6个小题,每小题3分,满分18分) 11.1 12. 13. 14.10% 15.2π 16.6n+3或9+6(n-1) 三、细心算一算,千万别出错哟(本大题共3个小题,满分22分) 17.(7分) 解:原式=+×……………………………………1分 =+………………………………………………2分 =+ =……………………………………………………3分 =………………………………………………………………4分 =…………………………………………………………………5分 当x=时,原式=………………………………6分 =1-……………………………………7分 18.(7分) 解:(1)当0≤x<2时,设y与x的函数关系式为y=kx……………………………1分 ∴40=k ∴y与x的函数式为y=40x(0≤x<2)………………………………………2分 (2)当x≥2时,设y与x的函数式为y=kx+b………………………………3分 ………………………………………………(4分) 115=3k+b 255=7k+b 解之得 k=35 b=10 ∴y与x的函数式为y=35x+10(x≥2)……………………………………5分 (3)当y=1620时,35x+10=1620 x=46…………………………………………………………………………6分 答:需要挖筑46天.…………………………………………………………7分 19.(8分) 解:方法一:过D点作DF⊥AB于F点………………………………………………1分 在Rt△DEF中,设EF=x,则DF=x…………………………………………………2分在Rt△ADF中,tan50°=≈1.204分 30+x=x×1.20 x≈27.8…………………………………………………6分 ∴DF=x≈48…………………………………………7分 答:张明同学站在离办公楼约48米处进行测量的.………………………………8分 方法二:过点D作DF⊥AB于F点………………………………………………1分 在Rt△DEF中,EF=FD·tan30°……………………………………………………3分 在Rt△AFD中,AF=FD·tan30°……………………………………………………5分 ∵AE+EF=AF ∴30+FDtan30°=FD·tan50°………………………………………………………6分 ∴FD≈48………………………………………………………………………………7分 答:张明同学站在离办公楼约48米处进行测量的.………………………………8分 (其他方法参照给分) 四、操作与应用(本大题共4个小题,满分30分) 20.(6分) 解:(1)如图:B1的坐标是(-6,2) (作图2分,填空1分,共3分) (2)如图: L==π (作图2分,计算1分,共3分) 21.(8分) (1)证明:∵AB=AC 点D为BC的中点 ∴∠BAE=∠CAE…………………………………………………………2分 AE=AE ∴△ABE≌△ACE(SAS)………………………………………………4分 (2)当AE=2AD(或AD=DE或DE=AE)时,四边形ABEC是菱形…………6分 理由如下: ∵AE=2AD,∴AD=DE 又点D为BC中点,∴BD=CD ∴四边形ABEC为平行四形边……………………………………………………7分 ∵AB=AC ∴四边形ABEC为菱形………………………………………………………………8分 (其他方法参照本方法给分) 22.(8分) 解:(1)6000×13%=780……………………………………………………1分 答:李伯伯可以从政府领到补贴780元………………………………2分 (2)方法一:设彩电的单价为x元/台……………………………………3分 x+2x+600=6000…………………………………………………………5分 3x=5400 x=1800……………………………………………………………………6分 2x+600=2×1800+600=4200………………………………………………7分 答:彩电与摩托车的单价分别为1800元/台、4200元/辆……………………8分 方法二:设买摩托车的单价为x元/辆,彩电单价为y元/台………………3分 ……………………………5分 x+y=6000 x=2y+600 ……………………………7分 解之得 x=4200 y=18007 答:彩电与摩托车的单价分别为1800元/台、4200元/辆………………8分 23.(8分) 解:(1)100……………………2分 (2)如图……………………4分 (3)40.5~60.5………………6分 (4)×1260=693……7分 答:大约有693名学生在寒假做家务的时间在40.5~100.5小时之间.……8分 五、综合与探究(本大题共2个小题,满分20分) 24.(8分) 解:(1)令y=0,得:x2-(2m-1)x+m2+3m+4=0 △=(2m-1)2-4(m2+3m+4)=-16m-15…………………………1分 当△>0时,方程有两个不相等的实数根,即-16m-15>0 ∴m<- 此时,y的图象与x轴有两个交点………………………………2分 当△=0时,方程有两个相等的实数根,即-16m-15=0 ∴m=- 此时,y的图象与x轴只有一个交点………………………………3分 当△<0时,方程没有实数根,即-16m-15<0 ∴m>- 此时,y的图象与x轴没有交点 ∴当m<-时,y的图象与x轴有两个交点; 当m=-时,y的图象与x轴只有一个交点; 当m>-时,y的图象与x轴没有交点.……………………4分 (评分时,考生未作结论不扣分) (2)由根与系数的关系得x1+x2=2m-1,x1x2=m2+3m+4………………5分 +=(x1+x2)2-2x1x2=(2m-1)2-2(m2+3m+4)=2m2-10m-7……6分 ∵+=5,∴2m2-10m-7=5,∴m2-5m-6=0 解得:m1=6,m2=-1 ∵m<-,∴m=-1 ∴y=x2+3x+2……………………………………………………………………7分 令x=0,得y=2,∴二次函数y的图象与y轴的交点C坐标为(0,2) 又y=x2+3x+2=(x+)2-,∴顶点M的坐标为(-,-) 设过C(0,2)与M(-,-)的直线解析式为y=kx+b 解得 则2=b k= -=k+b,b=2 ∴所求的解析式为y=x+2…………………………………………8分 25.(12分) 解:(1)∵AH∶AC=2∶3,AC=6 ∴AH=AC=×6=4 又∵HF∥DE,∴HG∥CB,∴△AHG∽△ACB…………………………1分 ∴=,即=,∴HG=…………………………………2分 ∴S△AHG=AH·HG=×4×=……………………………………3分 (2)①能为正方形…………………………………………………………………4分 ∵HH′∥CD,HC∥H′D,∴四边形CDH′H为平行四边形 又∠C=90°,∴四边形CDH′H为矩形…………………………………5分 又CH=AC-AH=6-4=2 ∴当CD=CH=2时,四边形CDH′H为正方形 此时可得t=2秒时,四边形CDH′H为正方形…………………………6分 ②(Ⅰ)∵∠DEF=∠ABC,∴EF∥AB ∴当t=4秒时,直角梯形的腰EF与BA重合. 当0≤t≤4时,重叠部分的面积为直角梯形DEFH′的面积.…………7分 过F作FM⊥DE于M,=tan∠DEF=tan∠ABC=== ∴ME=FM=×2=,HF=DM=DE-ME=4-= ∴直角梯形DEFH′的面积为(4+)×2= ∴y=………………………………………………………………8分 (Ⅱ)∵当4<t≤5时,重叠部分的面积为四边形CBGH的面积-矩形CDH′H的面积.…………………………………………………………9分 而S边形CBGH=S△ABC-S△AHG=×8×6-= S矩形CDH′H=2t ∴y=-2t……………………………………………………………………10分 (Ⅲ)当5<t≤8时,如图,设H′D交AB 于P. BD=8-t 又=tan∠ABC= ∴PD=DB=(8-t)………………11分 ∴重叠部分的面积y=S △PDB=PD·DB =·(8-t)(8-t) =(8-t)2=t2-6t+24 ∴重叠部分面积y与t的函数关系式: ……………………………………12分 y=(0≤t≤4) -2t(4<t≤5) t2-6t+24(5<t≤8) (注:评分时,考生未作结论不扣分)查看更多