- 2021-11-11 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019九年级数学上册 第六章 反比例函数 2 反比例函数的图象与性质(1)教案 (新版)北师大版
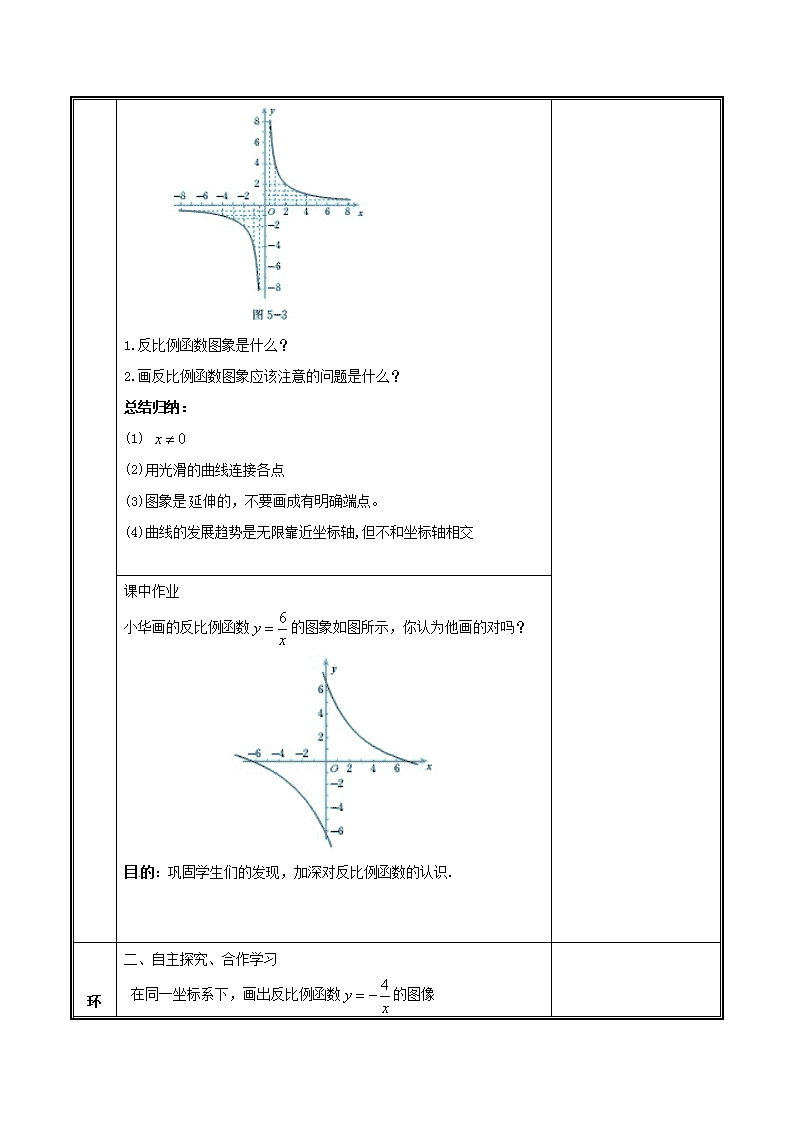
反比例函数的图像和性质 课 题 反比例函数的图像和性质 课时安排 共(2 )课时 课程标准 课标P34 能画出反比例函数的图像,根据图像和表达式探索理解k>0和k<0时,图像的变化情况 学习目标 1.通过学生自己动手列表、描点、连线,进一步熟悉作函数图象的主要步骤,会作反比例函数的图象. 2.通过观察图象,概括反比例函数的有关性质,逐步提高从函数图象中获取信息的能力. 3.能利用反比例函数的性质进行简单的应用. 教学重点 目标1,2 教学难点 目标2.3 教学方法 引导发现法、讨论法. 教学准备 PPT,几何画板 课前作业 复习反比例函数的定义,会准确判断反比例函数。 教学过程 教学环节 课堂合作交流 二次备课 (修改人: ) 环 节 一 一、设疑激思 复习引入 教师幻灯片展示下列问题: 1.当初我们从哪些方面研究了一次函数? 2.画一次函数图象的步骤是什么? 3.借助图象我们研究了一次函数的哪些性质? 二、合作探究 发现问题 教师引导学生类比着画一次函数图象的过程来尝试画出反比例函数的图象. 小组内交流:教师在巡视过程中,当发现大部分学生完成时,让同学们先在小组内进行互查、互批,让小组长汇总各小组出现的问题或不足; 全班交流:小组代表发言,谈一下各小组内在画图过程中存在哪些问题,教师组织、指导学生对各组情况和问题进行汇总。 让学生通过刚才两个过程中积累的知识和经验,对小亮的作法进行点评。 小明的做法: x -8 -4 -3 -2 -1 - 1 2 3 4 8 y= - -1 - -2 -4 -8 8 4 2 1 (1)列表: (2)描点: (图5-1) (3)连线:(图5-2) 学生回答:小明的画法不正确,不是用光滑的曲线顺次连接各点;图象不是无限延伸的. 教师再结合以上几个环节,进行总的总结和点评 教师用幻灯片展示正确的反比例函数图象(图5-3): 1.反比例函数图象是什么? 2.画反比例函数图象应该注意的问题是什么? 总结归纳: (1) (2)用光滑的曲线连接各点 (3)图象是延伸的,不要画成有明确端点。 (4)曲线的发展趋势是无限靠近坐标轴,但不和坐标轴相交 课中作业 小华画的反比例函数的图象如图所示,你认为他画的对吗? 目的:巩固学生们的发现,加深对反比例函数的认识. 环 二、自主探究、合作学习 在同一坐标系下,画出反比例函数的图像 节 二 让学生巩固作反比例函数图象的步骤,并且初步感受反比例函数图象的特征。 课中作业 观察和的图象的形状和位置,有什么相同点和不同点。(图象见课件) 1.自己观察图象找出相同点和不同点。 2.小组展开讨论反比例函数和的图象在哪两个象限,由什么确定。 3.引导总结。 环 节 三 三、拓展应用,学科互联 用几何画板验证猜想 得出结论: 图象分别都是由两支曲线组成,因此称反比例函数的图象为双曲线. 反比例函数的图象由k决定. 当k>0时,两支双曲线分别位于一,三象限内; 当k<0时,两支双曲线分别位于二,四象限内. 四、感悟收获,师生小结 通过本节课的学习,你有哪些收获?你还存在什么疑问? 课中作业 活学活用 巩固提高 1.已知y= (k≠0)的图象的一部分如图,则k__________0 2. 反比例函数的图象两支分布在第二、四象限,则点(, )在 ( ) A 第一象限 B 第二象限 C 第三象限 D 第四象限 课后作业设计: 《全品学练考》作业手册 习题6.2 (修改人: ) 板书设计: 反比例函数的图像与性质 一、反比例函数的定义 形如 二、 反比例函数的图像和性质: k>0 k<0 图像形状 两支双曲线 两支双曲线 图像位置 一、三象限(内) 二、四象限(内) 对称性 关于直线成轴对称 关于原点成中心对称 关于直线成轴对称 关于原点成中心对称 教学反思: 学生已经学习过一次函数,对研究函数的图象和性质的思想方法已有所了解,在此基础上探索反比例函数的图象和性质,学生通过类比的方法学习,实现知识的迁移,可以学得比较轻松,同时也会对二次函数和高中阶段各种函数的学习产生积极的影响。所以要加强引导学生的自主学习,培养学生自主探索,终身学习的意识。在本节课中,学生通过列表、描点、连线画出有别于一次函数图象的双曲线,以及由反比例函数的图象归纳总结出反比例函数的性质会有一定的挑战性,但同时也为学生进行探究学习和合作学习提供了思维活动空间。 由于学生认知水平,学习能力以及学好函数的信心等方面存在差异,所以探讨活动的效果也会因人而异。这一点我们应该尊重学生的个体差异,尽可能让每个学生都学有所获。 查看更多