初中数学中考复习课件章节考点专题突破：第五章 图形性质1-22 平行四边形

初中数学中考复习课件章节考点专题突破：第五章 图形性质1-22 平行四边形

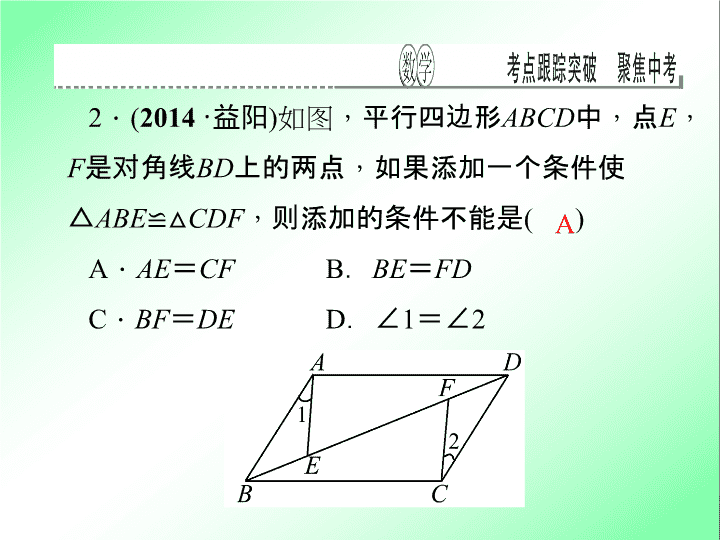
考点跟踪突破 22 　平行四边形 一、选择题 ( 每小题 6 分 ， 共 30 分 ) 1 ． ( 2014 · 衡阳 ) 若一个多边形的内角和是 900° ， 则这个多边形的边数为 ( ) A ． 五 B ．六 C ．七 D ．八 C 2 ． ( 2014 · 益阳 ) 如图， 平行四边形 ABCD 中 ， 点 E ， F 是对角线 BD 上的两点 ， 如果添加一个条件使 △ ABE ≌△ CDF ， 则添加的条件不能是 ( ) A ． AE ＝ CF B ． BE ＝ FD C ． BF ＝ DE D ． ∠ 1 ＝ ∠ 2 A 3 ． ( 2014 · 长沙 ) 平行四边形的对角线一定具有的性质是 ( ) A ． 相等 B ．互相平分 C ． 互相垂直 D ．互相垂直且相等 B 4 ． ( 2014· 枣庄 ) 如图 ， △ ABC 中 ， AB ＝ 4 ， AC ＝ 3 ， AD ， AE 分别是其角平分线和中线 ， 过点 C 作 CG ⊥ AD 于点 F ， 交 AB 于点 G ， 连接 EF ， 则线段 EF 的长为 ( ) A . 1 2 B ． 1 C . 7 2 D ． 7 A 5 ． 在面积为 15 的平行四边形 ABCD 中 ， 过点 A 作 AE ⊥ 直线 BC 于点 E ， 作 AF ⊥ 直线 CD 于点 F ， 若 AB ＝ 5 ， BC ＝ 6 ， 则 CE ＋ CF 的值为 ( ) A ． 11 ＋ 11 3 2 B ． 11 － 11 3 2 C ． 11 ＋ 11 3 2 或 11 － 11 3 2 D ． 11 ＋ 11 3 2 或 1 ＋ 3 2 C 二、填空题 ( 每小题 6 分 ， 共 30 分 ) 6 ． ( 2014 · 梅州 ) 内角和与外角和相等的多边形的边数为 ____ ． 7 ． ( 2013 · 滨州 ) 在 ▱ ABCD 中 ， 点 O 是对角线 AC ， BD 的交点 ， 点 E 是边 CD 的中点 ， 且 AB ＝ 6 ， BC ＝ 10 ， 则 OE ＝ ____ ． 四 5 8 ． ( 2013 · 江西 ) 如图 ， ▱ ABCD 与 ▱ DCFE 的周长相等 ， 且 ∠ BAD ＝ 60° ， ∠ F ＝ 110° ， 则 ∠ DAE 的度数为 ． 25° 9 ． ( 2014· 福州 ) 如图 ， 在 Rt △ ABC 中 ， ∠ ACB ＝ 90 ° ， 点 D ， E 分别是边 AB ， AC 的中点 ， 延长 BC 到点 F ， 使 CF ＝ 1 2 BC. 若 AB ＝ 10 ， 则 EF 的长是 __ __ ． 5 10 ． ( 2014· 襄阳 ) 在 ? ABCD 中 ， BC 边上的高为 4 ， AB ＝ 5 ， AC ＝ 2 5 ， 则 ? ABCD 的周长等于 __ __ ． 12 或 20 三、解答题 ( 共 40 分 ) 11 ． (10 分 ) ( 2013 · 泸州 ) 如图 ， 已知 ▱ ABCD 中 ， F 是 BC 边的中点 ， 连接 DF 并延长 ， 交 AB 的延长线于点 E. 求证： AB ＝ BE. 解：证明： ∵ F 是 BC 边的中点 ， ∴ BF ＝ CF ， ∵ 四边形 ABCD 是平行四边形 ， ∴ AB ＝ DC ， AB ∥ CD ， ∴∠ C ＝ ∠ FBE ， ∠ CDF ＝ ∠ E ， ∵ 在 △ CDF 和 △ BEF 中 î ï í ï ì ∠ C ＝ ∠ FBE ， ∠ CDF ＝ ∠ E ， CF ＝ BF ， ∴△ CDF ≌△ BEF ( AAS ) ， ∴ BE ＝ DC ， ∵ AB ＝ DC ， ∴ AB ＝ BE 12 ． (10 分 ) ( 2014 · 凉山州 ) 如图 ， 分别以 Rt △ ABC 的直角边 AC 及斜边 AB 向外作等边 △ ACD ， 等边 △ ABE. 已知 ∠ BAC ＝ 30° ， EF ⊥ AB ， 垂足为点 F ， 连接 DF. (1) 试说明 AC ＝ EF ； (2) 求证：四边形 ADFE 是平行四边形． ∵△ ACD 是等边三角形 ， ∴∠ DAC ＝ 60° ， AC ＝ AD ， ∴∠ DAB ＝ ∠ DAC ＋ ∠ BAC ＝ 90° ， ∴ EF ∥ AD ， ∵ AC ＝ EF ， AC ＝ AD ， ∴ EF ＝ AD ， ∴ 四边形 ADFE 是平行四边形 13 ． (10 分 ) ( 2012 · 孝感 ) 我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形．如图 ， 在四边形 ABCD 中 ， 点 E ， F ， G ， H 分别是边 AB ， BC ， CD ， DA 的中点 ， 依次连接各边中点得到的中点四边形 EFGH. (1) 这个中点四边形 EFGH 的形状是 ； 平行四边形 (2) 请证明你的结论． 14 ． (10 分 ) ( 2013 · 莱芜 ) 如图 ， 在 Rt △ ABC 中 ， ∠ C ＝ 90° ， 以 AC 为一边向外作等边三角形 ACD ， 点 E 为 AB 的中点 ， 连接 DE. (1) 证明： DE ∥ CB ； (2) 探索 AC 与 AB 满足怎样的数量关系时 ， 四边形 DCBE 是平行四边形．