2012年四川省南充市高中阶段学校招生统一考试数学试卷（含答案）

2012年四川省南充市高中阶段学校招生统一考试数学试卷（含答案）

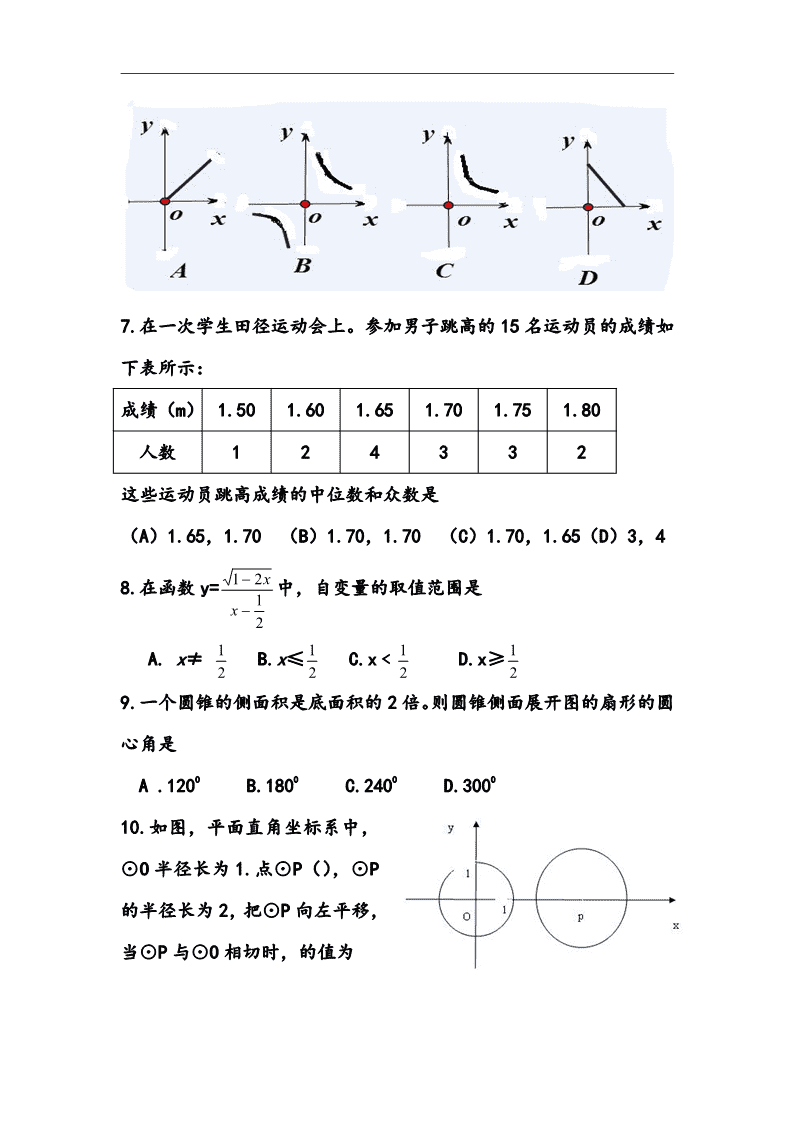
南充市二 O 一二年高中阶段学校招生统一考试 数 学 试 卷 （满分 100 分，时间 90 分钟） 一、选择题（本大题共 10 个小题，每小题 3 分，共 30 分） 每小题都有代号为 A、B、C、D 四个答案选项，其中只有一个是正确的，请把 正确选项的代号填在相应的括号内．填写正确记 3 分，不填、填错或填出的代号 超过一个记 0 分． 1．计算 2－（－3）的结果是（ ）． （A）5 （B）1 （C）－1 （D）－5 2.下列计算正确的是（ ） （A）x3+ x3=x6 （B）m2·m3=m6 （C）3 2 - 2 =3 （D） 14 × 7 =7 2 3.下列几何体中，俯视图相同的是（ ）． （A）①② （B）①③ （C）②③ （D）②④ ① ② ③ ④ 4.下列函数中是正比例函数的是 （ ） （ A ）y=-8x （B）y= x 8 （ C ）y=5x2+6 （D）y= -0.5x-1 5.方程 x（x-2）+x-2=0 的解是（ ） （A）2 （B）-2,1 （C）－1 （D）2,－1 6.矩形的长为 x，宽为 y，面积为 9，则 y 与 x 之间的函数关系用图 像表示大致为（ ） 7.在一次学生田径运动会上。参加男子跳高的 15 名运动员的成绩如 下表所示： 成绩（m） 1.50 1.60 1.65 1.70 1.75 1.80 人数 1 2 4 3 3 2 这些运动员跳高成绩的中位数和众数是 （A）1.65，1.70 （B）1.70，1.70 （C）1.70，1.65（D）3，4 8.在函数 y= 2 1 21   x x 中，自变量的取值范围是 A. x≠ 2 1 B.x≤ 2 1 C.x﹤ 2 1 D.x≥ 2 1 9.一个圆锥的侧面积是底面积的 2 倍。则圆锥侧面展开图的扇形的圆 心角是 A .1200 B.1800 C.2400 D.3000 10.如图，平面直角坐标系中， ⊙O 半径长为 1.点⊙P（），⊙P 的半径长为 2，把⊙P 向左平移， 当⊙P 与⊙O 相切时，的值为 （A）3 （B）1 （C）1，3 （D）±1，±3 二、填空题（本大题共 4 个小题，每小题 3 分，共 12 分）请将答案直接填写在题中横 线上． 11.不等式 x+2＞6 的解集为 12.分解因式 x2-4x-12= 13.如图，把一个圆形转盘按 1﹕2﹕3﹕4 的比例分成 A、B、C、D 四 个扇形区域，自由转动转盘，停止后指针落在 B 区域的概率为 14. 如图，四边形 ABCD 中，∠BAD=∠BCD=900,AB=AD,若四边形 ABCD 的面积是 24cm2.则 AC 长是 cm. 三、（本大题共 3 个小题，每小题 6 分，共 18 分） 15.计算： 1a a + 12 1   a a 16.在一个口袋中有 4 个完全相同的小球，把它们分别标号为 1、2、 3、4，随机地摸取一个小球然后放回，再随机地摸出一个小球，求下 列事件的概率： (1)两次取的小球的标号相同 （2）两次取的小球的标号的和等于 4 17.如图，等腰梯形 ABCD 中，AD∥BC，点 E 是 AD 延长线上的一点， 且 CE=CD，求证：∠B=∠E 四、（本大题共 2 个小题，每小题 8 分，共 16 分） 18.关于 x 的一元二次方程 x2+3x+m-1=0 的两个实数根分别为 x1,x2． （1）求 m 的取值范围． （2）若 2（x1+x2）+ x1x2+10=0．求 m 的值. 19.矩形 ABCD 中，AB=2AD，E 为 AD 的中点，EF⊥EC 交 AB 于点 F,连 接 FC. (1)求证：⊿AEF∽⊿DCE (2)求 tan∠ECF 的值. 五、（本题满分 8 分） 20.学校 6 名教师和 234 名学生集体外出活动，准备租用 445 座大客 车或 30 座小客车，若租用 1 辆大车 2 辆小车供需租车费 1000 元；若 若租用 2 辆大车 1 辆小车供需租车费 1100 元. （1）求大、小车每辆的租车费各是多少元？ （2）若每辆车上至少．．要有一名教师，且总租车费用不超过．．．2300 元， 求最省钱的租车方案。 六、（本题满分 8 分） 21.在 Rt⊿POQ 中，OP=OQ=4,M 是 PQ 中点，把一三角尺的直角顶点放 在点 M 处，以 M 为旋转中心，旋转三角尺，三角尺的两直角边与⊿POQ 的两直角边分别交于点 A、B， (1)求证：MA=MB (2)连接 AB，探究：在旋转三角尺的过程中，⊿AOB 的周长是否存在 最小值，若存在，求出最小值，若不存在。请说明理由。 七、（本题满分 8 分） 22.如图，⊙C的内接⊿AOB中，AB=AO=4,tan∠AOB= 4 3 ,抛物线y=ax2+bx 经过点 A(4，0)与点（-2，6） （1）求抛物线的函数解析式． （2）直线 m 与⊙C 相切于点 A 交 y 轴于点 D，动点 P 在线段 OB 上， 从点 O 出发向点 B 运动;同时动点 Q 在线段 DA 上，从点 D 出发向点 A 运动，点 P 的速度为每秒 1 个单位长，点 Q 的速度为每秒 2 个单位长， 当 PQ⊥AD 时,求运动时间 t 的值 （3）点 R 在抛物线位于 x 轴下方部分的图象上，当⊿ROB 面积最大 时，求点 R 的坐标. 数学试题参考答案及评分意见 一、选择题（本大题共 10 个小题，每小题 3 分，共 30 分 题号 1 2 3 4 5 6 7 8 9 10 答案 A D C A D C C C B D 二、填空题（本大题共 4 个小题，每小题 3 分，共 12 分） 11. x＞4 12. (x-6)(x+2)； 13. 0.2 14. 4 3 ． 三、（本大题共 3 个小题，每小题 6 分，共 18 分） 15. 解：原式＝ 1a a + )1)(1( 1   aa a ……（2 分） ＝ 1a a + 1 1 a ……（4 分） ＝ 1 1   a a …（5 分） ＝1． …（6 分） 16. 解 ： 画 出 树 状 图 为： 由图可知共有 16 种等 可能的结果，其中两 次取得小球队标号相 同有 4 种（记为 A），标号的和等于 4 的有 3 种（记为 B） ∴P（A）= 16 4 = 4 1 ……（4 分） P（B）= 16 3 …（6 分） 17. 证明：∵ABCD 是等腰梯形，AD∥BC ∴∠B=∠BCD, ∠EDC=∠E ∴CE=CD∴∠EDC=∠E∴∠B=∠E 解四、（本大题共 2 个小题，每小题 8 分，共 16 分） 18 解：（1）∵关于 x 的一元二次方程 x2+3x+m-1=0 的两个实数根分别 为 x1,x2． ∴ ⊿≥0． 即 32-4（m-1）≥0，解得,m≤ 4 13 ． ……（4 分） （2）由已知可得 x1+x2=3 x1x2 = m-1 又 2（x1+x2）+ x1x2+10=0 ∴2×（-3）+m-1+10=0 ……（6 分） ∴m=-3……（8 分） 19.（1）证明：∵ABCD 是矩形 ∴∠A=∠D=900 ∴∠DCE+∠DEC=900 ∵EF⊥EC ∴∠AEF+∠DEC=900 ∴∠DCE=∠AEF ∴⊿AEF∽⊿DCE (2)由（1）可知：⊿AEF∽⊿DCE ∴ DC AE = CE EF 在矩形 ABCD 中，E 为 AD 的中点。 AB=2AD ∴ DC=AB=4AE ∴ tan∠ECF= CE EF = DC AE = AE AE 4 = 4 1 五、 （本题满分 8 分） 20 解：(1)设大、小车每辆的租车费各是 x、y 元 则 x+2y=1000 x=400 2x+y=1100 解得： y=300 答：大、小车每辆的租车费各是 400 元、300 元 （2）240 名师生都有座位，租车总辆数≥6；每辆车上至少要有一名 教师，租车总辆数≤6.故租车总数事故 6 辆，设大车辆数是 x 辆，则 租小车（6-x）辆 45x+30(6-x) ≥240 x≥4 400x+300(6-x)≤2300 解得： x≤5 ∴ 4≤x≤5 ∵x 是正整数 ∴ x=4 或 5 于是又两种租车方案，方案 1：大车 4 辆 小车 2 辆 总租车费用 2200 元，方案 2：大车 5 辆 小车 1 辆 总租车费用 2300 元，可见最省钱 的是方案 1 六、（本题满分 8 分） 21（1）证明：连接 OM ∵ Rt⊿POQ 中，OP=OQ =4,M 是 PQ 的中点 ∴OM=PM= 2 1 PQ=2 2 ∠POM=∠BOM=∠P=450 ∵∠PMA+∠AMO=∠OMB+∠AMO ∴∠PMA=∠OMB ⊿PMA≌⊿OMB ∴ MA=MB (2)解：⊿AOB 的周长存在最小值 理由是: ⊿PMA≌⊿OMB ∴ PA=OB ∴OA+OB=OA+PA=OP=4 令 OA=x AB=y 则 y2=x2+(4-x)2=2x2-8x+16 =2(x-2)2+8≥8 当 x=2 时 y2 有最小值=8 从而 y≥2 2 故⊿AOB 的周长存在最小值，其最小值是 4+2 2 七、（本题满分 8 分） 22 解：（1）把点 A(4，0)与点（-2，6）代入抛物线 y=ax2+bx，得： 16a+4b=0 a= 2 1 4a-2b=6 解得： b= -2 ∴抛物线的函数解析式为：y= 2 1 x2-2x （2）连 AC 交 OB 于 E ∵直线 m 切⊙C 于 A ∴AC⊥m，∵ 弦 AB=AO ∴ ⌒ AB= ⌒ AO ∴AC⊥OB ∴m∥OB ∴∠ OAD=∠AOB ∵OA=4 tan∠AOB= 4 3 ∴OD=OA·tan∠OAD=4× 4 3 =3 作 OF⊥AD 于 F OF=OA·sin∠OAD=4× 5 3 =2.4 t 秒时，OP=t,DQ=2t,若 PQ⊥AD 则 FQ=OP= t DF=DQ-FQ= t ⊿ODF 中，t=DF= 22 OFOD  =1.8 秒 （3）令 R(x, 2 1x2-2x) (0＜x＜4) 作 RG⊥y 轴于 G 作 RH⊥OB 于 H 交 y 轴于 I 则 RG= x OG= 2 1x2+2x Rt⊿RIG 中，∵∠GIR=∠AOB ∴tan∠GIR= 4 3 ∴IG= 3 4 x IR= 3 5 x, Rt⊿OIH 中， OI=IG-OG= 3 4 x-（ 2 1x2+2x）= 2 1x2- 3 2 x HI= 5 4 （ 2 1x2- 3 2 x） 于是 RH=IR-IH= 3 5 x- 5 4 （ 2 1x2- 3 2 x） =- 5 2 x2+ 15 33 x=- 5 2 x2+ 5 11x=- 5 2 ( x- 4 11)2+ 40 121 当 x= 4 11时，RH 最大。S⊿ROB 最大。这时 2 1 x2-2x= 2 1 ×( 4 11)2-2× 4 11=- 32 55 ∴点 R( 4 11,- 32 55 )