寒假课程 【精品讲义】人教版 九年级 数学 总复习 第三讲 相似和四边形（教师版）

寒假课程 【精品讲义】人教版 九年级 数学 总复习 第三讲 相似和四边形（教师版）

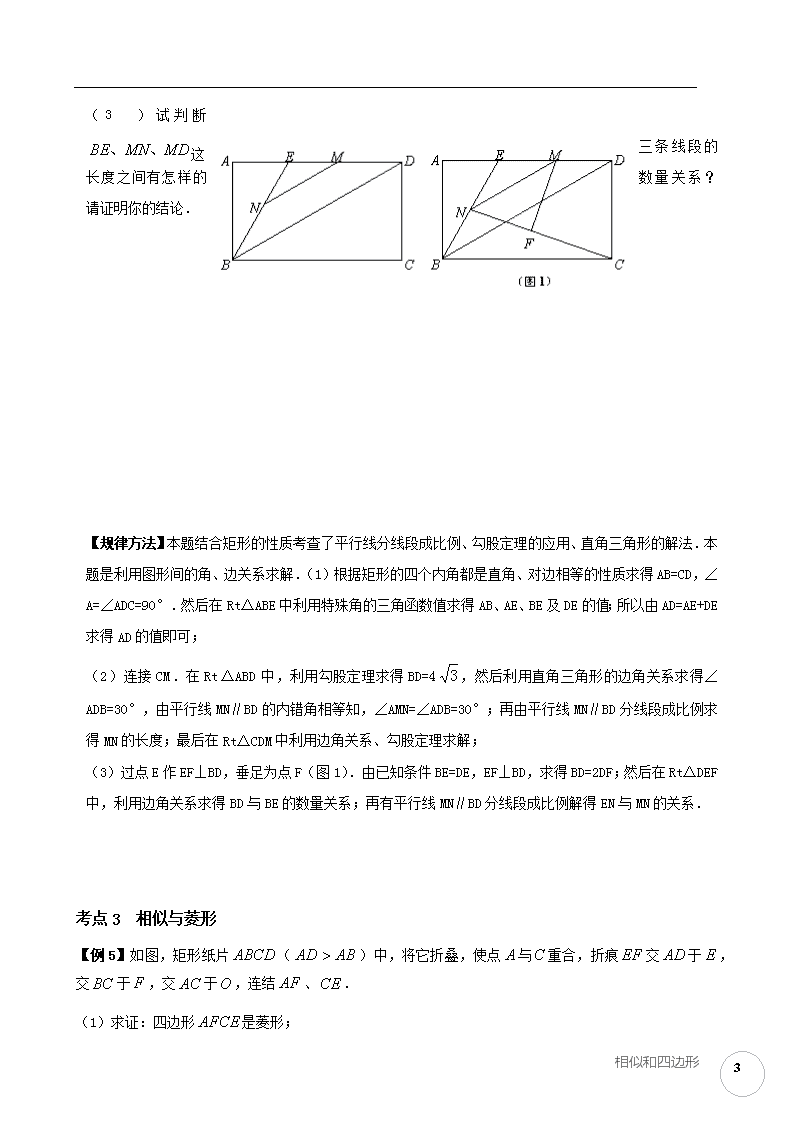
第三讲相似和四边形明确目标﹒定位考点相似三角形与四边形的考查形式是一道选择题（3分），解答题通常会与一般四边形或者特殊的四边形相结合起来考查，往往分值范围在10-14分之间。热点聚焦﹒考点突破考点1相似与平行四边形【例1】如图6，在ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=，则ΔCEF的周长为（）A.8B.9.5C.10D.11.5【规律方法】题意在综合考查平行四边形、相似三角形、和勾股定理等知识的掌握程度和灵活运用能力，同时也体现了对数学中的数形结合思想的考查．【例2】已知，如图，F为平行四边形ABCD边DC延长线上一点，连结AF，交BC于G，交BD于E，试说明=EG·EFABCFGED33相似和四边形 【规律方法】通过证明三角形相似得到线段间的相似比，再通过中间的线段比搭桥过渡即可。考点2相似与矩形【例3】已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？【规律方法】当文字叙述的两个三角形相似时，往往要分类讨论。【例4】（2014年广东华侨中学,24,14分）如图，在矩形中，点在边上，联结，，，联结．点为线段上的任意一点，过点作，与相交于点．（1）如果，求边的长；（2）如图，在（1）的条件下，如果点为线段的中点，联结．过点作，垂足为点，求线段的长；33相似和四边形 （3）试判断这三条线段的长度之间有怎样的数量关系？请证明你的结论．【规律方法】本题结合矩形的性质考查了平行线分线段成比例、勾股定理的应用、直角三角形的解法．本题是利用图形间的角、边关系求解．（1）根据矩形的四个内角都是直角、对边相等的性质求得AB=CD，∠A=∠ADC=90°．然后在Rt△ABE中利用特殊角的三角函数值求得AB、AE、BE及DE的值；所以由AD=AE+DE求得AD的值即可；（2）连接CM．在Rt△ABD中，利用勾股定理求得BD=4，然后利用直角三角形的边角关系求得∠ADB=30°，由平行线MN∥BD的内错角相等知，∠AMN=∠ADB=30°；再由平行线MN∥BD分线段成比例求得MN的长度；最后在Rt△CDM中利用边角关系、勾股定理求解；（3）过点E作EF⊥BD，垂足为点F（图1）．由已知条件BE=DE，EF⊥BD，求得BD=2DF；然后在Rt△DEF中，利用边角关系求得BD与BE的数量关系；再有平行线MN∥BD分线段成比例解得EN与MN的关系．考点3相似与菱形【例5】如图，矩形纸片（）中，将它折叠，使点与重合，折痕交于，交于，交于，连结、．（1）求证：四边形是菱形；33相似和四边形 （2）过作交于，求证：；AEDCFBPO（3）若，的面积为，求的值．（第5题图）【规律方法】本题考查了菱形的判定和性质、勾股定理、矩形的性质以及相似三角形的判定和性质的综合运用．考点4相似与正方形【例6】如图，正方形DEMF内接于△ABC，若，，求33相似和四边形 【规律方法】首先利用正方形的面积求出其边长，过A点作AQ⊥BC于Q，交DE于P，利用可得AP及AQ的长，再由△ADE∽△ABC求出BC，从而求得。【例7】如图，正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直．（1）证明：Rt△ABM∽Rt△MCN；（2）设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN的面积最大，并求出最大面积；（3）当M点运动到什么位置时，Rt△ABM∽Rt△AMN？求此时x的值．考点5相似与梯形【例8】如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.33相似和四边形 【规律方法】注意分类讨论。归纳总结﹒思维升华1.三角形相似的条件（1）三角形相似的预备定理平行于三角形一边的直线和其它两边相交，所构成的三角形与原三角形相似．(2)三边对应成比例，两三角形相似.(3)两边对应成比例且夹角相等，两三角形相似.(4)两角对应相等，两三角形相似.2.如何寻找和发现相似三角形两个三角形相似，一般说来必须具备下列六种图形之一：相似型的基本图形回顾：（1）A型（2）8型（也叫X型）33相似和四边形 （3）K型（4）双垂直型：（也叫母子型）由Rt△DAC∽Rt△DBA∽Rt△ABC，得AB2＝BD·BC，AC2=CD·BC，AD2=BD·CD。熟记这三个等式有时会给解题带来很大的方便，尤其解几何综合题更明显，但须注意，在使用它们时，一定要证明这三个直角三角形相似．33相似和四边形 只要能在复杂图形中辨认出上述基本图形，并能根据问题需要添加适当的辅助线，构造出基本图形，从而使问题得以解决.3.相似三角形与相似多边形的性质①相似三角形的三边对应成比例，三角对应相等.②相似三角形的对应高之比，对应角平分线之比与对应中线之比都等于相似比.③相似三角形周长之比等于相似比，相似三角形面积之比等于相似比的平方.专题训练﹒对接中考1.如图，在矩形ABCD中，AB=9，BC=12，点E是BC中点，点F是边CD上的任意一点，当△AEF的周长最小时，则DF的长为（　　）A．4B．6C．8D．92.如图3，菱形中，，点、分别为边、上的点，且,连接、交于点，则下列结论：①≌；②；③∽；④；其中结论正确的个数是（*）．A．1个B．2个C．3个D．4个33相似和四边形 3.如图，直角梯形ABCD中，∠BCD＝90°，AD∥BC，BC＝CD，E为梯形内一点，且∠BEC＝90°，将△BEC绕C点旋转90°使BC与DC重合，得到△DCF，连EF交CD于M．已知BC＝5，CF＝3，则DM:MC的值为（　　）A.5:3B.3:5C.4:3D.3:4ADBCEFM4.如图，四边形ABCD、CEFG都是正方形，点G在线段CD上，连接BG、DE，DE和FG相交于点O．设AB=a，CG=b(a＞b)．下列结论：①△BCG≌△DCE；②BG⊥DE；③；④．其中结论正确的个数是（）A．1个B.2个C.3个D.4个二、填空题1.下图中，E为平行四边形ABCD的对角线AC上一点，AE∶EC=1∶3，BE的延长线交CD的延长线于G，交AD于F，则BF∶FG=_________.33相似和四边形 2.如图，在△ABC中，有矩形DEFG，G、F在BC上，D、E分别在AB、AC上，AH⊥BC交DE于M，DG∶DE＝1∶2，BC＝12cm，AH＝8cm，求矩形的长是，宽是。3.如图，在正方形中，边长为2的等边三角形的顶点、分别在和上．下列结论：①CE=CF；ABCDEF第3题图②∠AEB=75°；③BE＋DF=EF；④=．其中正确的序号是______________．（把你认为正确的都填上）4.如图，将边长为6的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为FH，点C落在点Q处，EQ与BC交于点G，则△EBG的周长是_____cm.三、解答题33相似和四边形 1．如图9，现有一张边长为的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合），将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．（1）求证：∠APB=∠BPH；（2）当点P在边AD上移动时，求证：△PDH的周长是定值；（3）当BE+CF的长取最小值时，求AP的长．图92.在平面直角坐标系中，O为原点，点B在x轴的正半轴上，D（0，8），将矩形OBCD折叠，使得顶点B落在CD边上的P点处。（1）如图①，已知折痕与边BC交于点A，若OD=2CP，求点P的坐标；33相似和四边形 （2）若图①中的点P恰好是CD边的中点，求∠AOB的度数；（3）如图②，在（1）的条件下，擦去折痕AO，线段AP，连接BP，动点M在线段OP上（点M不与P，O重合），动点N在线段OB的延长线上，且BN=PM，连接MN交PB于点F，作ME⊥BP于点E，试问当点M，N在移动过程中，线段EF的长度是否发生变化？若变化，说明理由；若不变，请求出线段EF的长度.第25题图①第25题图②33相似和四边形 作业一、选择题1.如图，平行四边形ABCD中，、、为对角线BD上三点，且B＝＝＝D，连结A并延长交BC于点E，连结E并延长交AD于F，则AD:FD等于（）A.19:2B.9:1C.8:1D.7:1第2题图2．如图，在正方形ABCD的外侧，作等边△ADE，BE、CE分别交AD于G、H，设△CDH、△GHE的面积分别为S1、S2，则()A．3S1=2S2B．2S1=3S2C．2S1=S2D．S1=2S23.如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，则下列结论中：错误的是()A．；B.；C.；D..33相似和四边形 二、填空题1.如图，某测量工作人员与标杆顶端F、电视塔顶端在同一直线上，已知此人眼睛距地面1.6米，标杆为3.2米，且BC=1米，CD=5米，电视塔的高ED为_______米。第2题图2.如图，正方形DEMF内接于△ABC，若=________3.如图，在边长为1的正方形ABCD的一边BC上，任取一点E，作EF⊥AE交CD于点F，如果BE＝x，CF＝y，那么用x的代数式表示y是_____________4．如图，等边△ABC的边长为3，P为BC上一点，且BP＝1，D为AC上一点，若∠APD＝60°，则CD的长为________三、解答题1.已知：如图，在矩形中，=4，=8，，分别是边，上的点．若，33相似和四边形 =2，求的长；2.如图，在直角△ABC内，以A为一个顶点作正方形ADEF，使得点E落在BC边上.(1)用尺规作图，作出D、E、F中的任意一点(保留作图痕迹，不写作法和证明。另外两点不需要用尺规作图确定，作草图即可)；(2)若AB=6，AC=2，求正方形ADEF的边长.3.已知：如图所示的一张矩形纸片ABCD（AD>AB），将纸片折叠一次，使点A与点C重合，再展开，折痕EF交AD边于点E，交BC边于点F，分别连结AF和CE。33相似和四边形 （1）求证：四边形AFCE是菱形；（2）若AE=10cm，△ABF的面积为24cm2，求△ABF的周长；（3）在线段AC上是否存在一点P，使得2AE2=AC·AP？若存在，请说明点P的位置，并予以证明；若不存在，请说明理由.ABCDEFO4.如图，正方形ABCD的边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直。（1）证明：Rt△ABM～Rt△MCN（2）设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN的面积最大，并求出最大面积；33相似和四边形 （1）当M点运动到什么位置时Rt△ABM～Rt△AMN,求此时x的值。33相似和四边形 参考答案：热点聚焦﹒考点突破【例1】在平行四边形ABCD中，AB=CD=6，AD=BC=9，∠BAD的平分线交BC于点E，可得△ADF是等腰三角形，AD=DF=9；△ADF是等腰三角形，AB=BE=6，所以CF=3；在△ABG中，BG⊥AE，AB=6，BG=，可得AG=2，又△ADF是等腰三角形，BG⊥AE，所以AE=2AG=4，所以△ABE的周长等于16，又由平行四边形ABCD可得△CEF∽△BEA，相似比为1：2，所以△CEF的周长为8．故选A.点评：此类问题难度较大，在中考中比较常见，一般在压轴题中出现，需特别注意【例2】证明：∵AD∥BC，∴△ADE∽△GBE，∴．∵DF∥AB，∴△DEF∽△BEA，∴，∴．∴AE2=EF·EG．ABCFGED【例3】解：设经x秒后，△PBQ与△BCD相似，由于∠PBQ=∠BCD=90°(1)当1=2时，有即33相似和四边形 (2)当1=3时，有即∴经过秒或2秒，△PBQ与△BCD相似.【例4】解：（1）由矩形，得:，．在中，∵，，∴，．又∵，∴ ．于是，由，得．（2）联结．在中，．∴，即得:．∵，∴．又∵，点为线段的中点，∴，．∴．在中，．33相似和四边形 ∴，即得，．由勾股定理，得．于是，由，，得:．（3）．证明如下：过点作，垂足为点．∵，，∴．在中，由，得 ，即得．∵，∴ ,，即得 ，．∴．于是，由，得:．【例5】25．（本题满分14分）解：（1）当顶点与重合时，折痕垂直平分，∴…………………………………………1分在矩形中，，33相似和四边形 ∴…………………………………………………………………2分∴≌∴…………………………………………………………………3分∴四边形是菱形．………………………………………………………4分（2）证明：∵∴，∵，∴……………………………………………………………5分∵∴∽…………………………………………………………………7分∴∴…………………………………………………………………9分（3）四边形是菱形∴……………………………10分在中，…………………………………………11分∴∴①……………………………………12分∵的面积为∴∴②……………………………………………………13分由①、②得：AEDCFBPO∵∴……………………33相似和四边形 【例6】如图，正方形DEMF内接于△ABC，若，，求解：∵正方形的面积为4，∴DE＝MF＝2。过A点作AQ⊥BC于Q，交DE于P∵，∴AP＝1∵DE∥BC，∴△ADE∽△ABC，∴，即∴BC＝6，故＝9【例7】解：（1）证明：∵四边形ABCD为正方形，∴∠B=∠C=90°，∵∠AMB+∠BAM=90°，又∴AM⊥MN，∴∠AMN=90°，∴∠AMB+∠NMC=90°，∴∠BAM=∠NMC，∴Rt△ABM∽Rt△MCN；33相似和四边形 （2）解：∵正方形ABCD边长为4，BM=1，∴CM=4-1=3，∵Rt△ABM∽Rt△MCN，∴，即，∴CN=，∴S梯形ABCN=（AB+CN）BC=×（4+）×4=；∴正方形ABCD边长为4，BM=x，∴CM=4﹣x，∴Rt△ABM∽Rt△MCN，∴，即，∴CN=，∴y=S梯形ABCN=（AB+CN）BC=×（4+）×4=﹣x2+2x+8=﹣（x﹣2）2+10，∵当x=2时，四边形ABCN的面积最大，最大面积为10；（3）解：∵∠B=∠AMN=90°，∴要使Rt△ABM∽Rt△AMN，必须有，即，∵Rt△ABM∽Rt△MCN，∴，∴BM=MC，∴当点M运动到BC的中点时，Rt△ABM∽Rt△AMN，此时BM=2．考点5相似与梯形【例8】解：存在．∵AD∥BC，∠A=90°，∴∠B=90°，33相似和四边形 当△PAD∽△PBC时，=∵AB=AP+PB=7，AD=2，BC=3，∴AP=；当△ADP∽△BPC时，=∵AB=AP+PB=7，AD=2，BC=3，∴PA=1或PA=6；由①②可知，P点距离A点有三个位置：PA=；PA=1或PA=6．专题训练﹒对接中考一．选择题：1.B；2.D；3.C4.B2.分析：∵四边形ABCD是菱形，∴AB=BC，∵AB=AC，∴AB=BC=AC，即△ABC是等边三角形，同理：△ADC是等边三角形∴∠B=∠EAC=60°，在△ABF和△CAE中，BF=AE∠B=∠EAC33相似和四边形 BC＝AC∴△ABF≌△CAE（SAS）；故①正确；∴∠BAF=∠ACE，∵∠AEH=∠B+∠BCE，∴∠AHC=∠BAF+∠AEH=∠BAF+∠B+∠BCE=∠B+∠ACE+∠BCE=∠B+∠ACB=60°+60°=120°；故②正确；③由①得∠EAH=∠ACE,∠AEC=AFB∴△AEH∽△CEA④由③得△AEH∽△CEA∴△AEH∽△ABF∴∵AB=AD∴∴AE.AD=AF.AH二、填空题1.1:22.cm，cm3.①②④4.12三、解答题1．（2015年越秀区一模）25．（本小题满分14分）（1）解：如图1，∵PE=BE，33相似和四边形 ∴∠EBP=∠EPB．………………1分又∵∠EPH=∠EBC=90°，∴∠EPH﹣∠EPB=∠EBC﹣∠EBP．即∠PBC=∠BPH．………………2分又∵AD∥BC，∴∠APB=∠PBC．∴∠APB=∠BPH．………………3分（2）证明：如图2，过B作BQ⊥PH，垂足为Q．由（1）知∠APB=∠BPH，又∵∠A=∠BQP=90°，BP=BP，∴△ABP≌△QBP．………………4分∴AP=QP，AB=BQ．又∵AB=BC，∴BC=BQ．………………5分又∵∠C=∠BQH=90°，BH=BH，∴△BCH≌△BQH．∴CH=QH．………………6分∴△PHD的周长为：PD+DH+PH=AP+PD+DH+HC=AD+CD=8．∴的周长是定值………………7分（3）解：如图3，过F作FM⊥AB，垂足为M，则FM=BC=AB．又∵EF为折痕，∴EF⊥BP．∴∠EFM+∠MEF=∠ABP+∠BEF=90°，∴∠EFM=∠ABP．又∵∠A=∠EMF=90°，∴△EFM≌△BPA．………………8分∴EM=AP．………………9分设AP=x33相似和四边形 在Rt△APE中，（4﹣BE）2+x2=BE2．解得，．………………11分∴．………………12分∴．………………13分当时，取最小值∴………………14分【2】25．（本小题满分14分）解：（1）∵D（0，8），∴OD=BC=8∵OD=2CP，∴CP=4设DP=x∵矩形OBCD折叠，使得顶点B落在CD边上的P点处∴△OAB≌△OAP∴OB=OP=DC=x+4………1分在Rt△ODP中，解得：x=6∴P(6，8).………2分(2)∵点P恰好是CD边的中点，∴设DP=PC=y，则DC=OB=OP=2y，………3分在Rt△ODP中，即33相似和四边形 解得：，………4分∵矩形OBCD折叠，使得顶点B落在CD边上的P点处∴△OAB≌△OAP∵∠OPA=∠B=90°，∴∠DPO+∠CPA=90°∵∠DPO+∠POD=90°,∴∠CPA=∠POD∵∠D=∠C=90°,∴△ODP∽△PCA，………5分∴，即∴，………6分∵，∴∴∠AOB=30°………7分（3）猜想：线段EF的长度不发生变化………8分过点M作MQ∥OB交PB于点Q，∵OP=OB，MQ∥ON∴∠OPB=∠OBP=∠MQP∴MP=MQ………9分∵MP=MQ，ME⊥PQ，∴………10分∵MQ∥AN，∴∠QMF=∠BNF∵BN=PM，∴BN=QM………11分在△MFQ和△NFB中，33相似和四边形 ∴△MFQ≌△NFB∴………12分∴………13分由（1）中的结论可得：PC=4，BC=8，∠C=90°，∴∴∴在（1）的条件下，当点M、N在移动过程中，线段EF的长度不变，EF的长度为…14分作业:一、选择题1.B2.A3.C二、填空题1.11.22.93.y=4.三、解答题1.解：∵矩形ABCD，∴∠B=∠C=90°，∴∠BAP+∠BPA=90°∵AP⊥PQ，∴∠APQ=90°，∴∠BPA+∠CPQ=90°，∴∠BAP=∠CPQ∴△ABP～△PCQ，∴CQ=32.(1)提示：作∠A的平分线交BC于点E。33相似和四边形 （2）∵四边形ADEF为正方形，∴设AF=EF=x，∴△CFE～△CAB∴3.分析：（1）由四边形ABCD是矩形与折叠的性质，易证得△AOE≌△COF，即可得AE=CF，则可证得四边形AFCE是平行四边形，又由AC⊥EF，则可证得四边形AFCE是菱形；由已知可得：S△ABF=AB•BF=24cm2，则可得AB2+BF2=（AB+BF）2-2AB•BF=（AB+BF）2-2×48=AF2=100（cm2），则可求得AB+BF的值，继而求得△ABF的周长．过E作EP⊥AD交AC于P，则P就是所求的点，首先证明四边形AFCE是菱形，然后根据题干条件证明△AOE∽△AEP，列出关系式．试题解析：（1）∵四边形ABCD是矩形，∴AD∥BC，∴∠EAO=∠FCO，由折叠的性质可得：OA=OC，AC⊥EF，在△AOE和△COF中，∵ ，∴△AOE≌△COF（ASA），∴AE=CF，∴四边形AFCE是平行四边形，∵AC⊥EF，∴四边形AFCE是菱形；（2）∵四边形AFCE是菱形，∴AF=AE=10cm，∵四边形ABCD是矩形，∴∠B=90°，33相似和四边形 ∴S△ABF=AB•BF=24cm2，∴AB•BF=48（cm2），∴AB2+BF2=（AB+BF）2-2AB•BF=（AB+BF）2-2×48=AF2=100（cm2），∴AB+BF=14（cm）∴△ABF的周长为：AB+BF+AF=14+10=24（cm）．（3）证明：过E作EP⊥AD交AC于P，则P就是所求的点．当顶点A与C重合时，折痕EF垂直平分AC，∴OA=OC，∠AOE=∠COF=90°，∵在平行四边形ABCD中，AD∥BC，∴∠EAO=∠FCO，∴△AOE≌△COF，∴OE=OF∴四边形AFCE是菱形．∴∠AOE=90°，又∠EAO=∠EAP，由作法得∠AEP=90°，∴△AOE∽△AEP，∴，则AE2=A0•AP，∵四边形AFCE是菱形，∴AO＝AC，∴AE2=AC•AP，∴2AE2=AC•AP．4.解：（1）证明：∵四边形ABCD为正方形，∴∠B=∠C=90°，∵∠AMB+∠BAM=90°，又∴AM⊥MN，∴∠AMN=90°，∴∠AMB+∠NMC=90°，∴∠BAM=∠NMC，∴Rt△ABM∽Rt△MCN；33相似和四边形 （2）AM=PM．证明：∵四边形ABCD为正方形，∴AB=BC，∠B=∠BCD=90°，∴AH=MC，∵BH=BM，∴∠BMH=∠BHM=45°，∠AHM=135°，∵AM⊥MN，∴∠2+∠3+∠BMH=90°，∵∠2+∠3=45°，∴∠1+∠2=∠BHM=45°，∴∠1=∠3，∵CP是正方形外角平分线，∴∠PCN=45°，∴∠PCM=90°+45°=135°，∴∠AHM=∠MCP，在△AHM和△MCP中，∵，∴△AHM∽△MCP（ASA），∴AM=PM；（3）解：∵正方形ABCD边长为4，BM=1，∴CM=4-1=3，∵Rt△ABM∽Rt△MCN，∴，即，∴CN=，∴S梯形ABCN=（AB+CN）BC=×（4+）×4=；∴正方形ABCD边长为4，BM=x，∴CM=4﹣x，∴Rt△ABM∽Rt△MCN，∴，即，∴CN=，∴y=S梯形ABCN=（AB+CN）BC=×（4+）×4=﹣x2+2x+8=﹣（x﹣2）2+10，∵当x=2时，四边形ABCN的面积最大，最大面积为10；（4）解：∵∠B=∠AMN=90°，∴要使Rt△ABM∽Rt△AMN，必须有，即，∵Rt△ABM∽Rt△MCN，∴，∴BM=MC，33相似和四边形 ∴当点M运动到BC的中点时，Rt△ABM∽Rt△AMN，此时BM=2．33相似和四边形