北师大八年级数学（下册）期末测试卷（附参考答案）

北师大八年级数学（下册）期末测试卷（附参考答案）

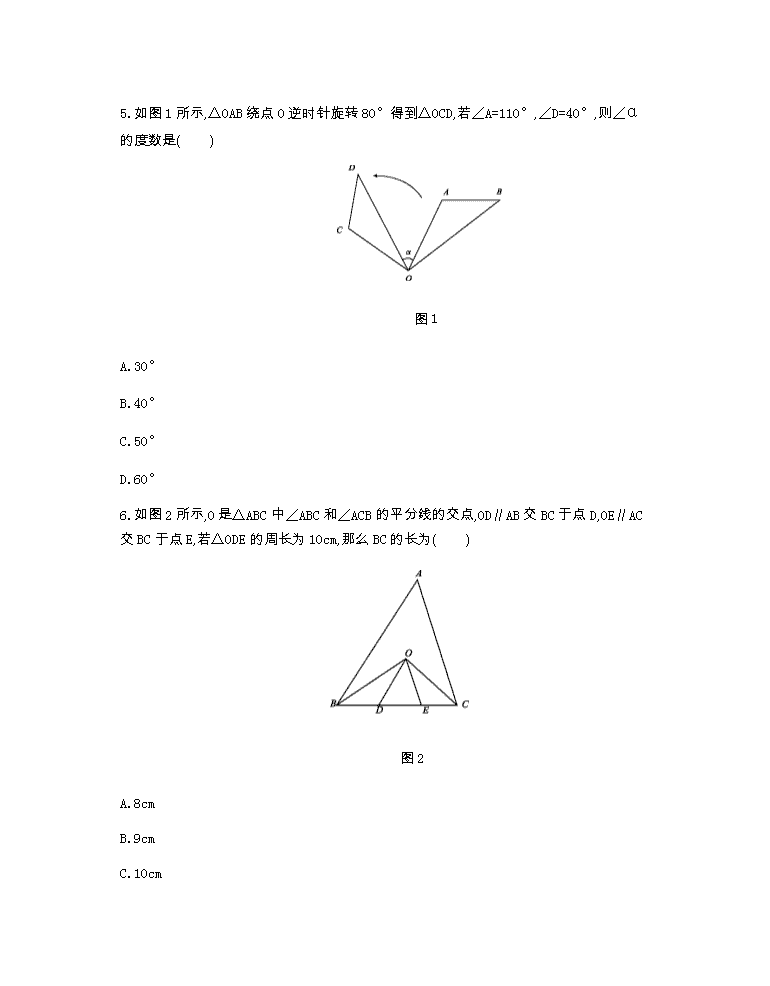
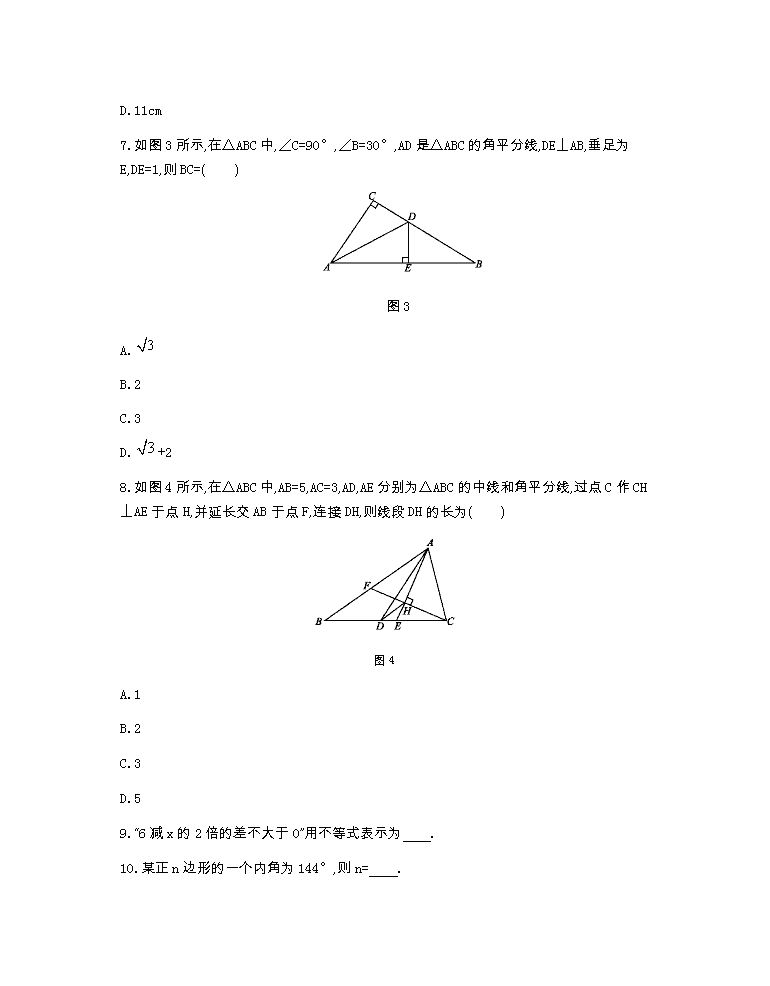
期末测试卷 ‎（考试时间：90分钟 满分：100分）‎ ‎1.要使分式有意义,则x的取值范围是(　　)‎ A.x>2 B.x<2 C.x≠-2 D.x≠2‎ ‎2.下面给出四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判别四边形ABCD是平行四边形的是(　　)‎ A.1∶2∶3∶4‎ B.2∶3∶2∶3‎ C.2∶3∶3∶2‎ D.1∶2∶2∶3‎ ‎3.不等式x-3≤3x+1的解集在数轴上表示如下,其中正确的是(　　)‎ A.‎ B.‎ C.‎ D.‎ ‎4.分解因式a-ab2的结果是(　　)‎ A.a(1+b)(1-b) B.a(1+b)2 C.a(1-b)2 D.a(1-b2)‎ ‎5.如图1所示,△OAB绕点O逆时针旋转80°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是(　　)‎ ‎ ‎ 图1‎ A.30°‎ B.40°‎ C.50°‎ D.60°‎ ‎6.如图2所示,O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于点D,OE∥AC交BC于点E,若△ODE的周长为10cm,那么BC的长为(　　)‎ ‎ ‎ 图2‎ A.8cm B.9cm C.10cm D.11cm ‎7.如图3所示,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=(　　)‎ ‎ ‎ 图3‎ A.‎ B.2‎ C.3‎ D.+2‎ ‎8.如图4所示,在△ABC中,AB=5,AC=3,AD,AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连接DH,则线段DH的长为(　　)‎ 图4‎ A.1‎ B.2‎ C.3‎ D.5‎ ‎9.“6减x的2倍的差不大于0”用不等式表示为　　. ‎ ‎10.某正n边形的一个内角为144°,则n=　　. ‎ ‎11.制作某种机器零件,小明做220个零件与小芳做180个零件所用的时间相同,已知小明每小时比小芳多做20个零件.设小芳每小时做x个零件,则可列方程为 　. ‎ ‎12.若关于x的方程产生增根,则m的值是　　. ‎ ‎13.如图5所示,四边形AEFD和四边形EBCF都是平行四边形,则四边形ABCD是　　. ‎ 图5‎ ‎14.如图6所示,在△AOB中,AO=AB,在平面直角坐标系中,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A’O’B’,使得点A’在y轴上,点O’,B’在x轴上,则点B’的坐标是　　. ‎ ‎ ‎ 图6‎ ‎15.分式与分式方程:‎ ‎(1)先化简,再求值:·,其中a=-.‎ ‎(2)=2;‎ ‎16.解不等式组并把解集表示在数轴上.‎ ‎17.如图7所示,已知单位长度为1的方格中有一个△ABC.‎ ‎(1)请画出△ABC向上平移3格再向右平移3格所得△A’B’C’;‎ ‎(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,点B’的坐标:B(　　,　　),B’(　　,　　). ‎ 图7‎ ‎18.如图8所示,在△ABC中,AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△ACD’,连接D’E,已知DE=D’E.‎ ‎(1)求证:△ADE≌△AD’E;‎ ‎(2)若∠BAC=120°,求∠DAE的度数.‎ 图8‎ ‎19.如图9所示,在四边形ABCD中,AD∥BC,∠ABD=30°,DC⊥BC于点C,点A是BD垂直平分线上的点.若BD=2,求CD的长.‎ 图9‎ ‎20.如图10所示,线段AC,BD相交于点O,AB∥CD,AB=CD.线段AC上的两点E,F关于点O中心对称.求证:BF=DE.‎ 图10‎ ‎21.某厂制作甲、乙两种环保包装盒,已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个,且制作一个甲盒比制作一个乙盒需要多用20%的材料.求制作每个甲盒、乙盒各用多少材料?‎ ‎22.阅读下列分解因式的过程:‎ x4+4=x4+4x2+4-4x2　　　　　　　①‎ ‎=(x2+2)2-(2x)2‎ ‎=[(x2+2)+2x][(x2+2)-2x]‎ ‎=(x2+2x+2)(x2-2x+2).‎ ‎(1)①中加上4x2的目的是　　,减去4x2的目的是　　. ‎ 在分解因式时,可通过加项、减项、拆项等方法配出完全平方式,然后在此基础上进行分解,这种分解方法叫做配方法分解因式.‎ ‎(2)试用(1)中的方法分解因式:x4-3x2+1.‎ ‎23.某工厂现有甲种原料280kg,乙种原料190kg,计划用这两种原料生产A,B两种产品50件,已知生产一件A产品需甲种原料7kg、乙种原料3kg,可获利400元;生产一件B产品需甲种原料3kg,乙种原料5kg,可获利350元.‎ ‎(1)请问工厂有哪几种生产方案?‎ ‎(2)选择哪种方案可获利最大,最大利润是多少?‎ 参考答案 ‎1.D ‎2.B ‎3.B ‎4.A ‎5.C ‎6.C ‎7.C ‎8.A ‎9.6-2x≤0‎ ‎10.10‎ ‎11.‎ ‎12.2‎ ‎13.平行四边形 ‎14.(2,0)‎ ‎15.(1)解:原式=··,‎ 当a=-时,原式=-1.‎ ‎(2)解:方程两边同乘(2x-1),得10-5=2(2x-1),‎ 解得x=.‎ 经检验,x=是原方程的解.‎ ‎16.解:解不等式①,得x≤3.‎ 解不等式②,得x>-2.‎ 所以不等式组的解集是-2

查看更多