七年级下数学课件《证明》 (3)_苏科版

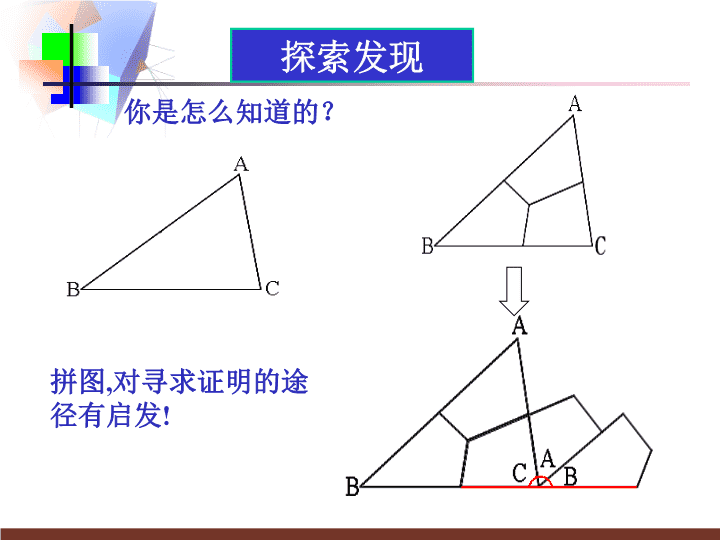
七年级下数学课件《证明》 (3)_苏科版

初中数学七年级下册（苏科版）12.2证明（3） 你知道吗？180°三角形3个内角的和是.°探索发现 你是怎么知道的？拼图,对寻求证明的途径有启发!探索发现 如何证明三角形内角和等于180°？试一试！探索发现 ABC12DE已知:△ABC求证:∠A+∠B+∠C=180°证明:如图,作BC的延长线CD,过点C作CE∥AB.∠1=∠A(两直线平行,内错角相等)∠2=∠B(两直线平行,同位角相等)∵∠1+∠2+∠ACB=180°（平角的定义）∴∠A+∠B+∠ACB=180°(等量代换).探索发现探索发现 ABCED你还有什么不同的方法?ABCPHQEBCDA探索发现 关于辅助线1.辅助线是为了证明需要在原图上添画的线.（辅助线通常画成虚线）2.它的作用是把分散的条件集中，把隐含的条件显现出来，起到牵线搭桥的作用.3.添加辅助线，可构造新图形，形成新关系，找到联系已知与未知的桥梁，把问题转化，但辅助线的添法没有一定的规律，要根据需要而定,平时做题时要注意总结. 三角形内角和定理：三角形三个内角的和等于180°。归纳总结 如图，∠α是△ABC的一个外角，∠α与△ABC的内角有怎样的大小关系？由三角形内角和定理，可以知道：∠α=∠A+∠B三角形内角和定理的推论：1.三角形的一个外角等于和它不相邻的两个内角的和；2.三角形的一个外角大于任何一个和它不相邻的内角.进而，∠α>∠A，∠α>∠B.αCBAγβ探索发现 1.证明：直角三角形两个锐角互余。求证：∠A＋∠B＝90°已知：如图，△ABC中，∠C=90°证明:∵∠A＋∠B＋∠C=180°(三角形的内角和定理)∴∠A＋∠B=180°-∠C又∵∠C=90°∴∠A＋∠B=180°-90°=90°课堂练习 2.如图，∠α、∠β、∠γ是△ABC的3个外角；猜想△ABC的3个外角的和是多少？证明你的猜想。解：∠α+∠β+∠γ=360°∵∠1+∠α=180°∠2+∠β=180°∠3+∠γ=180(平角的定义)∴∠1+∠α+∠2+∠β+∠3+∠γ=540°∴∠α+∠β+∠γ=540°-(∠1+∠2+∠3)=540°-180°=360°γβCBAα⌒1⌒23⌒课堂练习 3、四边形的内角和等于多少度？证明你的结论.已知：四边形ABCD求证：∠A+∠B+∠C+∠D=360°.证明:连接AC∵∠1+∠2+∠D=180°∠3+∠4+∠B=180°(三角形的内角和定理)ABCD⌒⌒⌒2⌒134∴∠1+∠2+∠D+∠3+∠4+∠B=360°又∵∠DAB=∠1+∠3∠DCB=∠2+∠4∴∠DAB+∠B+∠DCB+∠D=360°(等量代换)即四边形的内角和等于360°课堂练习 通过这节课的学习,你有哪些收获？1.我们通过添加辅助线,把三角形的3个内角拼成1个平角;把三角形的3个内角拼成两平行线的同旁内角,证明了三角形内角和定理及推论.2.继续感受数学的严谨、结论的确定，初步养成言之有理、落笔有据的推理习惯，发展初步的演绎推理能力.课堂小结 已知:如图，D是△ABC内的任意一点.求证:∠BDC=∠1+∠A+∠2ABDCQ⌒⌒12课后练习