高考数学二轮复习教案：基础保分强化训练(四)

高考数学二轮复习教案：基础保分强化训练(四)

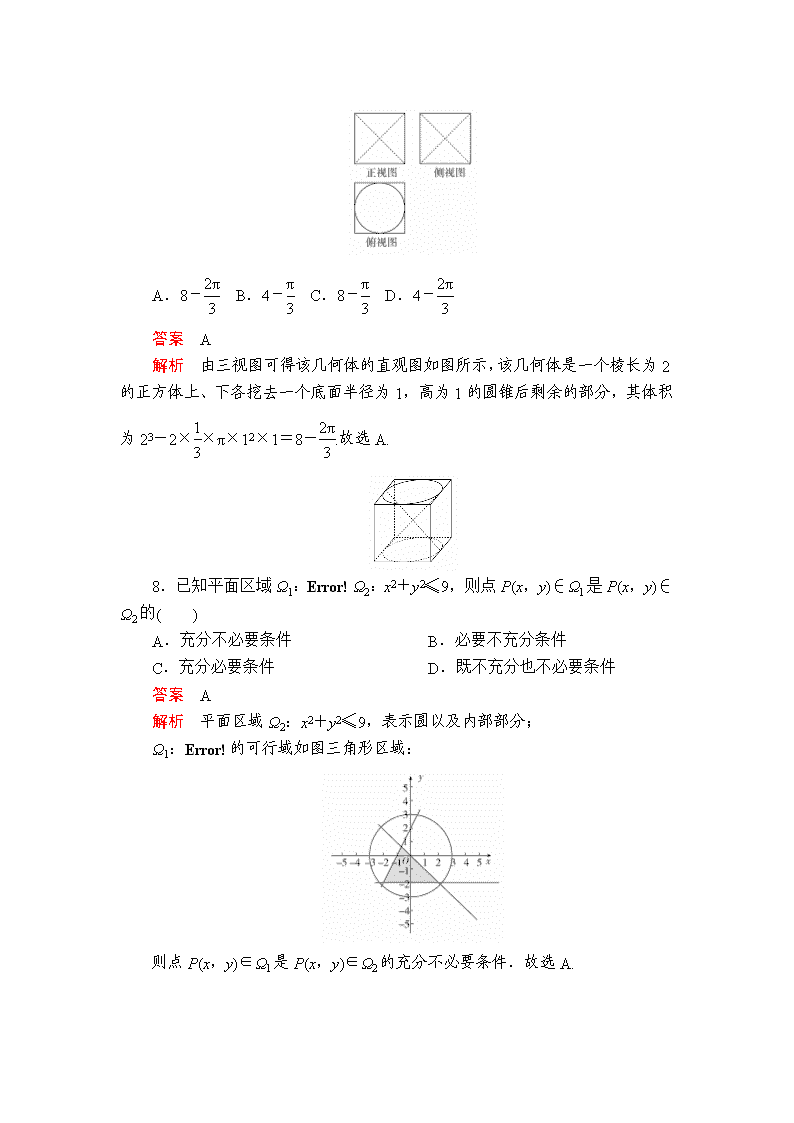
基础保分强化训练(四)‎ ‎1．集合A＝{x|x2－a≤0}，B＝{x|x<2}，若A⊆B，则实数a的取值范围是(　　)‎ A．(－∞，4] B．(－∞，4)‎ C．[0,4] D．(0,4)‎ 答案　B 解析　当a<0时，集合A＝∅，满足题意；当a≥0时，A＝[－， ]，若A⊆B，则<2，所以0≤a＜4，所以a∈(－∞，4)，故选B.‎ ‎2．已知复数z满足z＋|z|＝3＋i，则z＝(　　)‎ A．1－i B．1＋i C.－i D.＋i 答案　D 解析　设z＝a＋bi，其中a，b∈R，由z＋|z|＝3＋i，得a＋bi＋＝3＋i，由复数相等可得 解得故z＝＋i，故选D.‎ ‎3．已知直线l：y＝kx＋1与圆O：x2＋y2＝2相交于A，B两点，则“k＝1”是“∠AOB＝120°”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 答案　A 解析　由题意得圆心(0,0)到直线l：y＝kx＋1的距离为d＝，若∠AOB＝120°，则有＝×，得k2＝1即k＝±1，若k＝1时，则∠AOB＝120°，但∠AOB＝120°时，k＝－1或k＝1，故选A.‎ ‎4．将数字1,2,3填入编号为4,5,6的三个方格中，每个方格填上一个数字，则恰有一个方格的编号与所填的数字之差为3的概率是(　　)‎ A. B. C. D. 答案　C 解析　将数字1,2,3填入编号为4,5,6的三个方格中，其基本事件为(1,2,3)，(1,3,2)，(2,1,3)，(2,3,1)，(3,2,1)，(3,1,2)，共有6个，其中恰有一个方格的编号与所填的数字之差为3的事件有(1,3,2)，(2,1,3)，(3,2,1)，所以恰有一个方格的编号与所填的数字之差为3的概率P＝＝.故选C.‎ ‎5．在△ABC中，M是BC的中点，AM＝1，点P在AM上且满足＝2‎ ，则·(＋)等于(　　)‎ A．－ B．－ C. D. 答案　A 解析　如图，∵＝2，∴＝＋，∴·(＋)＝－2，∵AM＝1且＝2，∴||＝，∴·(＋)＝－，故选A.‎ ‎6．下列函数中，既是奇函数又在(－∞，＋∞)上单调递增的是(　　)‎ A．y＝sinx B．y＝|x|‎ C．y＝－x3 D．y＝ln (＋x)‎ 答案　D 解析　sinx不是单调递增函数，可知A错误；|－x|＝|x|，则函数y＝|x|为偶函数，可知B错误；y＝－x3在(－∞，＋∞)上单调递减，可知C错误；ln (－x)＝ln ＝－ln (＋x)，则y＝ln (＋x)为奇函数；当x≥0时，＋x单调递增，由复合函数单调性可知y＝ln (＋x) 在[0，＋∞)上单调递增，根据奇函数对称性，可知在(－∞，＋∞)上单调递增，则D正确．故选D.‎ ‎7．一个几何体的三视图如图所示，图中的三个正方形的边长均为2，则该几何体的体积为(　　)‎ A．8－ B．4－ C．8－ D．4－ 答案　A 解析　‎ 由三视图可得该几何体的直观图如图所示，该几何体是一个棱长为2的正方体上、下各挖去一个底面半径为1，高为1的圆锥后剩余的部分，其体积为23－2××π×12×1＝8－.故选A.‎ ‎8．已知平面区域Ω1：Ω2：x2＋y2≤9，则点P(x，y)∈Ω1是P(x，y)∈Ω2的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 答案　A 解析　平面区域Ω2：x2＋y2≤9，表示圆以及内部部分；‎ Ω1：的可行域如图三角形区域：‎ 则点P(x，y)∈Ω1是P(x，y)∈Ω2的充分不必要条件．故选A.‎ ‎9．若ω>0，函数y＝cos的图象向右平移个单位长度后与函数y＝sinωx的图象重合，则ω的最小值为(　　)‎ A. B. C. D. 答案　B 解析　函数y＝cos的图象向右平移个单位长度后，所得函数图象对应的解析式为y＝cos＝cos，其图象与函数y＝sinωx＝cos，k∈Z的图象重合，∴－＋2kπ＝－＋，k∈Z，∴ω＝－6k＋，k∈Z ‎，又ω>0，∴ω的最小值为，故选B.‎ ‎10．设a＝log43，b＝log52，c＝log85，则(　　)‎ A．alog85，即a>c，∵2<，5>，‎ ‎∴c＝log85>log8＝，b＝log52log52，即c>b，∴log43>log85>log52，‎ 即a>c>b.故选B.‎ ‎11．已知双曲线C：－＝1(a>0，b>0)的左、右焦点分别为F1，F2，过原点的直线与双曲线C交于A，B两点，若∠AF2B＝60°，△ABF2的面积为a2，则双曲线的渐近线方程为(　　)‎ A．y＝±x B．y＝±2x C．y＝±x D．y＝±x 答案　D 解析　根据题意，连接AF1，BF1，AF2，BF2得四边形AF2BF1为平行四边形，几何关系如图所示，设|AF2|＝x，则|BF1|＝x，|BF2|＝x＋2a，△ABF2的面积为a2，∠AF2B＝60°，则由三角形面积公式可得a2＝x·(x＋2a)·，化简得x2＋2ax－4a2＝0，解得x＝(－1)a，x＝(－－1)a(舍去)．所以|BF2|＝(＋1)a.在△BF1F2中，|F1F2|＝2c，由余弦定理可得|F1F2|2＝|BF1|2＋|BF2|2－2|BF1|·|BF2|·cos120°，即(2c)2＝(－1)2a2＋(＋1)2a2－2(－1)a·(＋1)acos120°，化简可得c2＝4a2，由双曲线中c2＝a2＋b2，可得b2＝3a2，即＝±，所以渐近线方程为y＝±x，所以选D.‎ ‎12．已知函数f(x)＝则f＝________.‎ 答案　 解析　∵f＝ln ＝－1，∴f＝f(－1)＝e－1＝.‎ ‎13．如图，航空测量组的飞机航线和山顶在同一铅直平面内，已知飞机的飞行高度为10000 m，速度为50 m/s.某一时刻飞机看山顶的俯角为15°，经过420 s后看山顶的俯角为45°，则山顶的海拔高度为________ m．(取＝1.4，＝1.7)‎ 答案　2650‎ 解析　如图，作CD垂直于AB的延长线于点D，由题意知∠A＝15°，∠DBC＝45°，∴∠ACB＝30°，AB＝50×420＝21000.又在△ABC中，＝，∴BC＝×sin15°＝10500(－)．∵CD⊥AD，∴CD＝BC·sin∠DBC＝10500×(－)×＝10500×(－1)＝7350.‎ 故山顶的海拔高度h＝10000－7350＝2650(m)．‎ ‎14．将数列{an}中的所有项按每一行比上一行多1项的规则排成如下数阵：‎ 记数阵中的第1列数a1，a2，a4，…构成的数列为{bn}，Sn为数列{bn}的前n 项和．若Sn＝2bn－1，则a56＝________.‎ 答案　1024‎ 解析　当n≥2时，∵Sn＝2bn－1，∴Sn－1＝2bn－1－1，∴bn＝2bn－2bn－1，∴bn＝2bn－1(n≥2且n∈N*)，‎ ‎∵b1＝2b1－1，∴b1＝1，∴数列{bn}是首项为1，公比为2的等比数列，∴bn＝2n－1.设a1，a2，a4，a7，a11，…的下标1,2,4,7,11，…构成数列{cn}，则c2－c1＝1，c3－c2＝2，c4－c3＝3，c5－c4＝4，…，cn－cn－1＝n－1，累加得，cn－c1＝1＋2＋3＋4＋…＋(n－1)，∴cn＝＋1，由cn＝＋1＝56，得n＝11，∴a56＝b11＝210＝1024.‎