高考数学二轮复习教案：高难拉分攻坚特训(一)

申明敬告： 本站不保证该用户上传的文档完整性，不预览、不比对内容而直接下载产生的反悔问题本站不予受理。

文档介绍

高考数学二轮复习教案：高难拉分攻坚特训(一)

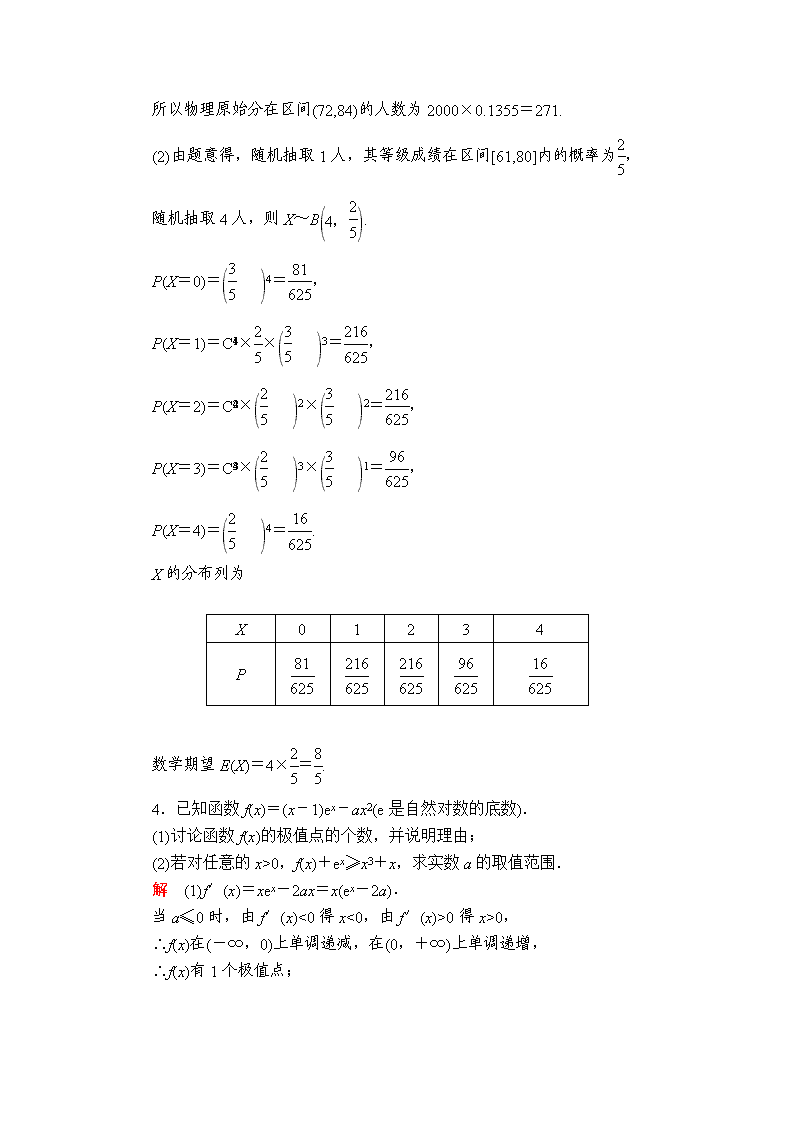
高难拉分攻坚特训(一)‎ ‎1．已知椭圆M：＋y2＝1，圆C：x2＋y2＝6－a2在第一象限有公共点P，设圆C在点P处的切线斜率为k1，椭圆M在点P处的切线斜率为k2，则的取值范围为(　　)‎ A．(1,6) B．(1,5) C．(3,6) D．(3,5)‎ 答案　D 解析　由于椭圆M：＋y2＝1，圆C：x2＋y2＝6－a2在第一象限有公共点P，所以解得30，f(x)＋ex≥x3＋x，求实数a的取值范围．‎ 解　(1)f′(x)＝xex－2ax＝x(ex－2a)．‎ 当a≤0时，由f′(x)<0得x<0，由f′(x)>0得x>0，‎ ‎∴f(x)在(－∞，0)上单调递减，在(0，＋∞)上单调递增，‎ ‎∴f(x)有1个极值点；‎ 当00得x0，由f′(x)<0得ln (2a)时，由f′(x)>0得x<0或x>ln (2a)，‎ 由f′(x)<0得00且a≠时，f(x)有2个极值点；‎ 当a＝时，f(x)没有极值点．‎ ‎(2)由f(x)＋ex≥x3＋x得xex－x3－ax2－x≥0.‎ 当x>0时，ex－x2－ax－1≥0，‎ 即a≤对任意的x>0恒成立．‎ 设g(x)＝，则g′(x)＝.‎ 设h(x)＝ex－x－1，则h′(x)＝ex－1.‎ ‎∵x>0，∴h′(x)>0，∴h(x)在(0，＋∞)上单调递增，‎ ‎∴h(x)>h(0)＝0，即ex>x＋1，‎ ‎∴g(x)在(0,1)上单调递减，在(1，＋∞)上单调递增，‎ ‎∴g(x)≥g(1)＝e－2，∴a≤e－2，‎ ‎∴实数a的取值范围是(－∞，e－2]．‎
查看更多

相关文章

您可能关注的文档