- 2021-07-01 发布 |
- 37.5 KB |
- 5页

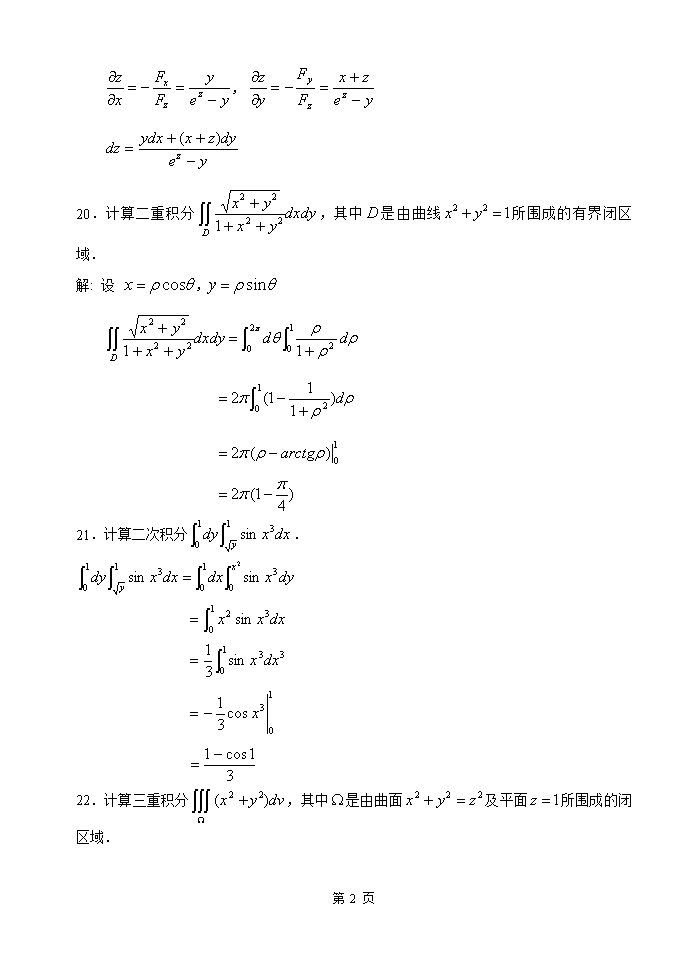

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高等数学模拟卷1解答
高等数学模拟卷1解答 一.单项选择题(本大题共10小题,每小题2分,共20分),在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内.错选、多选或未选均无分. 1、A;2、D;3、D;4、A;5、D;6、B;7、C;8、C;9、D;10、B;。 二.填空题(本大题共6小题,每小题3分,共18分),请在每小题的空格中填上正确答案,错填、不填均无分. 11. 12. 13. 14. 15. 16. 三.计算题(本大题共8小题,每小题6分,共48分). 17.求点在平面上的投影. 解: 过M垂直于平面的直线为 参数方程为,代入平面,得到 投影为 18.设,,可微,求,. 解: 19.设是由方程所确定的隐函数,求. 解 设 , , 第 5 页 , 20.计算二重积分,其中是由曲线所围成的有界闭区域. 解: 设 , 21.计算二次积分. 22.计算三重积分,其中是由曲面及平面所围成的闭区域. 第 5 页 解: 23.计算曲线积分,其中是由点到点的上半圆周. 解: 添加直线段,在由与构成的闭合曲线上运用格林公式:,, , 24.计算,其中是上半球面的上侧. 解: 添加辅助曲面:,,取下侧. 设, , 在由和所围成的空间闭区域上应用高斯公式得 第 5 页 又 , 因为取下侧. 所以 四.应用与证明题(本大题共2小题,每小题7分,共14分). 25.求由曲面及所围成的立体的体积. 解: ,可得(舍去)或者 两个曲面的交线在面上的投影区域为 26.已知平面区域,为的正向边界, 试证:. 证: 由格林公式: 第 5 页 又区域关于对称, 故 因此 第 5 页查看更多