浙江省2021届高考数学一轮复习第八章立体几何与空间向量第4节直线平面平行的判定及其性质课件

浙江省2021届高考数学一轮复习第八章立体几何与空间向量第4节直线平面平行的判定及其性质课件

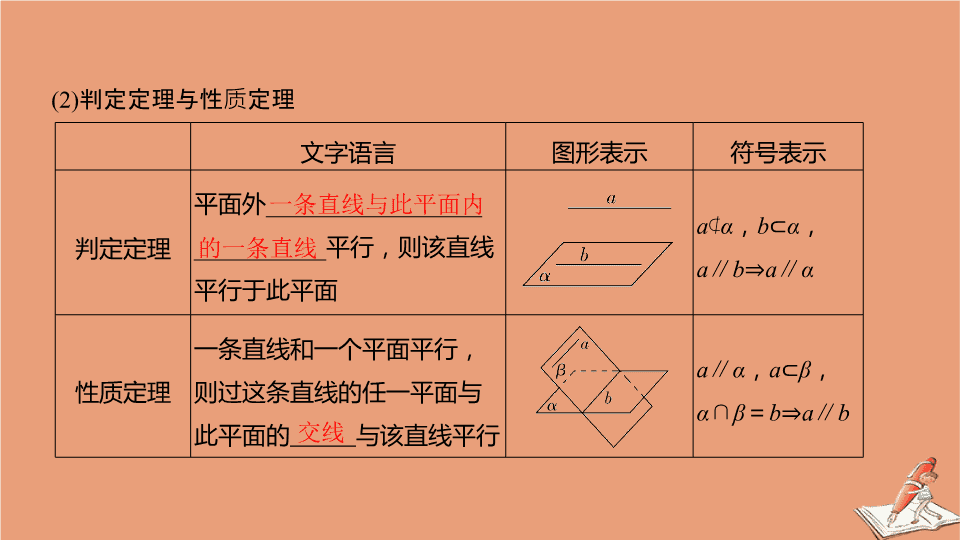
第 4 节　直线、平面平行的判定及其性质 考试要求　 1. 以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理； 2. 能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题 . 知 识 梳 理 1 . 直线与平面平行 (1) 直线与平面平行的定义 直线 l 与平面 α 没有公共点，则称直线 l 与平面 α 平行 . (2) 判定定理与性质定理   文字语言 图形表示 符号表示 判定定理 平面 外 __________________ ___________ 平行 ，则该直线平行于此平面 a ⊄ α ， b ⊂ α ， a ∥ b ⇒ a ∥ α 性质定理 一条直线和一个平面平行，则过这条直线的任一平面与此平面 的 与 该直线平行 a ∥ α ， a ⊂ β ， α ∩ β ＝ b ⇒ a ∥ b 一条直线与此平面内 的一条直线 交线 2. 平面与平面平行 (1) 平面与平面平行的定义 没有公共点的两个平面叫做平行平面 . (2) 判定定理与性质定理   文字语言 图形表示 符号表示 判定定理 一个平面内的两 条 与 另一个平面平行，则这两个平面平行 a ⊂ α ， b ⊂ α ， a ∩ b ＝ P ， a ∥ β ， b ∥ β ⇒ α ∥ β 相交直线 性质定理 两个平面平行，则其中一个平面内的 直线 于 另一个平面 α ∥ β ， a ⊂ α ⇒ a ∥ β 如果两个平行平面同时和第三个平面相交，那么它们 的 平行 α ∥ β ， α ∩ γ ＝ a ， β ∩ γ ＝ b ⇒ a ∥ b 平行 交线 3. 与垂直相关的平行的判定 (1) a ⊥ α ， b ⊥ α ⇒ . (2) a ⊥ α ， a ⊥ β ⇒ . a ∥ b α ∥ β [ 常用结论与易错提醒 ] 1. 平行关系的转化 2. 平面与平面平行的六个性质 (1) 两个平面平行，其中一个平面内的任意一条直线平行于另一个平面 . (2) 夹在两个平行平面间的平行线段长度相等 . (3) 经过平面外一点有且只有一个平面与已知平面平行 . (4) 两条直线被三个平行平面所截，截得的对应线段成比例 . (5) 如果两个平面分别和第三个平面平行，那么这两个平面互相平行 . (6) 如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线，那么这两个平面平行 . 诊 断 自 测 1. 判断下列说法的正误 . (1) 若一条直线和平面内一条直线平行，那么这条直线和这个平面平行 .( 　　 ) (2) 若直线 a ∥ 平面 α ， P ∈ α ，则过点 P 且平行于直线 a 的直线有无数条 .( 　　 ) (3) 如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行 .( 　　 ) (4) 如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面 .( 　　 ) 解析　 (1) 若一条直线和平面内的一条直线平行，那么这条直线和这个平面平行或在平面内，故 (1) 错误 . (2) 若 a ∥ α ， P ∈ α ，则过点 P 且平行于 a 的直线只有一条，故 (2) 错误 . (3) 如果一个平面内的两条直线平行于另一个平面，则这两个平面平行或相交，故 (3) 错误 . 答案　 (1) × 　 (2) × 　 (3) × 　 (4) √ 2. (2018· 浙江卷 ) 已知平面 α ，直线 m ， n 满足 m ⊄ α ， n ⊂ α ，则 “ m ∥ n ” 是 “ m ∥ α ” 的 ( 　　 ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 解析 　若 m ⊄ α ， n ⊂ α ， m ∥ n ，由线面平行的判定定理知 m ∥ α . 若 m ∥ α ， m ⊄ α ， n ⊂ α ，不一定推出 m ∥ n ，直线 m 与 n 可能异面，故 “ m ∥ n ” 是 “ m ∥ α ” 的充分不必要条件 . 故选 A. 答案 　 A 3. 下列命题中正确的是 ( 　　 ) A. 若 a ， b 是两条直线，且 a ∥ b ，那么 a 平行于经过 b 的任何平面 B. 若直线 a 和平面 α 满足 a ∥ α ，那么 a 与 α 内的任何直线平行 C. 若直线 a ， b 和平面 α 满足 a ∥ α ， b ∥ α ，那么 a ∥ b D. 若直线 a ， b 和平面 α 满足 a ∥ b ， a ∥ α ， b ⊄ α ，则 b ∥ α 解析 　根据线面平行的判定与性质定理知，选 D. 答案 　 D 4. ( 必修 2P56 练习 2 改编 ) 如图，正方体 ABCD － A 1 B 1 C 1 D 1 中， E 为 DD 1 的中点，则 BD 1 与平面 AEC 的位置关系为 ________. 解析　 连接 BD ，设 BD ∩ AC ＝ O ，连接 EO ，在 △ BDD 1 中， O 为 BD 的中点， E 为 DD 1 的中点，所以 EO 为 △ BDD 1 的中位线，则 BD 1 ∥ EO ，而 BD 1 ⊄ 平面 ACE ， EO ⊂ 平面 ACE ，所以 BD 1 ∥ 平面 ACE . 答案　 平行 5. 用一 个截面去截正三棱柱 ABC － A 1 B 1 C 1 ，交 A 1 C 1 ， B 1 C 1 ， BC ， AC 分别于 E ， F ， G ， H 四点，已知 A 1 A > A 1 C 1 ，则截面的形状可以是 ________( 把你认为可能的结果都填上 ). 解析　 由题意知，当截面平行于侧棱时所得截面为矩形，当截面与侧棱不平行时，所得的截面是梯形 . 答案 　矩形或梯形 6. 设 α ， β ， γ 为三个不同的平面， a ， b 为直线 . (1) 若 α ∥ γ ， β ∥ γ ，则 α 与 β 的关系是 ________ ； (2) 若 a ⊥ α ， b ⊥ β ， a ∥ b ，则 α 与 β 的关系是 ________. 解析 　 (1) 由 α ∥ γ ， β ∥ γ ⇒ α ∥ β . (2) a ⊥ α ， a ∥ b ⇒ b ⊥ α ，又 b ⊥ β ，从而 α ∥ β . 答案　 (1) 平行　 (2) 平行 考点一　线面、面面平行的相关命题的真假判断 【例 1 】 (1) (2019· 全国 Ⅱ 卷 ) 设 α ， β 为两个平面，则 α ∥ β 的充要条件是 ( 　　 ) A. α 内有无数条直线与 β 平行 B. α 内有两条相交直线与 β 平行 C. α ， β 平行于同一条直线 D. α ， β 垂直于同一平面 (2) ( 一题多解 ) 如图，在下列四个正方体中， A ， B 为正方体的两个顶点， M ， N ， Q 为所在棱的中点，则在这四个正方体中，直线 AB 与平面 MNQ 不平行的是 ( 　　 ) 解析 　 (1) 若 α ∥ β ，则 α 内有无数条直线与 β 平行，当无数条直线互相平行时， α 与 β 可能相交；若 α ， β 平行于同一条直线，则 α 与 β 可以平行也可以相交；若 α ， β 垂直于同一个平面，则 α 与 β 可以平行也可以相交，故 A ， C ， D 中条件均不是 α ∥ β 的充要条件 . 根据两平面平行的判定定理知，若一个平面内有两条相交直线与另一个平面平行，则两平面平行，反之也成立 . 因此 B 中条件是 α ∥ β 的充要条件 . (2) 法一 　对于选项 B ，如图 (1) 所示，连接 CD ，因为 AB ∥ CD ， M ， Q 分别是所在棱的中点，所以 MQ ∥ CD ，所以 AB ∥ MQ ，又 AB ⊄ 平面 MNQ ， MQ ⊂ 平面 MNQ ，所以 AB ∥ 平面 MNQ . 同理可证选项 C ， D 中均有 AB ∥ 平面 MNQ . 因此 A 项不正确 . 图 (1) 图 (2) 法二　 对于选项 A ，其中 O 为 BC 的中点 ( 如图 (2) 所示 ) ，连接 OQ ，则 OQ ∥ AB ，因为 OQ 与平面 MNQ 有交点，所以 AB 与平面 MNQ 有交点，即 AB 与平面 MNQ 不平行 .A 项不正确 . 答案 　 (1)B 　 (2)A 规律方法 　 (1) 判断与平行关系相关命题的真假，必须熟悉线、面平行关系的各个定义、定理，无论是单项选择还是含选择项的填空题，都可以从中先选出最熟悉最容易判断的选项先确定或排除，再逐步判断其余选项 . (2) ① 结合题意构造或绘制图形，结合图形作出判断 . ② 特别注意定理所要求的条件是否完备，图形是否有特殊情况，通过举反例否定结论或用反证法推断命题是否正确 . 【训练 1 】 (1) (2020· 杭州质检 ) 已知三个不同的平面 α ， β ， γ 和直线 m ， n ，若 α ∩ γ ＝ m ， β ∩ γ ＝ n ，则 “ α ∥ β ” 是 “ m ∥ n ” 的 ( 　　 ) A. 充分不必要条件 B . 必要不充分条件 C. 充要条件 D . 既不充分也不必要条件 (2) 设 m ， n 是两条不同的直线， α ， β ， γ 是三个不同的平面，给出下列四个命题： ① 若 m ⊂ α ， n ∥ α ，则 m ∥ n ； ② 若 α ∥ β ， β ∥ γ ， m ⊥ α ，则 m ⊥ γ ； ③ 若 α ∩ β ＝ n ， m ∥ n ， m ∥ α ，则 m ∥ β ； ④ 若 m ∥ α ， n ∥ β ， m ∥ n ，则 α ∥ β . 其中是真命题的是 ________( 填上正确命题的序号 ). 解析 　 (1) 可知当 “ α ∥ β ” 时有 “ m ∥ n ” ，反之，不一定成立，则 “ α ∥ β ” 是 “ m ∥ n ” 的充分不必要条件，故选 A. (2) ① m ∥ n 或 m ， n 异面，故 ① 错误；易知 ② 正确； ③ m ∥ β 或 m ⊂ β ，故 ③ 错误； ④ α ∥ β 或 α 与 β 相交，故 ④ 错误 . 答案 　 (1)A 　 (2) ② 考点二　直线与平面平行的判定与性质 角度 1 　直线与平面平行的判定 【例 2 － 1 】 如图，四棱锥 P － ABCD 中， PA ⊥ 底面 ABCD ， AD ∥ BC ， AB ＝ AD ＝ AC ＝ 3 ， PA ＝ BC ＝ 4 ， M 为线段 AD 上一点， AM ＝ 2 MD ， N 为 PC 的中点 . 多维探究 (1) 证明： MN ∥ 平面 PAB ； (2) 求四面体 N － BCM 的体积 . 又 AD ∥ BC ，故 TN 綉 AM ，所以四边形 AMNT 为平行四边形，于是 MN ∥ AT . 因为 AT ⊂ 平面 PAB ， MN ⊄ 平面 PAB ， 所以 MN ∥ 平面 PAB . (1) 证明： GH ∥ EF ； (2) 若 EB ＝ 2 ，求四边形 GEFH 的面积 . (1) 证明　 因为 BC ∥ 平面 GEFH ， BC ⊂ 平面 PBC ，且平面 PBC ∩ 平面 GEFH ＝ GH ， 所以 GH ∥ BC . 同理可证 EF ∥ BC ，因此 GH ∥ EF . (2) 解　 如图，连接 AC ， BD 交于点 O ， BD 交 EF 于点 K ，连接 OP ， GK . 因为 PA ＝ PC ， O 是 AC 的中点，所以 PO ⊥ AC ， 同理可得 PO ⊥ BD . 又 BD ∩ AC ＝ O ，且 AC ， BD 都在底面 ABCD 内，所以 PO ⊥ 底面 ABCD . 又因为平面 GEFH ⊥ 平面 ABCD ， 且 PO ⊄ 平面 GEFH ，所以 PO ∥ 平面 GEFH . 因为平面 PBD ∩ 平面 GEFH ＝ GK ， PO ⊂ 平面 PBD . 所以 PO ∥ GK ，且 GK ⊥ 底面 ABCD ，又 EF ⊂ 平面 ABCD ，从而 GK ⊥ EF . 所以 GK 是梯形 GEFH 的高 . 由 AB ＝ 8 ， EB ＝ 2 及 EK ∥ AD ，得 EB ∶ AB ＝ KB ∶ DB ＝ 1 ∶ 4 ， 规律方法　 (1) 判断或证明线面平行的常用方法有： ① 利用反证法 ( 线面平行的定义 ) ； ② 利用线面平行的判定定理 ( a ⊄ α ， b ⊂ α ， a ∥ b ⇒ a ∥ α ) ； ③ 利用面面平行的性质定理 ( α ∥ β ， a ⊂ α ⇒ a ∥ β ) ； ④ 利用面面平行的性质 ( α ∥ β ， a ⊄ β ， a ∥ α ⇒ a ∥ β ). (2) 利用判定定理判定线面平行，关键是找平面内与已知直线平行的直线 . 常利用三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线 . (1) 求证： AP ∥ 平面 BEF ； (2) 求证： GH ∥ 平面 PAD . ∴ 四边形 ABCE 是平行四边形， ∴ O 为 AC 的中点， 又 ∵ F 是 PC 的中点， ∴ FO ∥ AP ， 又 FO ⊂ 平面 BEF ， AP ⊄ 平面 BEF ， ∴ AP ∥ 平面 BEF . (2) 连接 FH ， OH ， ∵ F ， H 分别是 PC ， CD 的中点， ∴ FH ∥ PD ，又 PD ⊂ 平面 PAD ， FH ⊄ 平面 PAD ， ∴ FH ∥ 平面 PAD . 又 ∵ O 是 BE 的中点， H 是 CD 的中点， ∴ OH ∥ AD ，又 ∵ AD ⊂ 平面 PAD ， OH ⊄ 平面 PAD ， ∴ OH ∥ 平面 PAD . 又 FH ∩ OH ＝ H ， ∴ 平面 OHF ∥ 平面 PAD . 又 ∵ GH ⊂ 平面 OHF ， ∴ GH ∥ 平面 PAD . 考点三　面面平行的判定与性质 【例 3 】 ( 经典母题 ) 如图所示， 在三棱柱 ABC － A 1 B 1 C 1 中， E ， F ， G ， H 分别是 AB ， AC ， A 1 B 1 ， A 1 C 1 的中点，求证： (1) B ， C ， H ， G 四点共面； (2) 平面 EFA 1 ∥ 平面 BCHG . 证明 　 (1) ∵ G ， H 分别是 A 1 B 1 ， A 1 C 1 的中点， ∴ GH 是 △ A 1 B 1 C 1 的中位线，则 GH ∥ B 1 C 1 . 又 ∵ B 1 C 1 ∥ BC ， ∴ GH ∥ BC ， ∴ B ， C ， H ， G 四点共面 . 变式迁移 (2) ∵ E ， F 分别为 AB ， AC 的中点， ∴ EF ∥ BC ， ∵ EF ⊄ 平面 BCHG ， BC ⊂ 平面 BCHG ， ∴ EF ∥ 平面 BCHG . 又 G ， E 分别为 A 1 B 1 ， AB 的中点， A 1 B 1 綉 AB ， ∴ A 1 G 綉 EB ， ∴ 四边形 A 1 EBG 是平行四边形， ∴ A 1 E ∥ GB . ∵ A 1 E ⊄ 平面 BCHG ， GB ⊂ 平面 BCHG ， ∴ A 1 E ∥ 平面 BCHG . 又 ∵ A 1 E ∩ EF ＝ E ， ∴ 平面 EFA 1 ∥ 平面 BCHG . 【变式迁移 1 】 如图，在本例条件下，若点 D 为 BC 1 的中点，求证： HD ∥ 平面 A 1 B 1 BA . 证明　 如图 所示，连接 A 1 B . ∵ D 为 BC 1 的中点， H 为 A 1 C 1 的中点， ∴ HD ∥ A 1 B ， 又 HD ⊄平面 A 1 B 1 BA ， A 1 B ⊂ 平面 A 1 B 1 BA ， ∴ HD ∥ 平面 A 1 B 1 BA . 解　 连接 A 1 B 交 AB 1 于 O ，连接 OD 1 . 规律方法　 (1) 判定面面平行的主要方法 ① 利用面面平行的判定定理 . ② 线面垂直的性质 ( 垂直于同一直线的两平面平行 ). (2) 面面平行的性质定理 ① 两平面平行，则一个平面内的直线平行于另一平面 . ② 若一平面与两平行平面相交，则交线平行 . 提醒 　利用面面平行的判定定理证明两平面平行时需要说明是一个平面内的两条相交直线与另一个平面平行 . 【训练 3 】 在如图所示的几何体中， D 是 AC 的中点， EF ∥ DB . (1) 已知 AB ＝ BC ， AE ＝ EC . 求证： AC ⊥ FB ； (2) 已知 G ， H 分别是 EC 和 FB 的中点 . 求证： GH ∥ 平面 ABC . 证明　 (1) 因为 EF ∥ DB ，所以 EF 与 DB 确定平面 BDEF ， 如图 ① ，连接 DE . 因为 AE ＝ EC ， D 为 AC 的中点， 图 ① 所以 DE ⊥ AC . 同理可得 BD ⊥ AC . 又 BD ∩ DE ＝ D ， 所以 AC ⊥ 平面 BDEF . 因为 FB ⊂ 平面 BDEF ， 所以 AC ⊥ FB . (2) 如图 ② ，设 FC 的中点为 I ，连接 GI ， HI . 在 △ CEF 中，因为 G 是 CE 的中点， 所以 GI ∥ EF . 又 EF ∥ DB ， 所以 GI ∥ DB . 图 ② 在 △ CFB 中，因为 H 是 FB 的中点，所以 HI ∥ BC . 又 HI ∩ GI ＝ I ， 所以平面 GHI ∥ 平面 ABC ， 因为 GH ⊂ 平面 GHI ， 所以 GH ∥ 平面 ABC .