2020_2021学年新教材高中数学第二章直线和圆的方程2

2020_2021学年新教材高中数学第二章直线和圆的方程2

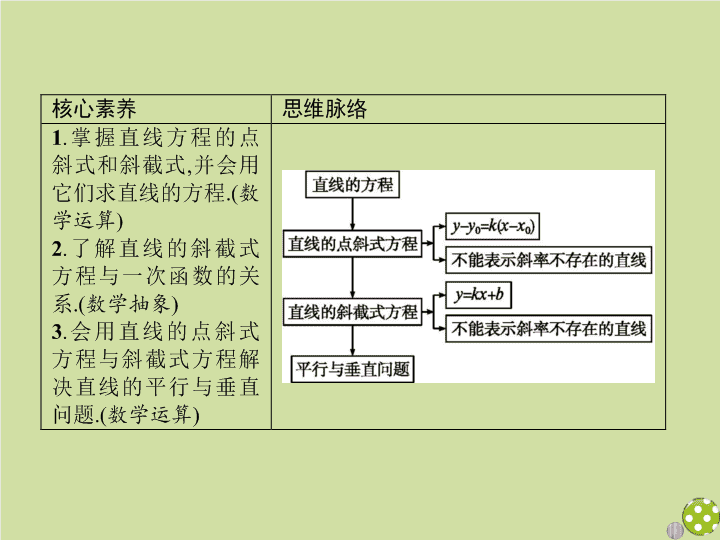
2.2.1 　直线的点斜式方程 激趣诱思 知识点拨 在平面直角坐标系中 , 直线 l 过点 P (0,3), 斜率 k=- 2, Q ( x , y ) 是直线 l 上不同于 P 的任意一点 , 如图所示 . 由于 P , Q 都在 l 上 , 所以可以用 P , Q 的坐标来表示直线 l 的斜率 , = 2, 即得方程 y= 2 x+ 3 . 这表明直线 l 上任一点的坐标 ( x , y ) 都满足 y= 2 x+ 3 . 那么满足方程 y= 2 x+ 3 的每一组 ( x , y ) 所对应的点也都在直线 l 上吗 ? 激趣诱思 知识点拨 一、直线的点斜式 方程 名师点析 1 . 点斜式应用的前提是直线的斜率存在 , 若斜率不存在 , 则不能应用此式 . 2 . 点斜式方程中的点只要是这条直线上的点 , 哪一个都可以 . 3 . 当直线与 x 轴平行或重合时 , 方程可简写为 y=y 0 . 特别地 , x 轴的方程是 y= 0; 当直线与 y 轴平行或重合时 , 不能应用点斜式方程 . 此时可将方程写成 x=x 0 . 特别地 , y 轴的方程是 x= 0 . 激趣诱思 知识点拨 微练习 直线 l 的点斜式方程是 y- 2 = 3( x+ 1), 则直线 l 的斜率是 ( 　　 ) A.2 　　　　　　　　　 B.-1 C.3 D .-3 答案 : C 答案 : 不一样 . 后者表示过点 ( x 0 , y 0 ) 且斜率为 k 的一条直线 , 前者是这条直线上挖去了一个点 ( x 0 , y 0 ) . 激趣诱思 知识点拨 二、直线的斜截式 方程 名师点析 1 . 直线的斜截式方程是直线的点斜式方程的特殊情况 . 2 . 截距是一个实数 , 它是直线与坐标轴交点的横坐标或纵坐标 , 可以为正数、负数和 0 . 当直线过原点时 , 它的横截距和纵截距都为 0 . 3 . 由直线的斜截式方程可直接得到直线的斜率和纵截距 , 如直线 y= 2 x- 1 的斜率 k= 2, 纵截距为 - 1 . 激趣诱思 知识点拨 微练习 直线 l 的斜截式方程是 y=- 2 x+ 3, 则直线 l 在 y 轴上的截距为 　　　　　 .   答案 : 3 微思考 一次函数的解析式 y=kx+b 与直线的斜截式方程 y=kx+b 有什么不同 ? 答案 : 一次函数的 x 的系数 k ≠0, 否则就不是一次函数了 ; 直线的斜截式方程 y=kx+b 中的 k 可以为 0 . 激趣诱思 知识点拨 三、根据直线的斜截式方程判断两直线平行与垂直 对于直线 l 1 : y=k 1 x+b 1 , l 2 : y=k 2 x+b 2 , l 1 ∥ l 2 ⇔ k 1 =k 2 , 且 b 1 ≠ b 2 ; l 1 ⊥ l 2 ⇔ k 1 k 2 =- 1 . 名师点析 两直线的斜率之积为 - 1, 则两直线一定垂直 ; 两条直线的斜率相等 , 两直线不一定平行 , 还可能重合 . 微练习 已知直线 l 1 : y=x+ 2 与 l 2 : y=- 2 ax+ 1 平行 , 则 a= 　　　　　 .   探究一 探究二 当堂检测 直线的点斜式方程 例 1 求满足下列条件的直线方程 : (1) 经过点 (2, - 3), 倾斜角是直线 y = x 倾斜角的 2 倍 ; (2) 经过点 P (5, - 2), 且与 y 轴平行 ; (3) 过 P ( - 2,3), Q (5, - 4) 两点 . 思路分析 : 先求出直线的斜率 , 然后由点斜式写出方程 . 探究一 探究二 当堂检测 (2) 与 y 轴平行的直线 , 其斜率 k 不存在 , 不能用点斜式方程表示 . 但直线上点的横坐标均为 5, 故直线方程可记为 x= 5 . ∵ 直线过点 P ( - 2,3), ∴ 由直线的点斜式方程可得直线方程为 y- 3 =- ( x+ 2), 即 x+y- 1 = 0 . 探究一 探究二 当堂检测 反思感悟 点斜式方程的求法 (1) 求直线的点斜式方程 , 关键是求出直线的斜率 , 所以 , 已知直线上一点的坐标及直线的斜率或直线上两点坐标 , 均可求出直线的方程 . (2) 斜率不存在时 , 可直接写出过点 ( x 0 , y 0 ) 的直线方程 x=x 0 . 探究一 探究二 当堂检测 变式训练 1 直线 l 1 的倾斜角为 135 ° , 直线 l 2 经过点 B ( - 1,4) . 求满足下列条件的直线 l 2 的方程 . (1) 直线 l 2 ∥ l 1 ; (2) 直线 l 2 ⊥ l 1 . 解 : (1) 由已知直线 l 1 的斜率 k 1 = tan 135 ° =- 1 . 因为 l 2 ∥ l 1 , 所以直线 l 2 的斜率 k 2 =k 1 =- 1 . 又直线 l 2 经过点 B ( - 1,4), 代入点斜式方程得 y- 4 =- 1 × [ x- ( - 1)], 即 y=-x+ 3 . (2) 由已知直线 l 1 的斜率 k 1 = tan 135 ° =- 1 . 又直线 l 2 经过点 B ( - 1,4), 代入点斜式方程得 y- 4 = 1 × [ x- ( - 1)], 即 y=x+ 5 . 探究一 探究二 当堂检测 直线的斜截式方程 例 2 求满足下列条件的直线方程 : (1) 经过点 (0, - 2), 且与直线 y= 3 x- 5 垂直 ; (2) 与直线 y=- 2 x+ 3 平行 , 与直线 y= 4 x- 2 在 y 轴上的截距相同 . 思路分析 : 写出直线的斜率及在 y 轴上的截距 , 用斜截式写出直线方程 . 解 : (1) 因为直线 y= 3 x- 5 的斜率为 3, 且所求直线与该直线垂直 , 所以所求直线斜率为 - . 又直线过点 (0, - 2), 由直线方程的斜截式 , 得 y=- x- 2 , 即 x+ 3 y+ 6 = 0 . (2) 直线 y=- 2 x+ 3 的斜率为 - 2, 直线 y= 4 x- 2 在 y 轴上的截距为 - 2 . 由题意知 , 所求直线的斜率为 - 2, 在 y 轴上的截距也为 - 2 . 由直线方程的斜截式 , 得 y=- 2 x- 2, 即 2 x+y+ 2 = 0 . 探究一 探究二 当堂检测 反思感悟 斜截式方程的求法 已知直线的斜率与 y 轴上的截距 , 可直接写出直线的方程 ; 已知直线的斜截式方程 , 可得直线的斜率与 y 轴上的截距 . 直线的斜截式方程形式简单 , 特点明显 , 是运用较多的直线方程的形式之一 . 探究一 探究二 当堂检测 探究一 探究二 当堂检测 1 . 与直线 y= 3 x+ 1 垂直 , 且过点 (2, - 1) 的直线的斜截式方程是 ( 　　 ) 答案 : B 2 . 无论 k 取何值 , 直线 y- 2 =k ( x+ 1) 所过的定点是 　　　　 .   答案 : ( - 1,2) 3 . 直线 l 的倾斜角为 45 ° , 在 y 轴上的截距为 - 2 的直线方程为 　　　　　 .   答案 : y=x- 2 探究一 探究二 当堂检测 4 . 直线 l 1 与直线 l 2 : y= 3 x+ 1 平行 , 又直线 l 1 过点 (3,5), 则直线 l 1 的方程为 　　　　　　 .   解析 : ∵ 直线 l 2 的斜率 k 2 = 3, l 1 与 l 2 平行 , ∴ 直线 l 1 的斜率 k 1 = 3 . 又直线 l 1 过点 (3,5), ∴ l 1 的方程为 y- 5 = 3( x- 3), 即 y= 3 x- 4 . 答案 : y= 3 x- 4