- 2021-07-01 发布 |
- 37.5 KB |
- 27页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江苏省宿迁市2020届高三下学期5月联考数学试题 Word版含解析
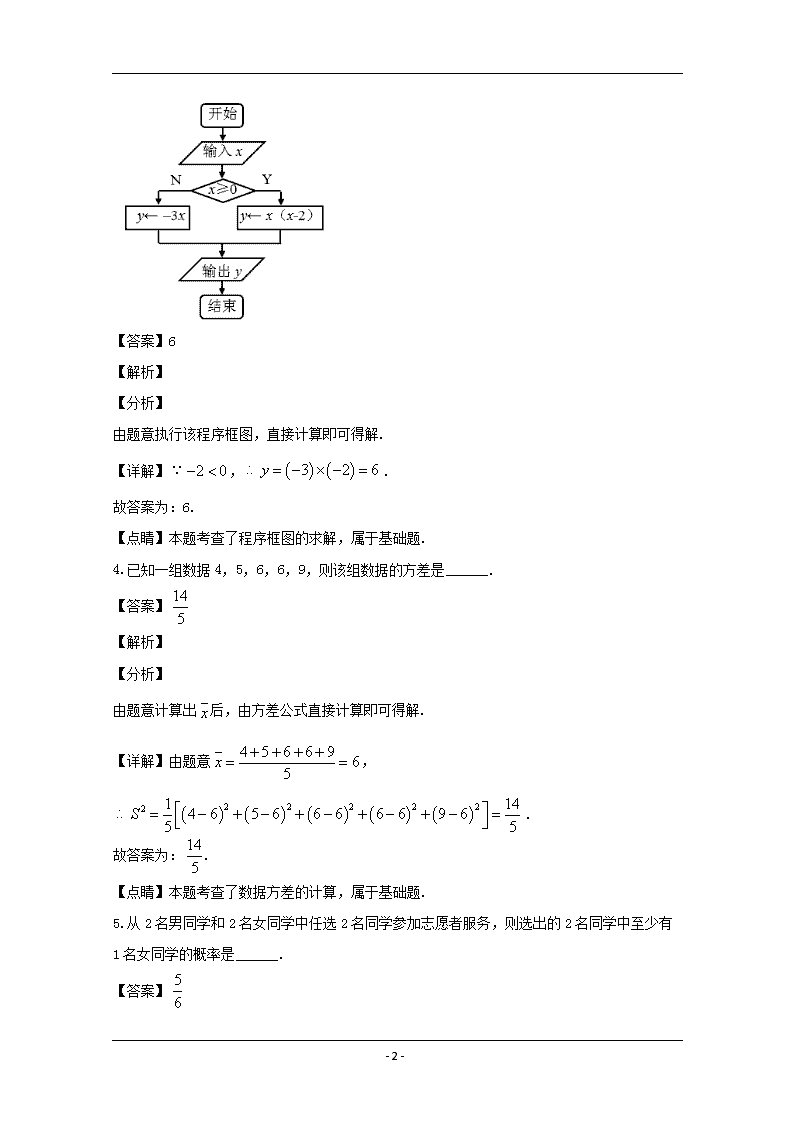
- 1 - 江苏省宿迁市 2019~2020 学年度第二学期高三年级 5 月联考 数学试题 第Ⅰ卷(必做题,共 160 分) 一、填空题(请将答案填写在答题卷相应的位置上.) 1.已知集合 0A x x , 1,0,1,2B ,则 A B 等于 . 【答案】 1,2 【解析】 试题分析: | 0 1,0,1,2 1,2A B x x 考点:集合运算 【方法点睛】 1.用描述法表示集合,首先要弄清集合中代表元素的含义,再看元素的限制条件,明确集合 类型,是数集、点集还是其他的集合. 2.求集合的交、并、补时,一般先化简集合,再由交、并、补的定义求解. 3.在进行集合的运算时要尽可能地借助 Venn 图和数轴使抽象问题直观化.一般地,集合元 素离散时用 Venn 图表示;集合元素连续时用数轴表示,用数轴表示时要注意端点值的取舍. 2.若复数 z 满足 2 4iz i (i 是虚数单位),则复数 z 的模等于______. 【答案】 2 5 【解析】 【分析】 由题意可得 2 4 4 2iz ii ,再由复数模的概念即可得解. 【详解】复数 z 满足 2 4iz i , 2 2 2 4 2 4 4 2i i iz ii i , 224 2 2 5z . 故答案为: 2 5 . 【点睛】本题考查了复数的运算与复数模的求解,属于基础题. 3.如图所示,运行该流程图,若输入值 2x ,则输出的 y 值为______. - 2 - 【答案】6 【解析】 【分析】 由题意执行该程序框图,直接计算即可得解. 【详解】 2 0 , 3 2 6y . 故答案为:6. 【点睛】本题考查了程序框图的求解,属于基础题. 4.已知一组数据 4,5,6,6,9,则该组数据的方差是______. 【答案】 14 5 【解析】 【分析】 由题意计算出 x 后,由方差公式直接计算即可得解. 【详解】由题意 4 5 6 6 9 65x , 2 2 2 2 22 1 144 6 5 6 6 6 6 6 9 65 5S . 故答案为:14 5 . 【点睛】本题考查了数据方差的计算,属于基础题. 5.从 2 名男同学和 2 名女同学中任选 2 名同学参加志愿者服务,则选出的 2 名同学中至少有 1 名女同学的概率是______. 【答案】 5 6 - 3 - 【解析】 【分析】 由题意分别计算出所有情况数与符合要求的情况数,再结合古典概型概率公式即可得解. 【详解】从 2 名男同学和 2 名女同学中任选 2 名同学共有 2 4 6C 种情况, 其中 2 名同学中至少有 1 名女同学有 1 1 2 2 2 2 5C C C 种情况, 故所求概率 5 6P . 故答案为: 5 6 . 【点睛】本题考查了计数原理的应用及古典概型概率的求解,属于基础题. 6.过双曲线 2 2 13 x y 的右焦点且与 x 轴垂直的直线,交该双曲线的两条渐近线于 A , B 两 点,则 AB 的长度为______. 【答案】 4 3 3 【解析】 【分析】 由题意求得双曲线的渐近线方程与右焦点,进而可得点 32, 2 3A , 32, 2 3B ,即可得 解. 【详解】双曲线 2 2 13 x y 的渐近线方程为 3 3y x ,右焦点为 2,0 , 则点 32, 2 3A , 32, 2 3B , 所以 2 3 2 3 4 3 3 3 3AB . 故答案为: 4 3 3 . 【点睛】本题考查了双曲线性质的简单应用,属于基础题. 7.已知等差数列 na 中, 1 3a , 5 811 5a a ,则其前 n 项和 nS 的最小值为______. - 4 - 【答案】﹣4 【解析】 【分析】 由题意结合等差数列的通项公式可得 11 3 4 5 3 7d d ,求出 2d 后,可得 22 4nS n ,即可得解. 【详解】设等差数列 na 的公差为 d , 5 811 5a a , 1 3a , 11 3 4 5 3 7d d ,解得 2d , 213 2 2 42n n nS n n , 当 2n 时, nS 的最小值为 4 . 故答案为: 4 . 【点睛】本题考查了等差数列基本量运算与前 n 项和最值的求解,属于基础题. 8.已知函数 ( ) sinf x x 0 4 的图象向左平移 12 个单位后,关于点 5 ,012 对称, 则实数 的值为______. 【答案】2 【解析】 【分析】 由题意平移之后的函数为 sin 12g x x ,进而可得 5 12 12 k , k Z , 即可得解. 【详解】设函数 ( ) sinf x x 的图象向左平移 12 个单位后得 sin 12g x x 的图 象, 由题意 sin 12g x x 关于点 5 ,012 对称, ∴ 5 12 12 k , k Z , - 5 - ∴ 2k , k Z , 0 4 , 2 . 故答案为:2. 【点睛】本题考查了三角函数图象的平移与对称性的应用,属于基础题. 9.已知圆锥的底面直径与母线长相等,一球体与该圆锥的所有母线和底面都相切,记圆锥和 球体的体积分别为 1V , 2V ,则 1 2 V V 的值为______. 【答案】 9 4 【解析】 【分析】 设圆锥底面半径为 R ,圆锥的内切球半径为 r ,由题意画出圆锥轴截面图,进而可得 3 3r R 、 圆锥高 3h R= ,即可得解. 【详解】设圆锥底面半径为 R ,圆锥的内切球半径为 r , 由题意知,圆锥的轴截面是边长为 2R 的正三角形,球的大圆为该正三角形的内切圆,如图, 3 3r R ,圆锥高 3h R= , 2 1 3 2 1 3 93 44 3 3 3 R RV V R . 故答案为: 9 4 . 【点睛】本题考查了圆锥几何特征的应用及其内切圆相关问题的求解,属于基础题. - 6 - 10.已知 是第二象限角,且 4sin 5 ,则 tan 2 4 的值为______. 【答案】 1 3 【解析】 【分析】 由题意结合同角三角函数的关系可得 4tan 3 ,根据二倍角的正切公式可得 tan 22 ,最 后利用两角差的正切公式即可得解. 【详解】 是第二象限角,且 4sin 5 , 2 , 2 ,2 k k k Z , 2 3cos 1 sin 5 , sin 4tan cos 3 , 2 2tan 42tan tan 2 2 31 tan 2 , 又 , ,2 4 2k k k Z Î + + Î , θtan 02 > ,解得 tan 22 , tan 1 2 1 12tan 2 4 1 2 31 tan 2 . 故答案为: 1 3 . 【点睛】本题考查了两角差的正切公式及二倍角的正切公式的应用,考查了同角三角函数关 系的应用和运算能力,属于中档题. 11.设 1 2 1log 1 2 bxf x x 是定义在区间 ( , )a a 上的奇函数,且为单调函数,则 ab 的取值范围 是______. 【答案】1, 2 【解析】 【分析】 - 7 - 由题意结合奇函数的性质可得 2 4b ,由函数单调性可得 2b ,求得函数 f x 的定义域后 即可得 10 2a ,再由指数函数的性质即可得解. 【详解】 1 2 1log 1 2 bxf x x 是定义在区间 ,a a 上的奇函数, 0f x f x ,即 1 1 2 2 1 1log log 01 2 1 2 bx bx x x , 1 1 11 2 1 2 bx bx x x 得 2 4b , 又 f x 为单调函数, 2b , 1 2 1 2log 1 2 xf x x , 令1 2 01 2 x x 即 1 2 1 2 0x x ,则 1 1 2 2x , 10 2a , 2 1, 2a ab . 故答案为:1, 2 . 【点睛】本题考查了指数函数、对数函数的图象与性质的应用,考查了函数奇偶性的应用, 属于中档题. 12.在 ABC 中, 4AB , 2AC , 60BAC ,已知点 E , F 分别是边 AB , AC 的 中点,点 D 在边 BC 上.若 13 4DE DF ,则线段 BD 的长为______. 【答案】 3 2 【解析】 【分析】 由题意结合余弦定理可得 2 12BC ,即可得 90C ,建立平面直角坐标系后,表示出各点 坐标,由 13 4DE DF 转化为坐标运算即可得解. 【详解】在 ABC 中, 4AB , 2AC , 60BAC , 则 2 2 2 2 cos 16 4 8 12BC AC AB AC AB BAC , 2 2 2BC AC AB , 90C , - 8 - 以C 为坐标原点,点 A 、 B 分别在 x 轴、 y 轴正半轴上建立平面直角坐标系,如图, 则 0,0C , 2,0A , 0,2 3B , 1, 3E , 1,0F , 设 0, 0 2 3D d d , 故 1, 3DE d , 1,DF d , 13 4DE DF , 2 131 3 4d d ,解得 3 3 2d 或 3 2d (舍去), 3 3 32 3 2 2BD . 故答案为: 3 2 . 【点睛】本题考查了余弦定理与平面向量数量积的坐标运算,考查了运算求解能力,属于基 础题 13.在平面直角坐标系中, A ,B 分别是 x 轴和 y 轴上的动点,若以 AB 为直径的圆C 与直线 2 10 0x y 相切,当圆 C 面积最小时,圆 C 的标准方程为______. 【答案】 2 22 1 5x y 【解析】 【分析】 由题意易知原点O 在圆C 上,作 OD 垂直直线 2 10 0x y 于点 D ,进而可得当 OD 为圆C 直径时,圆C 面积最小,求出直线 : 2 0OD x y 后,联立方程即可得点 4,2D ,求得圆的 圆心与半径后即可得解. - 9 - 【详解】由题意可得,原点 O 在圆C 上, 作OD 垂直直线 2 10 0x y 于点 D , 则当 OD 为圆C 直径时,圆C 面积最小, 易知 1 2ODk ,所以直线 : 2 0OD x y , 由 2 0 2 10 0 x y x y 可得点 4,2D ,所以 2,1C ,半径 4 1 5OC , 故圆C 的方程为 2 22 1 5x y . 故答案为: 2 22 1 5x y . 【点睛】本题考查了直线与圆的综合问题,考查了运算求解能力与转化化归思想,属于中档 题. 14.函数 f(x) 2 1 x ax x x a , , > ,若任意 t∈(a﹣1,a),使得 f(t)>f(t+1),则实数 a 的取值范围为______. 【答案】1 3 a 2 1 【解析】 【分析】 根据 f(x) 2 1 x ax x x a , , > ,由 t∈(a﹣1,a)⇒t+1∈(a,a+1),得到 f(t) 2 1t ; f(t+1)=|t+1|;再根据任意 t∈(a﹣1,a),使得 f(t)>f(t+1),即 2 1t >|t+1|⇒|t+1| (|t|+1)﹣2<0;然后分当 t>0,﹣1≤t≤0,t<﹣1 时,解不等式得 3 <t 2 < 1; 根据若任意 t∈(a﹣1,a),使得 f(t)>f(t+1)成立,则(a﹣1,a)是( 3, 2 1) 的子集求解. 【详解】因为:f(x) 2 1 x ax x x a , , > , - 10 - 由 t∈(a﹣1,a)⇒t+1∈(a,a+1), ∴f(t) 2 1t ;f(t+1)=|t+1|; ∵任意 t∈(a﹣1,a),使得 f(t)>f(t+1), ∴ 2 1t >|t+1|⇒ 1 1 2 0t t ;① 当 t>0 时,①式转化为 1 1 2 0t t ⇒0<t 2 1< ; 当 1 0t 时①式转化为 1 1 2 0t t ⇒ 21 2 0t ,∴ 1 0t ; t<﹣1 时①式转化为 1 1 2 0t t ⇒t2﹣3<0⇒ 3 <t<0; 综上可得 3 <t 2 < 1; ∵若任意 t∈(a﹣1,a),使得 f(t)>f(t+1), ∴a﹣1 3 且 a 2 1; ∴1 3 a 2 1; 【点睛】本题主要考查绝对值不等式的解法和集合关系的应用,还考查了分类讨论的思想和 运算求解的能力,属于中档题. 二、解答题(请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.) 15.如图,在四棱锥 P ABCD 中,底面 ABCD 是直角梯形,且 / /AD BC , AB BC , 2BC AD ,已知平面 PAB 平面 ABCD , E , F 分别为 BC , PC 的中点.求证: (1) / /AB 平面 DEF ; (2) BC ⊥平面 DEF . 【答案】(1)详见解析;(2)详见解析. 【解析】 - 11 - 【分析】 (1)由题意可得四边形 ADEB 是平行四边形,即可得 / /AB DE ,再根据线面平行的判定即 可得证; (2)由面面垂直的性质可得 BC 平面 PAB ,再由线面垂直的性质可得 BC PB 即 BC EF ,再结合 BC DE ,由线面垂直的判定即可得证. 【详解】证明:(1)因为 / /AD BC , 2BC AD , E 为 BC 的中点. 所以 / /AD BE 且 AD BE ,所以四边形 ADEB 是平行四边形, 所以 / /AB DE , 又因为 AB 平面 DEF , DE 平面 DEF 所以 / /AB 平面 DEF ; (2)因为平面 PAB 平面 ABCD ,平面 PAB 平面 ABCD AB , AB BC , BC 平面 ABCD 所以 BC 平面 PAB , 因为 PB 平面 PAB .所以 BC PB , 因为 E , F 分别为 BC , PC 的中点, 所以 / /EF PB ,所以 BC EF , 因为 / /AB DE , BC AB ,所以 BC DE , 因为 DE 平面 DEF , EF 平面 DEF , DE EF E 所以 BC 平面 DEF . 【点睛】本题考查了线线、线面、面面关系的判定与性质,考查了空间思维能力,属于中档 题. 16.如图,在 ABC 中, 6AC ,D 为 AB 边上一点, 2CD AD ,且 6cos 4BCD . (1)求sinB ; (2)求 ABC 的面积. 【答案】(1) 10 8 ;(2) 3 15 2 . - 12 - 【解析】 【分析】 (1)由余弦定理结合题意可得 1cos 4ADC ,根据同角三角函数的平方关系可得 15sin 4ADC 、 10sin 4BCD ,再利用 sin sinB ADC BCD 即可得解; (2)由正弦定理可得 sin sin sin BD CD BC BCD B BDC ,进而可求得 4BD 、 2 6BC , 利用三角形面积公式即可得解. 【详解】(1)在 ADC 中,由余弦定理得 22 22 2 2 2 2 6 1cos 2 2 2 2 4 AD CD ACADC AD CD 所以 2 2 1 15sin 1 cos 1 4 4ADC ADC 因为 6cos 4BCD , BCD 是三角形 BCD 的内角, 所以 2 2 6 10sin 1 cos 1 4 4BCD BCD 所以 sin sinB ADC BCD sin cos cos sinADC BCD ADC BCD 15 6 1 10 4 4 4 4 10 8 ; (2)在 BCD 中,由正弦定理得 sin sin sin BD CD BC BCD B BDC , 所以 102sin 4 4sin 10 8 CD BCDBD B , 152sin sin 4 2 6sin sin 10 8 CD BDC CD ADCBC B B , 所以 6AB AD BD , - 13 - 所以 1 1 10 3 15sin 6 2 62 2 8 2ABCS AB BC B . 【点睛】本题考查了正弦定理、余弦定理及三角恒等变换的综合应用,考查了运算求解能力, 属于中档题. 17.某公司准备设计一个精美的心形巧克力盒子,它是由半圆 1O 、半圆 2O 和正方形 ABCD 组成 的,且 8AB cm .设计人员想在心形盒子表面上设计一个矩形的标签 EFGH,标签的其中两 个顶点 E,F 在 AM 上,另外两个顶点 G,H 在 CN 上(M,N 分别是 AB,CB 的中点).设 EF 的中 点为 P, 1FO P ,矩形 EFGH 的面积为 2Scm . (1)写出 S 关于 的函数关系式 ( )S (2)当 为何值时矩形 EFGH 的面积最大? 【答案】(1) ( ) 32sin (2cos 2)S , 0, 4 ;(2)当 为 4 时,矩形 EFGH 的 面积最大,为 264cm . 【解析】 【分析】 (1)由题意知 0, 4 ,可得 8sinEF , 8cos 4 2EH ,利用矩形的面积公式, 即可得答案; (2)利用导数可得:当 0, 4 时, ( ) 0S 恒成立,所以 ( )S 在 0, 4E 上单调递 增,即可得答案; - 14 - 【详解】(1)由题意知 0, 4 , 8sinEF , 8cos 4 2EH , 则 ( ) 8sin (8cos 4 2)S EF EH , 即 ( ) 32sin (2cos 2)S , 0, 4 (2) ( ) 32[cos (2cos 2) sin ( 2sin )]S 2 232 2cos 2sin 2 cos 232 4cos 2 cos 2 . 因为 0, 4 ,所以 22 4cos 4 ,1 2 cos 2 ,所以 24cos 2 cos 2 0 , 故当 0, 4 时, ( ) 0S 恒成立,所以 ( )S 在 0, 4E 上单调递增. 故当 4 时, max( ) 32sin 2cos 2 644 4S . 答:当 为 4 时,矩形 EFGH 的面积最大,为 264cm . 【点睛】本题考查导数在实际问题中的运用,考查函数与方程思想,考查逻辑推理能力、运 算求解能力. 18.在平面直角坐标系 xOy 中,椭圆 2 2 2 2: 1 0x yC a ba b 的上顶点到焦点的距离为 2, 离心率为 3 2 . (1)求椭圆C 的方程; (2)设 P 是椭圆C 长轴上的一个动点,过点 P 作斜率为 k 的直线l 交椭圆C 于 A , B 两点, 若 2 2PA PB 的值与点 P 的位置无关,求 k 的值. 【答案】(1) 2 2 14 x y ;(2) 1 2k . 【解析】 - 15 - 【分析】 (1)由题意结合椭圆性质可得 2a 、 3c ,由 2 2 2b a c 求出 2b 后即可得解; (2)设 ,0 2 2P m m , 1 1,A x y , 2 2,B x y ,直线l 的方程为 y k x m ,联 立方程可得 2 1 2 2 8 1 4 mkx x k , 2 2 1 2 2 4 1 1 4 k m x x k ,进而可得 2 4 2 2 2 2 2 22 8 6 2 1 4 8 8 1 4 m k k k k PA PB k ,令 4 28 6 2 0k k 即可得解. 【详解】(1)由题设可知 2a , 3 2 ce a , 所以 3c ,所以 2 2 2 1b a c , 所以椭圆C 的方程为 2 2 14 x y ; (2)设 ,0 2 2P m m , 1 1,A x y , 2 2,B x y ,直线l 的方程为 y k x m , 将直线与椭圆的方程联立即 2 2 14 y k x m x y , 消去 y 得 2 2 2 2 21 4 8 4 1 0k x mk x k m , , 所以 2 1 2 2 8 1 4 mkx x k , 2 2 1 2 2 4 1 1 4 k m x x k , 所以 2 2 2 2 2 2 2 22 2 1 2 1 1 2 2 1 2 1 14 4 x xPA PB x m y x m y x m x m 2 4 2 2 2 2 2 2 1 2 1 2 22 8 6 2 1 4 8 83 2 2 24 1 4 m k k k k x x m x x m k , 因为 2 2PA PB 的值与点 P 的位置无关,即上式取值与 m 无关, 故有 4 28 6 2 0k k ,解得 1 2k . 【点睛】本题考查了椭圆标准方程的确定及直线与椭圆的综合应用,考查了运算求解能力, 属于中档题. - 16 - 19.已知函数 ln 1 2 1 2 2 x af x x ax x . (1)当 0a 时,求函数 f x 在 1x 处的切线方程; (2)若函数 f x 在定义域上单调增,求 a 的取值范围; (3)若函数 f x 在定义域上不单调,试判定 f x 的零点个数,并给出证明过程. 【答案】(1) 2 2y x ;(2) 2a ;(3)函数 f x 必有三个不同零点,证明详见解析. 【解析】 【分析】 (1)求导后可得 1 2f 即为切线斜率,再求出 1 0f ,利用点斜式即可得解; (2)转化条件得 2 2ln 2 3 0x x a 在 0x 时恒成立,令 2 2ln 2 3 0g x x x a x , 对 g x 求导后求出 ming x ,令 min 0g x 即可得解; (3)由题意若函数 f x 在定义域上不是单调函数 2a ,设 22ln 2 2 1h x x x ax a ,求导后,即可确定函数 h x 的零点个数,结合 1 0f 即可 得解. 【详解】(1)当 0a 时, ln 1 1 2 2 xf x xx x , 则 2 2 2 2 1 ln 1 1 2ln 3 2 2 2 x x xf x x x x , 1 0f , 则在 1x 处的切线斜率为 1 2f , 所以函数 f x 在 1x 处的切线方程为 2 1y x 即 2 2y x ; (2)因为 ln 2 1 2 2 x x af x a a Rx x . 所以 f x 的定义域为 0, , 2 2 2ln 2 3 2 x x af x x , 又因为函数 f x 在定义域上为单递增函数, 所以 2 2 2ln 2 3 02 x x af x x 在 0x 时恒成立, 即 2 2ln 2 3 0x x a 在 0x 时恒成立, - 17 - 设 2 2ln 2 3 0g x x x a x , 则 2 2 1 12 2 x xxg x x x , 当 0 1x 时, ( ) 0g x ,则 g x 在 0,1 上为减函数, 当 1x 时, 0g x ,则 g x 在 1, 上为增函数, 所以 2 2ln 2 3 0x x a 在 0x 时恒成立 min (1) 4 2 0g x g a , 所以 2a ; (3)因为 2 2 2ln 2 3 2 x x af x x , 所以 2 2 3 02 a a a ef e e ,则 0f x 不可能对 0x 恒成立, 即 f x 在定义域上不可能始终都为减函数, 由(2)知函数 f x 为增函数 2a , 所以若函数 f x 在定义域上不是单调函数 2a , 又因为 1 0f ,所以 1x 是函数 0f x 一个零点, 令 0f x 即 22ln 2 2 1 0x x ax a , 设 22ln 2 2 1h x x x ax a ,则 f x 与 h x 有相同的零点, 令 22( 1) 0x axh x x ,得 2 1 0x ax , 因为 2a ,所以 2 4 0a , 所以 2 1 0x ax 有两个不相等实数解 1x , 2x , 因为 1 2 1x x , 1 2 2x x a ,所以不妨设 1 20 1x x , 当 10,x x 时, 0h x , h x 在 10, x 为增函数; 当 1 2,x x x 时, 0h x , h x 在 10, x 为减函数; 当 1,x x 时, 0h x , h x 在 10, x 为增函数; 则 1 1 0h x h , 2 1 0h x h , - 18 - 又因为 2a 时, 0 1ae , 2 4a , 所以 2 21 2 0a a ah e e ae , 23 132 2ln 2 4 04 4h a a a , 又因为 f x 在 0,1 图象不间断,所以 f x 在 0,1 上有唯一零点; 又因为 f x 在 (1, ) 图象不间断,所以 f x 在 (1, ) 上有唯一零点; 又因为 1x 是函数 0f x 一个零点, 综上,函数 f x 必有三个不同零点. 【点睛】本题考查了导数的综合应用,考查了运算能力与推理能力,属于难题. 20.已知数列 na 的前 n 项和为 nS ,把满足条件 1n na S Nn 的所有数列 na 构成的集 合记为 M . (1)若数列 na 的通项为 1 2n na ,则 na 是否属于 M ? (2)若数列 na 是等差数列,且 na Mn ,求 1a 的取值范围; (3)若数列 na 的各项均为正数,且 na M ,数列 4n na 中是否存在无穷多项依次成等 差数列,若存在,给出一个数列 na 的通项;若不存在,说明理由. 【答案】(1) na M ;(2) 1 1a ;(3)数列 4n na 中是不存在无穷多项依次成等差数列, 理由详见解析. 【解析】 【分析】 (1)由题意可得 11 2 n nS ,证明 1 0n na S 即 1n na S 后即可得解; (2)由题意可得 2 1 1 1 3 1 1 02 2 2 d n a d n a ,当 1n 时, 1d ;结合二次函 数的性质可得 1 02 d ;即可得 1d ;进而可得 1 1 1 0a n ,即可得解; - 19 - (3)转化条件得 2 * 1 )2 (n na a n N 即 1 4 4 2 n n na a ,假设数列 4n na 中存在无穷多项依次 成等差数列,不妨设该等差数列的第 n 项为 dn b (b 为常数),则存在 m N , m n ,使 得 1 1 4 4 42 2 m m n m dn b a a a ,设 2 22n nf n , *n N , 3n ,作差后可得 91 3 132f n f n f 即当 3n 时, 2 22n n ,进而可得不等式 2 1 1 0n da n ba 有无穷多个解,显然不成立,即可得解. 【详解】(1)因为 1 2n na ,所以 111 12 112 21 2 n n nS , 所以 1 1 1 1 3 1 3 1 11 1 1 02 2 2 2 2 2 4 n n n n na S , 所以 1n na S ,即 na M ; (2)设 na 的公差为 d ,因为 na Mn , 所以 1 21 1 21n na n a a a n (*) 特别的当 1n 时, 2 12 1a a ,即 1d , 由(*)得 1 1 1 11 2 2 n n n na nd n na d , 整理得 2 1 1 1 3 1 1 02 2 2 d n a d n a , 因为上述不等式对一切 *n N 恒成立,所以必有 1 02 d ,解得 1d , 又 1d ,所以 1d , 于是 1 11 1 0a n a ,即 1 1 1 0a n , 所以 1 1 0a 即 1 1a ; (3)由 1n na S 得 1n n nS S S ,所以 1 2n nS S ,即 1 2n n S S , - 20 - 所以 1 3 12 1 1 2 2nn n n S S SS S S S S ,从而有 1 1 12 2n n nS S a , 又 1n na S ,所以 2 1 1 2n n na S a ,即 2 1 2 3n na a n - , 又 2 2 2 1 1 2a S a , 1 2 1 1 2a a ,所以有 2 * 1 )2 (n na a n N , 所以 1 4 4 2 n n na a , 假设数列 4n na 中存在无穷多项依次成等差数列, 不妨设该等差数列的第 n 项为 dn b (b 为常数), 则存在 m N , m n ,使得 1 1 4 4 42 2 m m n m dn b a a a ,即 2 1 1 2nda n ba , 设 2 22n nf n , *n N , 3n , 则 2 22 3 2 3 1 2 11 02 2 2n n n n nnf n f n , 即 91 3 132f n f n f , 于是当 3n 时, 2 22n n , 从而有:当 3n 时 2 1 1da n ba n ,即 2 1 1 0n da n ba , 于是当 3n 时,关于 n 的不等式 2 1 1 0n da n ba 有无穷多个解,显然不成立, 因此数列 4n na 中是不存在无穷多项依次成等差数列. 【点睛】本题考查了新概念在数列中的应用,考查了数列与函数的综合应用及反证法的应用, 属于难题. 第Ⅱ卷(附加题,共 40 分) 三、选做题 21.已知矩阵 3 0 0 4A . - 21 - (1)求 A 的逆矩阵 1A ; (2)求圆 2 2 144x y = 经过 1A 变换后所得的曲线的方程. 【答案】(1) -1 1 03 10 4 A ;(2) 2 2 116 9 x y . 【解析】 【分析】 (1)由题意结合 1 1 0 0 1AA ,即可得解; (2)求出圆上的点 ,P x y 经过 1A 变换后所得的点 ,P x y ,即可得解. 【详解】(1)由条件 3 0 0 4A 且 1 1 0 0 1AA ,可得 -1 1 03 10 4 A ; (2)设变换后新曲线上任一点 ,P x y ,变换前对应点 ,P x y , 则 1 03 10 4 x x y y ,即 1 3 1 4 x x y y , 所以 3 4 x x y y ,代入 2 2 144x y 得: 2 2 116 9 x y , 所以曲线 2 2 144x y 经过 1A 变换后所得曲线的方程为 2 2 116 9 x y . 【点睛】本题考查了逆矩阵的求解及矩阵变换的应用,考查了运算求解能力,属于基础题. 22.已知圆的参数方程为 1 2cos 3 2sin x y ( 为参数),以平面直角坐标系原点 O 为极点,x 轴的正半轴为极轴,取与直角坐标系相同的单位建立极坐标系,求过圆心且与极轴垂直的直 线的极坐标方程. 【答案】 cos 1 【解析】 【分析】 - 22 - 由题意消去参数可得圆的普通方程为 2 21 3 4x y ,进而可得过圆心且与极轴垂直的 直线的直角坐标方程为 1x ,由极坐标方程与直角坐标方程的转换公式即可得解. 【详解】由 1 2cos 3 2sin x y ( 为参数)消去参数得圆的普通方程为 2 21 3 4x y , 圆心坐标为 1,3 ,过圆心且与极轴垂直的直线的直角坐标方程为 1x , 则其极坐标方程为 cos 1 . 【点睛】本题考查了参数方程、直角坐标方程与极坐标方程的转化,属于基础题. 23.已知函数 1 2f x x x ,若 2 3 2a b c , ,a b c R ,且不等式 2 2 2a b c f x 恒成立,求实数 x 的取值范围. 【答案】 1,2 . 【解析】 【分析】 由柯西不等式得 2 2 2 2 2 36 a b ca b c ,转化条件得 3f x ,结合绝对值三角不 等式 1 2 1 2 3f x x x x x ,即可得解. 【详解】由柯西不等式可得 2 2 2 2 2 2 22 1 2 1a b c a b c , 所以 2 2 2 2 2 36 a b ca b c , 当且仅当 1 2 1 a b c 即 2b 、 2 2a c 时,等号成立, 所以 2 2 2a b c f x 恒成立 3f x , 因为 1 2 1 2 3f x x x x x ,当且仅当 1 2x 时,等号成立, 所以 3f x 的解集为 1 2x , 所以实数 x 的取值范围 1,2 . 【点睛】本题考查了柯西不等式与绝对值三角不等式的综合应用,考查了计算能力与转化化 归思想,属于中档题. - 23 - 四、必做题 24.如图,正四棱柱 1 1 1 1ABCD A B C D 中,设 1AD , 1 3DD ,点 P 在 1CC 上,且 1 2C P PC . (1)求直线 1A P 与平面 PDB 所成角的正弦值; (2)求二面角 A BD P 的余弦值. 【答案】(1) 2 2 3 ;(2) 3 3 . 【解析】 【分析】 (1)建立空间直角坐标系,求出各点坐标后,进而可得平面 PDB 一个法向量 1n ur 、直线 1A P 的方向向量 1A P ,利用 1 1sin cos ,A P n 即可得解; (2)取平面 ABD 一个法向量 2 0,0,1n uur ,利用 1 2 1 2 1 2 cos , n nn n n n 即可得解. 【详解】如图,以点 D 为原点O , DA , DC , 1DD 分别为 x , y , z 轴建立空间直角坐标 系O xyz , 则 0,0,0D , 1,1,0B , 1 1,0,3A , 0,11P ; - 24 - (1)所以 1 1,1, 2A P , 1,1,0DB , 0,1,1DP , 设平面 PDB 一个法向量为 1 , ,n x y z , 由 1 1 0 0 n DP n DB 得 0 0 y z x y ,令 1x ,则 1 1, 1,1n , 设直线 1A P 与平面 PDB 所成角为 , 所以 1 11 1 1 1 4 2 2sin cos , 36 3 A PA P n A P n n 所以直线 1A P 与平面 PDB 所成角的正弦值为 2 2 3 ; (2)由(1)知平面 PDB 一个法向量为 1 1, 1,1 n , 取平面 ABD 一个法向量 2 0,0,1n uur , 则 1 2 1 2 1 2 1 3cos , 33 n nn n n n , 由图知二面角 A BD P 为钝二面角, 所以二面角 A BD P 的余弦值为 3 3 . 【点睛】本题考查了利用空间向量求解线面角和二面角,考查了运算能力,属于中档题. - 25 - 25.已知抛物线C : 2 2y x 的焦点为 F ,平行于 x 轴的两条直线 1 2,l l 分别交C 于 A B, 两点, 交C 的准线于 P Q, 两点. (Ⅰ)若 F 在线段 AB 上, R 是 PQ 的中点,证明 / /AR FQ ; (Ⅱ)若 PQF 的面积是 ABF 的面积的两倍,求 AB 中点的轨迹方程. 【答案】(Ⅰ)见解析;(Ⅱ) 2 1y x . 【解析】 【分析】 设 2 2 1 1 1,0 , , , , , , , ,2 2 2 2 2 2 a b a bA B b P a Q b R l 的方程为 2 (x a ) 0b y ab .(Ⅰ)由 F 在线段 AB 上 1 0ab ,又 1 22 2 1 1 a b a b abk b ka a ab a a / /AR FQ ;(Ⅱ)设 l 与 x 轴的交点为 1,0D x 1 1 1 1 ,2 2 2 2ABF PQF a bS b a FD b a x S 1 1 1 2 2 2 a bb a x 1 0x (舍去), 1 1x .设满足条件的 AB 的中点为 ,E x y .当 AB 与 x 轴不垂直时 2 11 y xa b x 2 a b y 2 1 1y x x .当 AB 与 x 轴垂直时 E 与 D 重合 所求轨迹方程为 2 1y x . 【详解】由题设 1 ,02F ,设 1 2: , :l y a l y b ,则 0ab ,且 2 2 1 1 1,0 , , , , , , , ,2 2 2 2 2 2 a b a bA B b P a Q b R . 记过 ,A B 两点的直线为 l ,则l 的方程为 2 0x a b y ab (Ⅰ)由于 F 在线段 AB 上,故1 0ab , 记 AR 的斜率为 1,k FQ 的斜率为 2k ,则 1 22 2 1 1 a b a b abk b ka a ab a a , 所以 / /AR FQ - 26 - (Ⅱ)设 l 与 x 轴的交点为 1,0D x , 则 1 1 1 1 ,2 2 2 2ABF PQF a bS b a FD b a x S , 由题设可得 1 1 1 2 2 2 a bb a x ,所以 1 0x (舍去), 1 1x . 设满足条件的 AB 的中点为 ,E x y . 当 AB 与 x 轴不垂直时,由 AB DEk k 可得 2 11 y xa b x . 而 2 a b y ,所以 2 1 1y x x . 当 AB 与 x 轴垂直时, E 与 D 重合,所以,所求轨迹方程为 2 1y x 【点睛】本题考查了 1.抛物线定义与几何性质;2.直线与抛物线位置关系;3.轨迹求法. - 27 -查看更多