2020_2021学年新教材高中数学第7章三角函数7

2020_2021学年新教材高中数学第7章三角函数7

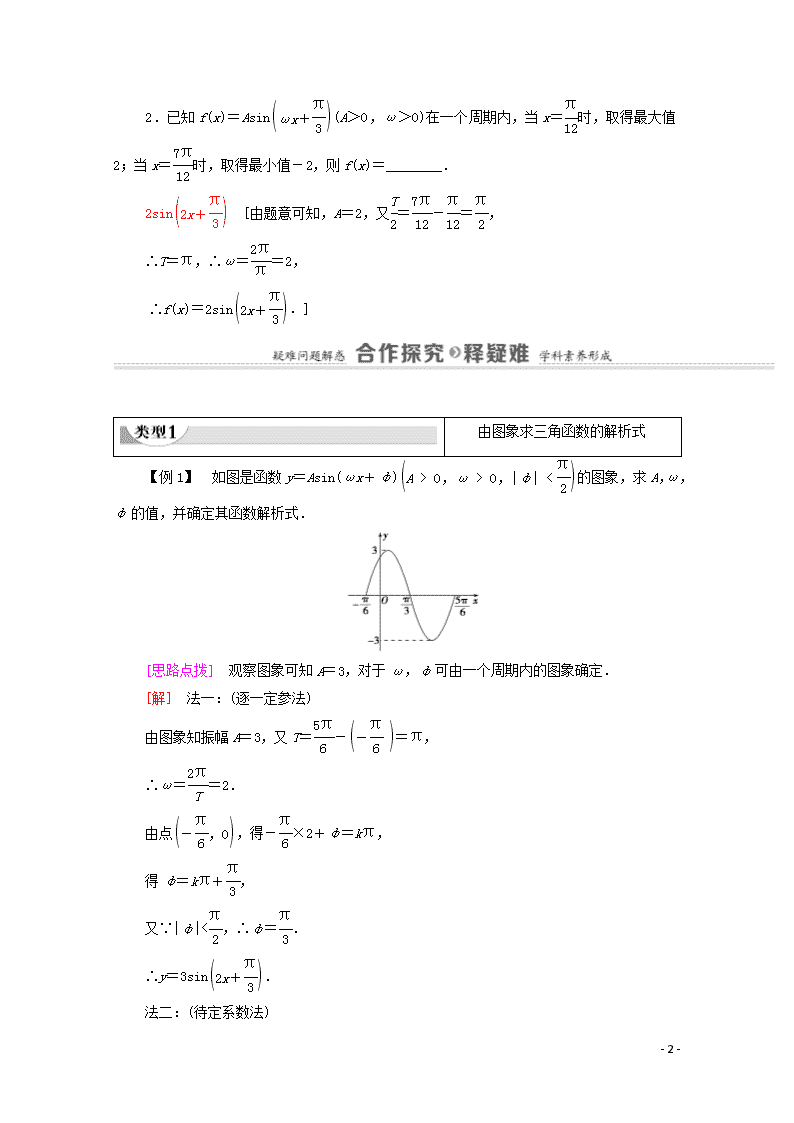
第2课时　函数y＝Asin(ωx＋φ)的图象与性质 学 习 目 标 核 心 素 养 ‎1．能由三角函数的图象求出解析式．(重点、易错点)‎ ‎2．掌握y＝Asin(ωx＋φ)的图象和性质．(重点)‎ 通过学习本节内容，提升学生的直观想象和数学运算的核心素养．‎ 用五点法作函数y＝Asin(ωx＋φ)在一个周期上的简图如何取点？函数y＝sin x与函数y＝Asin(ωx＋φ)存在着怎样的关系？从图象上看，函数y＝sin x与函数y＝Asin(ωx＋φ)存在着怎样的关系？φ，ω，A对y＝Asin(ωx＋φ)的图象又有什么影响？‎ 函数y＝Asin(ωx＋φ)(A＞0，ω＞0)的性质 定义域 R 值域 ‎[－A，A]‎ 周期性 T＝ 奇偶性 φ＝kπ，k∈Z时是奇函数；φ＝＋kπ，k∈Z时是偶函数；当φ≠(k∈Z)时是非奇非偶函数 单调性 单调增区间可由－＋2kπ≤ωx＋φ≤＋2kπ，k∈Z得到，单调减区间可由＋2kπ≤ωx＋φ≤＋2kπ，k∈Z得到 ‎1．最大值为，周期为，初相为的函数y＝Asin(ωx＋φ)(A＞0，ω＞0)解析式可以为________．‎ y＝sin　[由题意可知A＝，＝，∴ω＝6，又φ＝，故其解析式可以为y＝sin．]‎ ‎2．已知f(x)＝Asin(A＞0，ω＞0)在一个周期内，当x＝ - 9 -‎ 时，取得最大值2；当x＝时，取得最小值－2，则f(x)＝________．‎ ‎2sin　[由题意可知，A＝2，又＝－＝，‎ ‎∴T＝π，∴ω＝＝2，‎ ‎∴f(x)＝2sin．]‎ 由图象求三角函数的解析式 ‎【例1】　如图是函数y＝Asin(ωx＋φ)的图象，求A，ω，φ的值，并确定其函数解析式．‎ ‎[思路点拨]　观察图象可知A＝3，对于ω，φ可由一个周期内的图象确定．‎ ‎[解]　法一：(逐一定参法)‎ 由图象知振幅A＝3，又T＝－＝π，‎ ‎∴ω＝＝2．‎ 由点，得－×2＋φ＝kπ，‎ 得φ＝kπ＋，‎ 又∵|φ|<，∴φ＝．‎ ‎∴y＝3sin．‎ 法二：(待定系数法)‎ 由图象知A＝3，又图象过点和，根据五点作图法原理(以上两点可判为“五点法”中的第三点和第五点)，有解得 - 9 -‎ ‎∴y＝3sin．‎ 若设所求解析式为y＝Asin(ωx＋φ)，则在观察函数图象的基础上，可按以下规律来确定A，ω，φ.‎ (1)由函数图象上的最大值、最小值来确定|A|.‎ (2)由函数图象与x轴的交点与其对称轴确定T，由T＝，确定ω.‎ (3)确定函数y＝Asin(ωx＋φ)的初相φ的值的三种方法 ‎①代入法：把图象上的一个已知点代入(此时A，ω已知)或代入图象与x轴的交点求解(此时要注意交点在上升区间上还是在下降区间上).‎ ‎②五点对应法：确定φ值时，往往以寻找“五点法”中的第一个零点作为突破口.“五点”的ωx＋φ的值具体如下：‎ ‎“第一点”(即图象上升时与x轴的交点)为ωx＋φ＝0；‎ ‎“第二点”(即图象的“峰点”)为ωx＋φ＝；,‎ ‎“第三点”(即图象下降时与x轴的交点)为ωx＋φ＝π；‎ ‎“第四点”(即图象的“谷点”)为ωx＋φ＝；‎ ‎“第五点”为ωx＋φ＝2π.‎ ‎③图象变换法：运用逆向思维的方法，先确定函数的基本解析式y＝Asin ωx，再根据图象平移规律确定相关的参数.‎ ‎1．已知函数y＝Asin(ωx＋φ)(A>0，ω>0)在一个周期内的函数图象，如图所示，求该函数的一个解析式．‎ ‎[解]　法一：(最值点法)由图象知函数的最大值为，最小值为－，又A>0，∴A＝．‎ - 9 -‎ 由图象知＝－＝，∴T＝π＝，∴ω＝2．‎ 又＝，∴图象上的最高点为，‎ ‎∴＝sin，即sin＝1，则＋φ＝＋2kπ，φ＝－＋2kπ，可取φ＝－，‎ ‎∴函数的一个解析式为y＝sin．‎ 法二：(五点对接法)由图象知A＝，又图象过点，，根据五点作图法原理(以上两点可判断为五点作图法中的第一点与第三点)得解得∴函数的一个解析式为y＝sin．‎ 法三：(图象变换法)由图可知A＝，＝－＝，‎ ‎∴T＝π＝，∴ω＝2．‎ ‎∴该函数的图象可由y＝sin 2x的图象向右平移个单位长度得到，‎ ‎∴所求函数的一个解析式为y＝sin 2，‎ 即y＝sin．‎ y＝Asin(ωx＋φ)(A＞0，ω＞0)的性质 ‎[探究问题]‎ ‎1．函数y＝Asin(ωx＋φ)(A＞0，ω＞0)的奇偶性与哪个量有关？当其取何值时为偶函数？当其取何值时为奇函数？‎ ‎[提示]　函数y＝Asin(ωx＋φ)(A＞0，ω＞0)的奇偶性与参数φ有关，当φ＝＋kπ，k∈Z时，其为偶函数，当φ＝kπ，k∈Z时，其为奇函数．‎ ‎2．函数y＝Asin(ωx＋φ)(A＞0，ω＞0)的对称轴方程如何表示，对称中心呢？‎ ‎[提示]　由ωx＋φ＝＋kπ，k∈Z，求对称轴方程；由ωx＋φ＝kπ，k∈Z，求对称中心．‎ ‎3．函数y＝Asin(ωx＋φ)(A＞0，ω - 9 -‎ ‎＞0)中，相邻对称轴之间相差多少个周期？相邻根之间呢？‎ ‎[提示]　均相差半个周期．‎ ‎【例2】　已知函数y＝Asin(ωx＋φ)的图象过点P，图象上与P点最近的一个最高点的坐标为，求函数的解析式．‎ ‎[思路点拨]　由图象过P和离P最近的最高点可求A，ω，由是最高点及|φ|<可求得φ的值．‎ ‎[解]　∵图象最高点的坐标为，‎ ‎∴A＝5．‎ ‎∵＝－＝，∴T＝π，‎ ‎∴ω＝＝2，∴y＝5sin(2x＋φ)．‎ 代入点，得sin＝1，‎ ‎∴＋φ＝2kπ＋，k∈Z．‎ ‎∴φ＝－＋2kπ，k∈Z．‎ 又∵|φ|<，∴k＝0，则φ＝－，‎ ‎∴y＝5sin．‎ ‎1．(变结论)本例条件不变，指出函数的单调增区间．‎ ‎[解]　∵函数的单调增区间满足2kπ－≤2x－≤2kπ＋(k∈Z)，‎ ‎∴2kπ－≤2x≤2kπ＋(k∈Z)，‎ ‎∴kπ－≤x≤kπ＋(k∈Z)．‎ ‎∴函数的单调增区间为(k∈Z)．‎ ‎2．(变结论)本例条件不变，求使y≤0的x的取值范围．‎ ‎[解]　∵5sin≤0，‎ - 9 -‎ ‎∴2kπ－π≤2x－≤2kπ(k∈Z)，‎ ‎∴kπ－≤x≤kπ＋(k∈Z)．‎ 故所求x的取值范围是(k∈Z)．‎ 有关函数y＝Asin(ωx＋φ)的性质的问题，要充分利用正弦曲线的性质，要特别注意整体代换思想.‎ 提醒：熟知y＝Asin(ωx＋φ)的图象和性质是解决y＝Asin(ωx＋φ)类综合题的关键.‎ ‎2．已知函数f(x)＝sin(ω＞0)的最小正周期为π，则该函数图象(　　)‎ A．关于点对称 B．关于直线x＝对称 C．关于点对称 D．关于直线x＝对称 A　[由T＝＝π，解得ω＝2，则f(x)＝sin，‎ 则该函数图象关于点对称．]‎ ‎3．(多选题)函数f(x)＝3sin的图象为C，则以下结论中正确的是(　　)‎ A．图象C关于直线x＝对称 B．图象C关于点对称 C．函数f(x)在区间内是增函数 D．由y＝3sin 2x的图象向右平移个单位长度可以得到图象C BC　[f＝3sin＝3sin＝－，f＝3sin - 9 -‎ ‎＝0，故A错，B正确；令－＋2kπ≤2x－≤＋2kπ，k∈Z，解得－＋kπ≤x≤＋kπ，k∈Z，故C正确；函数y＝3sin 2x的图象向右平移个单位长度，得到函数y＝3sin 2＝3sin的图象，故D错．故选BC．]‎ ‎1．由函数y＝Asin(ωx＋φ)的部分图象确定解析式关键在于确定参数A，ω，φ的值．‎ ‎(1)一般可由图象上的最大值、最小值来确定|A|．‎ ‎(2)因为T＝，所以往往通过求周期T来确定ω，可通过已知曲线与x轴的交点从而确定T，即相邻的最高点与最低点之间的水平距离为；相邻的两个最高点(或最低点)之间的水平距离为T．‎ ‎(3)从寻找“五点法”中的第一个零点(也叫初始点)作为突破口，以y＝Asin(ωx＋φ)(A＞0，ω＞0)为例，位于单调递增区间上离y轴最近的那个零点最适合作为“五点”中的第一个点．‎ ‎2．在研究y＝Asin(ωx＋φ)(A＞0，ω＞0)的性质时，注意采用整体代换的思想．例如，它在ωx＋φ＝＋2kπ(k∈Z)时取得最大值，在ωx＋φ＝＋2kπ(k∈Z)时取得最小值．‎ ‎1．(多选题)关于x的函数f(x)＝sin(x＋φ)的以下说法，正确的是(　　)‎ A．对任意的φ，f(x)都是非奇非偶函数 B．存在φ，使f(x)是偶函数 C．存在φ，使f(x)是奇函数 D．对任意的φ，f(x)都不是偶函数 BC　[当φ＝0时，f(x)＝sin x，是奇函数；当φ＝时，f(x)＝cos x，是偶函数．故选BC．]‎ ‎2．(一题两空)如图是函数y＝sin(ωx＋φ)的图象的一部分，那么ω＝________，φ＝________．‎ - 9 -‎ 　　[∵点在函数图象上，∴sin φ＝．‎ 又∵|φ|<，∴φ＝，∴y＝sin．‎ 又∵点(π，0)在y＝sin上，且该点是“五点”中的第五个点，‎ ‎∴sin＝0，∴πω＋＝2π，∴ω＝．]‎ ‎3．函数y＝sin的图象的一条对称轴方程是________．‎ x＝(答案不唯一)　[由2x＋＝kπ＋(k∈Z)，得x＝＋(k∈Z)，令k＝0，得x＝．]‎ ‎4．已知曲线y＝Asin(ωx＋φ)(A＞0，ω＞0)上的一个最高点的坐标为，此点到相邻最低点间的曲线与x轴交于点，若φ∈．‎ ‎(1)试求这条曲线的函数表达式；‎ ‎(2)用“五点法”画出(1)中函数在[0，π]上的图象．‎ ‎[解]　(1)由题意知A＝ ，‎ T＝4×＝π，‎ ω＝＝2，∴y＝sin(2x＋φ)．‎ 又∵sin＝1，‎ ‎∴＋φ＝2kπ＋，k∈Z，‎ ‎∴φ＝2kπ＋，k∈Z，‎ 又∵φ∈，‎ ‎∴φ＝，‎ - 9 -‎ ‎∴y＝sin．‎ ‎(2)列出x，y的对应值表：‎ x ‎－ π π π ‎2x＋ ‎0‎ π π ‎2π y ‎0‎ ‎0‎ ‎－ ‎0‎ 描点、连线，如图所示：‎ - 9 -‎