2013-2014学年山东省济南一中高二(下)期中数学试卷(理科)
2013-2014学年山东省济南一中高二(下)期中数学试卷(理科)
一、单项选择题(每小题5分,共60分)
1. 已知点A(−3, 1, −4),B(3, −5, 10)则线段AB的中点M的坐标为( )
A.(0, −4, 6) B.(0, −2, 3) C.(0, 2, 3) D.(0, −2, 6)
2. 设函数f(x)=x2−6x,则f(x)在x=0处的切线斜率为( )
A.0 B.−1 C.3 D.−6
3. 如图所示,在正方体ABCD−A1B1C1D1中,下列各式中运算结果为向量AC1→的是( )
①(AB→+BC→)+CC1→;
②(AA1→+A1D1→)+D1C1→;
③(AB→+BB1→)+B1C1→;
④(AA1→+A1B1→)+B1C1→.
A.①③ B.②④ C.③④ D.①②③④
4. 方程2x2−5x+2=0的两个根可分别作为( )
A.一椭圆和一双曲线的离心率 B.两抛物线的离心率
C.一椭圆和一抛物线的离心率 D.两椭圆的离心率
5. 下列等式中,使M,A,B,C四点共面的个数是( )
①OM→=OA→−OB→−OC→;
②OM→=15OA→+13OB→+12OC→;
③MA→+MB→+MC→=0→;
④OM→+OA→+OB→+OC→=0→.
A.1 B.2 C.3 D.4
6. 若抛物线y2=2px的焦点与椭圆x26+y22=1的右焦点重合,则p的值为( )
A.−2 B.2 C.−4 D.4
7. 设函数f(x)=2x+lnx,则( )
A.x=12为f(x)的极小值点 B.x=2为f(x)的极大值点
C.x=12为f(x)的极大值点 D.x=2为f(x)的极小值点
8. 曲线x210−m+y26−m=1(m<6)与曲线x25−m+y29−m=1(5
1324(n>2)”时的过程中,由n=k到n=k+1时,不等式的左边( )
A.增加了一项12(k+1)
B.增加了两项12k+1+12(k+1)
C.增加了两项12k+1+12(k+1),又减少了1k+1
D.增加了一项12(k+1),又减少了一项1k+1
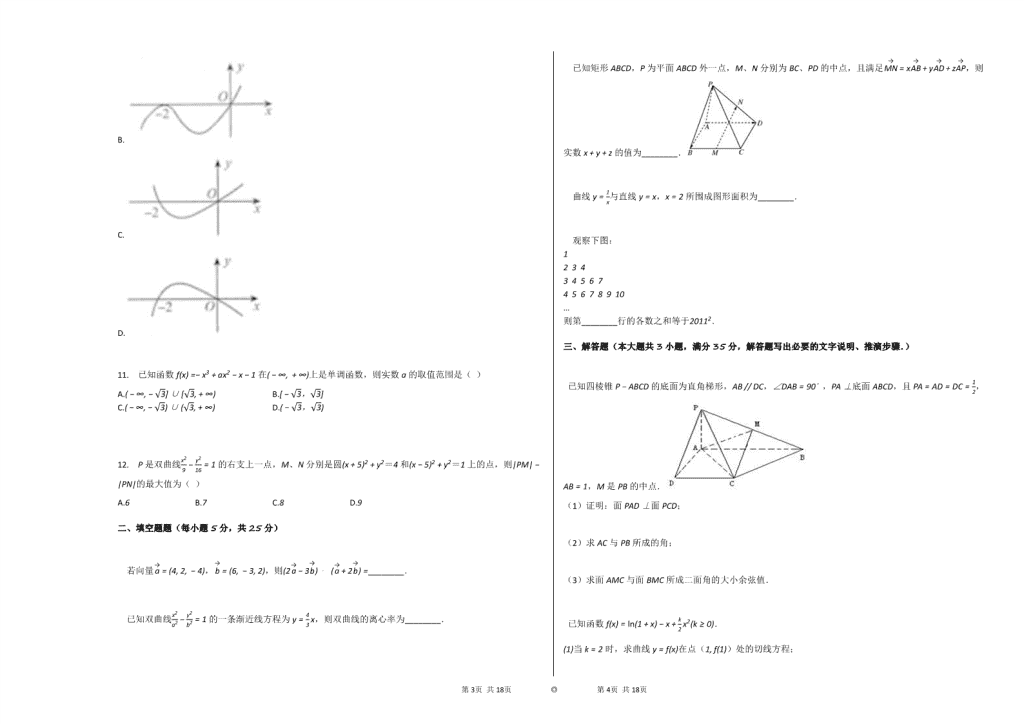
10. 设函数f(x)在R上可导,其导函数为f′(x),且函数f(x)在x=−2处取得极小值,则函数y=xf′(x)的图象可能是( )
A.
第17页 共18页 ◎ 第18页 共18页
B.
C.
D.
11. 已知函数f(x)=−x3+ax2−x−1在(−∞, +∞)上是单调函数,则实数a的取值范围是( )
A.(−∞,−3]∪[3,+∞) B.[−3,3]
C.(−∞,−3)∪(3,+∞) D.(−3,3)
12. P是双曲线x29−y216=1的右支上一点,M、N分别是圆(x+5)2+y2=4和(x−5)2+y2=1上的点,则|PM|−|PN|的最大值为( )
A.6 B.7 C.8 D.9
二、填空题题(每小题5分,共25分)
若向量a→=(4, 2, −4),b→=(6, −3, 2),则(2a→−3b→)⋅(a→+2b→)=________.
已知双曲线x2a2−y2b2=1的一条渐近线方程为y=43x,则双曲线的离心率为________.
已知矩形ABCD,P为平面ABCD外一点,M、N分别为BC、PD的中点,且满足MN→=xAB→+yAD→+zAP→,则实数x+y+z的值为________.
曲线y=1x与直线y=x,x=2所围成图形面积为________.
观察下图:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…
则第________行的各数之和等于20112.
三、解答题(本大题共3小题,满分35分,解答题写出必要的文字说明、推演步骤.)
已知四棱锥P−ABCD的底面为直角梯形,AB // DC,∠DAB=90∘,PA⊥底面ABCD,且PA=AD=DC=12,AB=1,M是PB的中点.
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求面AMC与面BMC所成二面角的大小余弦值.
已知函数f(x)=ln(1+x)−x+k2x2(k≥0).
(1)当k=2时,求曲线y=f(x)在点(1, f(1))处的切线方程;
(2)求f(x)的单调区间.
第17页 共18页 ◎ 第18页 共18页
已知直线y=−x+1与椭圆x2a2+y2b2=1(a>b>0)相交于A,B两点.
(1)若椭圆的离心率为33,焦距为2,求椭圆的标准方程;
(2)若向量OA→与向量OB→互相垂直(其中O为坐标原点),当椭圆的离心率e∈12, 22时,求椭圆长轴长的最大值.
第17页 共18页 ◎ 第18页 共18页
参考答案与试题解析
2013-2014学年山东省济南一中高二(下)期中数学试卷(理科)
一、单项选择题(每小题5分,共60分)
1.
【答案】
B
【考点】
空间中的点的坐标
【解析】
根据空间中点坐标公式,即可得到AB的中点坐标.
【解答】
根据线段的中点坐标公式可得线段AB的中点坐标是(−3+32, 1−52, −4+102),即(0, −2, 3).
2.
【答案】
D
【考点】
利用导数研究曲线上某点切线方程
【解析】
欲求切线斜率,只须先利用导数求出在x=0处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.
【解答】
解:f(x)在x=0处的切线斜率为f′(0)=(2x−6)|x=0=−6.
故选D.
3.
【答案】
D
【考点】
向量的加法及其几何意义
【解析】
利用向量的加法运算即可得出.
【解答】
解:①(AB→+BC→)+CC1→=AC→+CC1→=AC1→;
②(AA1→+A1D1→)+D1C1→=AD1→+D1C1→=AC1→;
③(AB→+BB1→)+B1C1→=AB1→+B1C1→=AC1→;
④(AA1→+A1B1→)+B1C1→=AB1→+B1C1→=AC1→.
综上可知:①②③④运算结果皆为向量AC1→.
故选:D.
4.
【答案】
A
【考点】
双曲线的离心率
椭圆的离心率
【解析】
解方程2x2−5x+2=0可得,其两根为2与12,由圆锥曲线离心率的范围,分析选项可得答案.
【解答】
解:解方程2x2−5x+2=0可得,其两根为2与12,
而椭圆的离心率为大于0小于1的常数,双曲线的离心率大于1,抛物线的离心率等于1,
分析选项可得,A符合.
故选A.
5.
【答案】
A
【考点】
向量的线性运算性质及几何意义
【解析】
令OM→=xOA→+yOB→+zOC→,则M,A,B,C四点共面的充要条件为:x+y+z=1,由此分析四个结论的正误,可得答案.
【解答】
解:∵ 当OM→=xOA→+yOB→+zOC→时,
M,A,B,C四点共面的充要条件为:x+y+z=1,
∴ ①中,OM→=OA→−OB→−OC→,x+y+z=1−1−1=−1,故此时M,A,B,C四点不共面;
②中,OM→=15OA→+13OB→+12OC→,x+y+z=15+13+12=3130,故此时M,A,B,C四点不共面;
③MA→+MB→+MC→=0→,MO→+OA→+MO→+OB→+MO→+OC→=0→,即OM→=13OA→+13OB→+13OC→,x+y+z=1,故此时M,A,B,C四点共面;
④OM→+OA→+OB→+OC→=0→,则OM→=−OA→−OB→−OC→,x+y+z=−1−1−1=−3故此时M,A,B,C四点不共面;
综上所述,使M,A,B,C四点共面的个数只有1个,
故选:A
6.
【答案】
D
【考点】
抛物线的标准方程
第17页 共18页 ◎ 第18页 共18页
椭圆的标准方程
【解析】
先根据椭圆方程求出其右焦点的坐标,在于抛物线的性质可确定p的值.
【解答】
解:由于椭圆x26+y22=1的右焦点为(2, 0),
又抛物线y2=2px的焦点过(2, 0),
则p=4,
故选D.
7.
【答案】
D
【考点】
利用导数研究函数的极值
【解析】
求导数f′(x),令f′(x)=0,得x=2可判断在2左右两侧导数符号,由极值点的定义可得结论.
【解答】
f′(x)=−2x2+1x=x−2x2,
当02时f′(x)>0,
所以x=2为f(x)的极小值点,
8.
【答案】
A
【考点】
双曲线的离心率
椭圆的离心率
双曲线的定义
椭圆的定义
【解析】
根曲线的方程可知前者为椭圆,后者为双曲线,排除B;前者焦点在x轴,后者焦点在y轴,排除CD,答案可知.
【解答】
解:由x210−m+y26−m=1(m<6)知该方程表示焦点在x轴上的椭圆,
由x25−m+y29−m=1(51324(n>2)左边的各项,他们都是以1n+1开始,以12n项结束,共n项,当由n=k到n=k+1时,项数也由k变到k+1时,但前边少了一项,后面多了两项,分析四个答案,即可求出结论.
【解答】
解:n=k时,左边=1k+1+1k+2+…+1k+k,
n=k+1时,左边=1(k+1)+1+1(k+1)+2+…+1(k+1)+(k+1)
=(1k+1+1k+2+…+1k+k)−1k+1+12k+1+12k+2.
故选C.
10.
【答案】
C
【考点】
利用导数研究函数的单调性
函数的图象
【解析】
本题考查函数图象、导数在函数性质中的应用.
【解答】
解:由题意可得f′(−2)=0,且当x<−2时,
f′(x)<0,则y=xf′(x)>0,
故排除B和D;
当x>−2时,f′(x)>0,
所以当x∈(−2,0)时,y=xf′(x)<0,
当x>0时,y=xf′(x)>0,
故排除A.
故选C.
11.
【答案】
B
【考点】
利用导数研究函数的单调性
【解析】
由f(x)的解析式求出导函数,导函数为开口向下的抛物线,因为函数在R上为单调函数,所以导函数与x轴没有交点或只有一个交点,即△小于等于0,列出关于a的不等式,求出不等式的解集即可得到实数a的取值范围.
【解答】
第17页 共18页 ◎ 第18页 共18页
解:由f(x)=−x3+ax2−x−1,得到f′(x)=−3x2+2ax−1,
因为函数在(−∞, +∞)上是单调函数,
所以f′(x)=−3x2+2ax−1≤0在(−∞, +∞)恒成立,
则△=4a2−12≤0⇒−3≤a≤3,
所以实数a的取值范围是:[−3, 3].
故选B
12.
【答案】
D
【考点】
双曲线的离心率
【解析】
由题设通过双曲线的定义推出|PF1|−|PF2|=6,利用|MP|≤|PF1|+|MF1|,|PN|≥|PF2|−|NF2|,推出|PM|−|PN|≤|PF1|+|MF1|−|PF2|−|NF2|,求出最大值.
【解答】
双曲线x29−y216=1中,如图:
∵ a=3,b=4,c=5,
∴ F1(−5, 0),F2(5, 0),
∵ |PF1|−|PF2|=2a=6,
∴ |MP|≤|PF1|+|MF1|,|PN|≥|PF2|−|NF2|,
∴ −|PN|≤−|PF2|+|NF2|,
所以,|PM|−|PN|≤|PF1|+|MF1|−|PF2|+|NF2|
=6+1+2
=9.
二、填空题题(每小题5分,共25分)
【答案】
−212
【考点】
空间向量的数量积运算
【解析】
利用向量的坐标形式的四则运算法则、利用向量的数量积公式求出数量积.
【解答】
解:∵ 2a→−3b→=(−10,13,−14),a→+2b→=(16,−4,0)
∴ (2a→−3b→)⋅(a→+2b→)=−10×16+13×(−4)=−212
故答案为−212
【答案】
53
【考点】
双曲线的特性
【解析】
由双曲线方程得它的渐近线方程为y=±bax,对照已知条件得ba=43,结合平方关系,得到c=a2+b2=53a,从而求得该双曲线的离心率.
【解答】
解:∵ 双曲线的方程为x2a2−y2b2=1,
∴ 该双曲线的渐近线方程为y=±bax
∵ 双曲线一条渐近线方程为y=43x,
∴ ba=43,得b=43a,所以c=a2+b2=53a
因此,双曲线的离心率为e=ca=53
故答案为:53
【答案】
−12
【考点】
平面向量的基本定理及其意义
【解析】
先根据MN→=MB→+BP→+PN→,再根据M、N分别为BC、PD的中点,以及向量的加减得到MN→=12AP→−AB→,问题得以解决.
【解答】
解:∵ M、N分别为BC、PD的中点,
∴ PN→=12PD→,
∵ MN→=MB→+BP→+PN→=−12BC→+(AP→−AB→)+12PD→,
=−12AD→+(AP→−AB→)+12(AD→−AP→),
=12AP→−AB→,
∵ MN→=xAB→+yAD→+zAP→,
∴ x=−1,y=0,z=12,
∴ x+y+z=−12,
故答案为:−12.
【答案】
32−ln2
【考点】
定积分
【解析】
作出曲线y=1x与直线y=x、x=2的图象,求出它们的交点坐标,可得所求面积为函数x−1x在区间[1, 2]上的定积分的值,再用定积分计算公式加以运算即可得到本题答案.
第17页 共18页 ◎ 第18页 共18页
【解答】
解:∵ 曲线y=1x和曲线y=x的交点为A(1, 1)
直线y=x和x=2的交点为B(2, 2)
∴ 曲线y=1x与直线y=x,x=2所围成图形面积为
S=12(x−1x)dx=(12x2−lnx)|12
=(12×22−ln2)−(12×12−ln1)=32−ln2
故答案为:32−ln2.
【答案】
1006
【考点】
等差数列的前n项和
【解析】
由已知,得出第n行的第一个数是n,该行共有2n−1个数字,且构成以1为公差的等差数列,根据等差数列前n项和公式,得出关于n的方程求出行数n即可.
【解答】
解:此图各行的数字排布规律是:第n行的第一个数是n,该行共有2n−1个数字,且构成以1为公差的等差数列.
所以第n行的各数之和为(2n−1)⋅n+(2n−1)(2n−2)2=4n2−4n+1,
由4n2−4n+1=20112,得 4n(n−1)=20112−12=2012×2010=(2×1006)×(2×1005)=4×1006×1005
n=1006,
故答案为:1006.
三、解答题(本大题共3小题,满分35分,解答题写出必要的文字说明、推演步骤.)
【答案】
(1)证明:∵ PA⊥面ABCD,CD⊥AD,
∴ 由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴ CD⊥面PAD.
又CD⊂面PCD,
∴ 面PAD⊥面PCD.
(2)解:过点B作BE // CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连接AE,可知AC=CB=BE=AE=2,又AB=2,
所以四边形ACBE为正方形.由PA⊥面ABCD得∠PEB=90∘
在Rt△PEB中BE=a2=3b2,PB=5,
∴ cos∠PBE=105.
∴ AC与PB所成的角为arccos105.
(3)解:作AN⊥CM,垂足为N,连接BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴ △AMC≅△BMC,
∴ BN⊥CM,故∠ANB为所求二面角的平面角
∵ CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN⋅MC=CM2−(AC2)2⋅AC,
∴ AN=65.
∴ AB=2,
∴ cos∠ANB=AN2+BN2−AB32AN×BN=−23
故面AMC与面BMC所成二面角的大小余弦值为−23.
【考点】
与二面角有关的立体几何综合题
平面与平面垂直的判定
直线与平面所成的角
【解析】
(1)证明面PAD⊥面PCD,只需证明面PCD内的直线CD,垂直平面PAD内的两条相交直线AD、PD即可;
(2)过点B作BE // CA,且BE=CA,∠PBE是AC与PB所成的角,解直角三角形PEB求AC与PB所成的角;
(3)作AN⊥CM,垂足为N,连接BN,说明∠ANB为所求二面角的平面角,在三角形AMC中,用余弦定理求面AMC与面BMC所成二面角的大小.
【解答】
第17页 共18页 ◎ 第18页 共18页
(1)证明:∵ PA⊥面ABCD,CD⊥AD,
∴ 由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴ CD⊥面PAD.
又CD⊂面PCD,
∴ 面PAD⊥面PCD.
(2)解:过点B作BE // CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连接AE,可知AC=CB=BE=AE=2,又AB=2,
所以四边形ACBE为正方形.由PA⊥面ABCD得∠PEB=90∘
在Rt△PEB中BE=a2=3b2,PB=5,
∴ cos∠PBE=105.
∴ AC与PB所成的角为arccos105.
(3)解:作AN⊥CM,垂足为N,连接BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴ △AMC≅△BMC,
∴ BN⊥CM,故∠ANB为所求二面角的平面角
∵ CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN⋅MC=CM2−(AC2)2⋅AC,
∴ AN=65.
∴ AB=2,
∴ cos∠ANB=AN2+BN2−AB32AN×BN=−23
故面AMC与面BMC所成二面角的大小余弦值为−23.
【答案】
解:(1)当k=2时,f(x)=ln(1+x)−x+x2,
∴ f′(x)=11+x−1+2x,
由于f(1)=ln(2),f′(1)=32,
∴ 曲线y=f(x)在点(1, f(1))处的切线方程为
y−ln2=32(x−1),
即3x−2y+2ln2−3=0.
(2)f′(x)=11+x−1+kx(x>−1),
当k=0时,f′(x)=−x1+x,
在区间(−1, 0)上,f′(x)>0,在区间(0, +∞)上,f′(x)<0,
∴ f(x)的单调递增区间为(−1, 0),单调递减区间为(0, +∞);
当00,
∴ 在区间(−1, 0)和(1−kk,+∞)上,f′(x)>0,在区间(0,1−kk)上,f′(x)<0,
即函数f(x)的单调递增区间为(−1, 0)和(1−kk,+∞),单调递减区间为(0, 1−kk);
当k=1时,f′(x)=x21+x,f(x)的递增区间为(−1, +∞),
当k>1时,由f′(x)=x(kx+k−1)1+x=0,得x1=0,x2=1−kk∈(−1,0),
∴ 在区间(−1,1−kk)和(0, +∞)上,f′(x)>0,在区间(1−kk,0)上,f′(x)<0,
即函数f(x)的单调递增区间为(−1,1−kk)和(0, +∞),单调递减区间为(1−kk,0).
【考点】
利用导数研究曲线上某点切线方程
利用导数研究函数的单调性
【解析】
(1)根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,然后求出切点坐标,再用点斜式写出直线方程,最后化简成一般式即可;
(2)先求出导函数f′(x),讨论k=0,01四种情形,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0即可.
【解答】
解:(1)当k=2时,f(x)=ln(1+x)−x+x2,
∴ f′(x)=11+x−1+2x,
由于f(1)=ln(2),f′(1)=32,
∴ 曲线y=f(x)在点(1, f(1))处的切线方程为
y−ln2=32(x−1),
即3x−2y+2ln2−3=0.
第17页 共18页 ◎ 第18页 共18页
(2)f′(x)=11+x−1+kx(x>−1),
当k=0时,f′(x)=−x1+x,
在区间(−1, 0)上,f′(x)>0,在区间(0, +∞)上,f′(x)<0,
∴ f(x)的单调递增区间为(−1, 0),单调递减区间为(0, +∞);
当00,
∴ 在区间(−1, 0)和(1−kk,+∞)上,f′(x)>0,在区间(0,1−kk)上,f′(x)<0,
即函数f(x)的单调递增区间为(−1, 0)和(1−kk,+∞),单调递减区间为(0, 1−kk);
当k=1时,f′(x)=x21+x,f(x)的递增区间为(−1, +∞),
当k>1时,由f′(x)=x(kx+k−1)1+x=0,得x1=0,x2=1−kk∈(−1,0),
∴ 在区间(−1,1−kk)和(0, +∞)上,f′(x)>0,在区间(1−kk,0)上,f′(x)<0,
即函数f(x)的单调递增区间为(−1,1−kk)和(0, +∞),单调递减区间为(1−kk,0).
【答案】
解:(1)∵ e=ca=33,2c=2,
∴ a=3,则b=a2−c2=2,
∴ 椭圆的方程为x23+y22=1.
(2)设A(x1, y1),B(x2, y2),
∵ OA→⊥OB→,∴ OA→⋅OB→=0,
即x1x2+y1y2=0.
由x2a2+y2b2=1,y=−x+1,消去y得(a2+b2)x2−2a2x+a2(1−b2)=0.
由Δ=(−2a2)2−4a2(a2+b2)(1−b2)>0,得a2+b2>1.
又∵ x1+x2=2a2a2+b2,x1x2=a2(1−b2)a2+b2,
∴ y1y2=(−x1+1)(−x2+1)=x1x2−(x1+x2)+1.
由x1x2+y1y2=0,得2x1x2−(x1+x2)+1=0.
∴ 2a2(1−b2)a2+b2−2a2a2+b2+1=0,整理得a2+b2−2a2b2=0.
∵ b2=a2−c2=a2−a2e2,代入上式得2a2=1+11−e2,
∴ a2=121+11−e2.
∵ 12≤e≤22,
∴ 14≤e2≤12,∴ 12≤1−e2≤34,
∴ 43≤11−e2≤2,∴ 73≤1+11−e2≤3,
∴ 76≤a2≤32,符合条件a2+b2>1,
由此可得426≤a≤62,∴ 423≤2a≤6,
故椭圆长轴长的最大值为6.
【考点】
直线与椭圆结合的最值问题
椭圆的定义
【解析】
此题暂无解析
【解答】
解:(1)∵ e=ca=33,2c=2,
∴ a=3,则b=a2−c2=2,
∴ 椭圆的方程为x23+y22=1.
(2)设A(x1, y1),B(x2, y2),
∵ OA→⊥OB→,∴ OA→⋅OB→=0,
即x1x2+y1y2=0.
由x2a2+y2b2=1,y=−x+1,消去y得(a2+b2)x2−2a2x+a2(1−b2)=0.
由Δ=(−2a2)2−4a2(a2+b2)(1−b2)>0,得a2+b2>1.
又∵ x1+x2=2a2a2+b2,x1x2=a2(1−b2)a2+b2,
∴ y1y2=(−x1+1)(−x2+1)=x1x2−(x1+x2)+1.
由x1x2+y1y2=0,得2x1x2−(x1+x2)+1=0.
∴ 2a2(1−b2)a2+b2−2a2a2+b2+1=0,整理得a2+b2−2a2b2=0.
∵ b2=a2−c2=a2−a2e2,代入上式得2a2=1+11−e2,
∴ a2=121+11−e2.
∵ 12≤e≤22,
∴ 14≤e2≤12,∴ 12≤1−e2≤34,
∴ 43≤11−e2≤2,∴ 73≤1+11−e2≤3,
∴ 76≤a2≤32,符合条件a2+b2>1,
由此可得426≤a≤62,∴ 423≤2a≤6,
故椭圆长轴长的最大值为6.
第17页 共18页 ◎ 第18页 共18页