- 2021-07-01 发布 |
- 37.5 KB |
- 31页

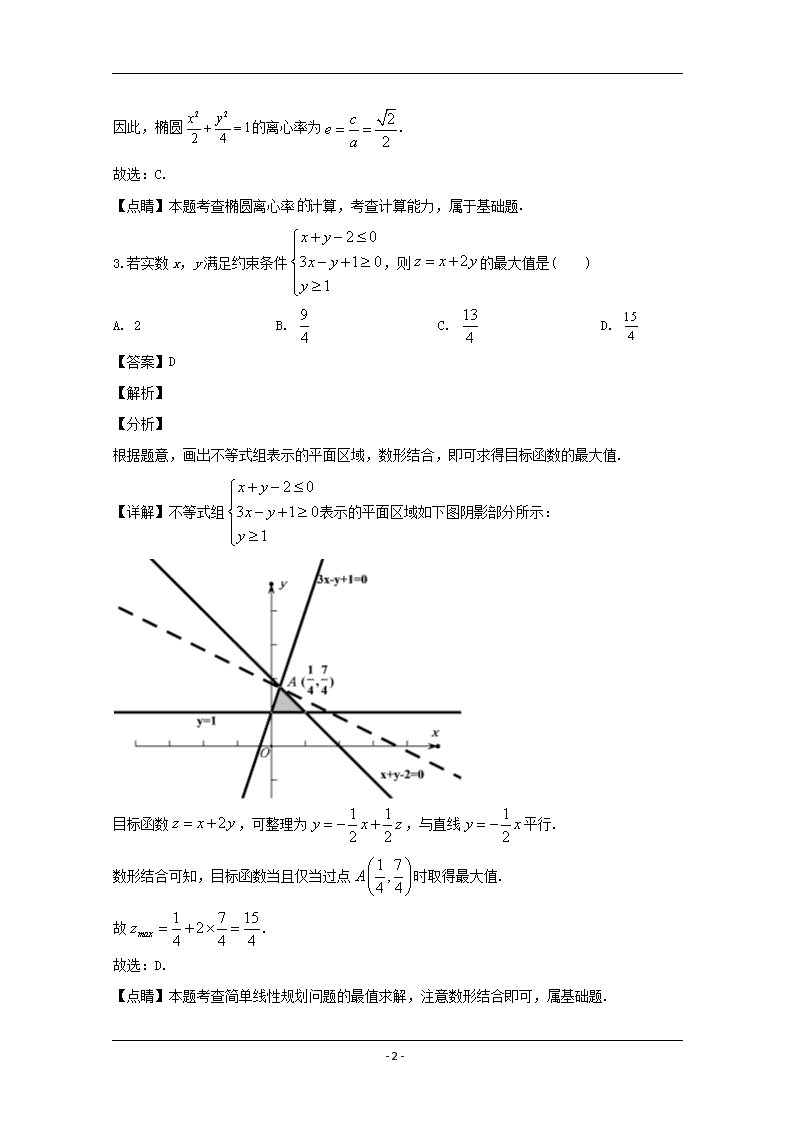

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
浙江省名校协作体2020届高三下学期联考数学试题 Word版含解
- 1 - 高三年级数学学科 第 I 卷(选择题部分,共 40 分) 一、选择题:本大题共 10 小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一 是符合题目要求的 1.已知集合 | 2 , | ln 1A x y x B x y x ,则 A B ( ) A. { | 2}x x B. { |1 2}x x C. { |1 2}x x D. { | 2}x x 【答案】A 【解析】 【分析】 根据二次根式的被开方数大于等于 0,即可求出集合 A ,根据对数函数的真数大于 0,即可求 出集合 B ,再根据交集的运算即可求出 A B . 【详解】解:由题意得, | 2 2A x y x x x , | ln 1 1B x y x x x , 则 2A B x x . 故选:A. 【点睛】本题考查集合的交集运算和函数的定义域,运用到二次根式的被开方数大于等于 0 和对数函数的真数大于 0,考查运算能力,属于基础题. 2.椭圆 2 2 12 4 x y 的离心率是( ) A. 2 B. 3 C. 2 2 D. 3 2 【答案】C 【解析】 【分析】 根据椭圆的方程求得 a 、 c 的值,即可得出该椭圆的离心率的值. 【详解】在椭圆 2 2 12 4 x y 中, 2a , 2b ,则 2 2 2c a b , 因此,椭圆 2 2 12 4 x y 的离心率为 2 2 ce a . - 2 - 故选:C. 【点睛】本题考查椭圆离心率的计算,考查计算能力,属于基础题. 3.若实数 x,y 满足约束条件 2 0 3 1 0 1 x y x y y ,则 2z x y 的最大值是( ) A. 2 B. 9 4 C. 13 4 D. 15 4 【答案】D 【解析】 【分析】 根据题意,画出不等式组表示的平面区域,数形结合,即可求得目标函数的最大值. 【详解】不等式组 2 0 3 1 0 1 x y x y y 表示的平面区域如下图阴影部分所示: 目标函数 2z x y ,可整理为 1 1 2 2y x z ,与直线 1 2y x 平行. 数形结合可知,目标函数当且仅当过点 1 7,4 4A 时取得最大值. 故 1 7 1524 4 4maxz . 故选:D. 【点睛】本题考查简单线性规划问题的最值求解,注意数形结合即可,属基础题. 4.某几何体的三视图如图所示,则该几何体的体积是( ) - 3 - A. 35 B. 40 C. 40 2 D. 48 【答案】B 【解析】 【分析】 由三视图还原出几何体的直观图,可知几何体为四棱柱,再利用棱柱的体积公式,结合题给 数据,即可求出几何体的体积. 【详解】解:由题给的三视图可得,该几何体为如下图: 即为直四棱柱 ABFE DCGH , 4, 1AB EF , 4BF BC , 则底面 ABFE 的面积为: 1 4 4 102S , 棱柱的高: 4h BC , 该几何体的体积为: 10 4 40V Sh . 故选:B. 【点睛】本题考查由三视图求几何体的体积,涉及棱柱的体积公式,画出几何体的直观图是 解题的关键. - 4 - 5.若 a,b∈R.则“关于 x 的方程 2 0x ax b 有两个不等实数根”是“a >|b|+1”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 【答案】B 【解析】 【分析】 若已知关于 x 的方程 2 0x ax b 有两个不等实数根,由根的判别式得出 2 4a b ,由于 a , b R ,可取 0, 1a b ,进行验算即可判断不能推出 1a b ,反之已知 1a b ,则 4 4 4a b ,利用 22 0a ,可得出 2 4a b ,则 ,可知能推出方程 2 0x ax b 有两个不等实数根,最后根据充分条件和必要条件的定义进行判断即可得出答案. 【详解】解:由题可知, a ,b R , 若已知关于 x 的方程 2 0x ax b 有两个不等实数根, 则 2 4 0a b ,即 2 4a b , 取 0, 1a b 时满足 2 4a b ,即 ,则方程 2 0x ax b 有两个不等实数根, 但此时 1a b ,故充分条件不成立; 反之,若已知 1a b ,即 1a b ,则 4 4 4a b , 由于 22 0a ,即 2 4 4a a , 所以 2 4a b ,则有 2 4a b ,即 ,则方程 2 0x ax b 有两个不等实数根, 故必要条件成立; 所以“关于 x 的方程 2 0x ax b 有两个不等实数根”是“ 1a b ”的必要不充分条 件. 故选:B. 【点睛】本题考查充分条件和必要条件的判断,利用一元二次方程根和判别式的关系是解题 的关键. 6.函数 2 xx x xey e 的图象大致是( ) - 5 - A. B. C. D. 【答案】A 【解析】 【分析】 利 用 定 义 法 判 断 函 数 的 奇 偶 性 , 得 出 f x 为 奇 函 数 , 排 除 C 和 D , 由 于 2 2 2x x x x x x e e x e e f x e e ,当 3x ,求得 3 0f ,得出原函数图象逼近 时, 图象单调递减,故 A 正确. 【详解】解:由于函数 2 xx xf x e xey , 则 2 xx xf x ee fx , 所以 f x 为奇函数,则图象关于原点对称,排除 C 和 D, 由于 2 2 2x x x x x x e e x e e f x e e , 当 3x 时, 3 3 3 3 3 3 2 6 82 2 2 6 4 0x x x xe e x e e e e ee e e , 即 3 0f ,即原函数图象逼近 时,切线的斜率小于 0, - 6 - 所以原函数图象逼近 时,图象单调递减,故 A 正确. 故选:A. 【点睛】本题考查根据函数解析式识别函数图象,利用定义法判断奇偶性和利用导数法判断 单调性进行排除. 7.随机变量 的分布列如下表所示,若 1 3E ,则 3 1D ( ) -1 0 1 p 1 2 a b A. 4 B. 5 C. 6 D. 7 【答案】B 【解析】 【分析】 由于 1 3E ,利用随机变量的分布列列式,求出 a 和 b ,由此可求出 D ,再由 3 1 9D D ,即可求出结果. 【详解】解:根据题意,可知: 1 12 a b ,则 1 2a b , 1 3E ,即: 1 1 2 3b , 解得: 1 6b , 1 3a , 2 2 21 1 1 1 1 1 51 0 13 2 3 3 3 6 9D , 则 53 1 9 9 59D D , 所以 3 1 5D . 故选:B. 【点睛】本题考查离散型随机变量的方差的求法,以及离散型随机变量的分布列、数学期望 等知识,考查运算求解能力. - 7 - 8.已知函数 | |f x x x a 的图象与 3 1g x ax 的图象有三个不同的交点,则实数 a 的 取值范围是( ) A. 1 , 2 B. 3 3 ,+ C. 34 1 3 , D. 1 3( , )2 3 【答案】A 【解析】 【分析】 当 0a 时,根据函数的图象知 ( )f x 和 ( )g x 的图象不可能有三个不同的交点,故舍去.当 0a 时,根据 ( )f x 和 ( )g x 相切时的图象即可得到 a 的取值范围. 【详解】当 0a 时,如图所示: ( )f x 和 ( )g x 的图象不可能有三个不同的交点,故舍去. 当 0a 时, ( )f x 和 ( )g x 相切时,如图所示: ( ) 3 1x x a ax ,即 2 4 1 0x ax . - 8 - 216 4 0a ,解得: 1 2a . 所以当 1 2a 时, ( )f x 和 ( )g x 的图象有三个不同的交点. 故选:A 【点睛】本题主要考查函数图象的交点个数,同时考查了分类讨论的思想,根据题意画出图 象为解题的关键,属于中档题. 9.已知矩形 , 4, 2,ABCD A AD EB 为 AB 中点,沿直线 DE 将 ADE 翻折成 PDE△ ,直 线 PB 与平面 BCDE 所成角最大时,线段 PB 长是( ) A. 7 43 B. 5 43 C. 7 42 D. 5 42 【答案】C 【解析】 【分析】 取CD 的中点 F ,连接 AF 交于 DE 的中点O ,AF DE ,进而有 DE 平面 POF ,过点 P 作 PQ AF 于点Q ,可证 PQ 平面 BCDE ,连接 BQ ,设直线 PB 与平面 BCDE 所成的 角为 ,平面 PDE 与平面 BCDE 所成的角为 ,根据条件可知 ,AO DE PO DE , PQ 平 面 BCDE , ,PBQ POQ , 通 过 边 长 关 系 求 出 2 cosOQ , 2 sinPQ , 2 2 cosAQ AO OQ , 以 及 利 用 余 弦 定 理 求 出 22 8 2 2 cosBQ ,从而得出 2 2 2 22 2 sin tan 8 2 2 cos PQ BQ ,根据同角 三角函数关系和换元法令 2cos 6 4,8t ,得出 2 4tan 1 32 8t t ,再根据基本 不等式时得出当 4 2 cos 2 2 3t 时, 2tan 取得最大值,从而可求出线段 PB 长 - 9 - 【详解】解:取CD 的中点 F ,连接 AF 交于 DE 的中点 O , 在矩形 ABCD 中, 4, 2,AB AD E 为 AB 中点, 所以四边形 AEFD 为正方形, AF DE , 所以 , ,PO DE OF DE PO OF O , 故 DE 平面 POF ,在平面 POF 内过点 P 作 PQ AF 于点Q , 则 ,DE PQ DE AF O ,所以 PQ 平面 BCDE ,连接 BQ , 设直线 PB 与平面 BCDE 所成的角为 ,即 PBQ 设平面 PDE 与平面 BCDE 所成的角为 , ,OF DE PO DE ,所以 POQ , 所以 2 2, 2DE PO AO , 所以在 Rt POQ△ 中, 2 sin , 2 cosPQ OQ , 则 2 2 cosAQ AO OQ , 在 ABQ△ 中, 4, 4AB BAQ , 则由余弦定理得出: 22 8 2 2 cosBQ , 则有 2 2 2 22 2 sin tan 8 2 2 cos PQ BQ 2 2 2sin 8 2 2cos 4cos 2 2 sin cos 2cos 5 2 2 1 cos cos 2cos 5 2 2cos 61 cos 2cos 5 , 令 2cos 6 4,8t ,则 6cos 2 t , 即: 2 4tan 1 32 8t t , 当直线 PB 与平面 BCDE 所成角 最大时, 2tan 最大, - 10 - 即 2 4tan 1 32 8t t 取得最大值时,当且仅当 32t t , 此时 4 2 cos 2 2 3t , 所以, 2 22 2 sin 8 2 2 cosPB 7 212 4cos 8 2 2 , 即 7 42PB . 故选:C. 【点睛】本题考查线面角和二面角的定义,还运用余弦定理和利用基本不等式求最值,还涉 及同角三角函数关系和换元法,考查转化思想和化简运算能力. 10.数列{ }na 满足 *3 1 10 1, N ,n n n na a a a n S , 表示数列 1 na 前 n 项和,则下列选项 中错误..的是( ) A. 若 1 20 3a ,则 1na B. 若 1 2 13 a ,则{ }na 递减 C. 若 1 1 2a ,则 1 14 2n n S a D. 若 1 2a ,则 2000 2 3S 【答案】D 【解析】 【分析】 对于选项 A,令 3 1f x x x , 0,1x ,利用导数求出 0,1f x 即可;对于选项 B, 首 先 得到 当 3 ,13x 时 有 3 3 1 13 3f f x f , 然 后结 合 1 2 13 a 和 2 1a a 可得出{ }na 递减;对于选项 C,证明 1 1 1 14 n n na a a 即可;对于选项 D,证明 - 11 - 1 1 7 1 1 6n n na a a 即可. 【详解】对于选项 A,令 3 1f x x x , 0,1x 则 23 1f x x ,所以 f x 在 30, 3 骣琪琪桫 上单调递减,在 3 ,13 上单调递增 因为 3 2 30 1, 1 0, 1 13 9f f f ,所以 0,1f x 所以当 1 20, 0,13a 时 1na ,故 A 正确 对于选项 B, 3 2 1 2 1 1 1n n n n n nna a a aa a a 因为 1 2 13 a ,所以 2 1 1 1 0a a ,所以 2 1a a 因为 3 1f x x x 在 3 ,13 上单调递增, 所以当 3 ,13x 时有 3 3 1 13 3f f x f 所以 1 2 3 2 3 31 9 3na a a a , 所以{ }na 递减,故 B 正确 对于选项 C,令 3 9 1, 05g x x x x 则 2 93 5g x x ,易得 min 15 6 151 05 25g x g 所以 3 9 1 05n na a ,所以 3 41 5n n na a a ,即 1 4 5n na a 所以 1 1 1 14 n n na a a 所以 1 2 2 1 3 2 1 1 1 1 1 1 1 1 1 1 1 1 14 4 + + 1 1 14 24 4n n nn n n S aa a a a a a a a aa a - 12 - 故 C 正确 对于选项 D,因为 1 2a ,所以 3 2 1 2 1 2 1 0n n nn n na a aa a a 所以 2 2 1 1 4n n n na a a a 令 3 8 1, 4h x x x x ,则 23 8h x x 易得 4 0h x h ,所以 3 8 1 0n na a ,所以 3 1 7n n na a a ,即 1 7n na a 所以 1 1 7 1 1 6n n na a a 所以 2 2 3 3 4 1 1 1 1 1 7 1 1 7 1 1 7 1 1+ +2 2 6 6 6n n n na a a a a a a aS 2 1 1 1 7 1 1 1 7 1 1 1 1 2 2 6 2 6 7 2 6 3n na a a 故 D 错误 故选:D 【点睛】本题考查的是数列的综合问题,解答的关键是结合导数的知识,构建合适的不等式, 属于难题. 第Ⅱ卷(非选择题部分,共 110 分) 二、填空题:本大题共 7 小题,多空题每题 6 分,单空题每题 4 分,共 36 分. 11.已知复数 z 满足 1 2 3 4 (i z i i 为虚数单位),则复数 z=________;|z|=________. 【答案】 (1). 1 2i (2). 5 【解析】 【分析】 根据复数的运算法则即可化简求得复数 z ,再利用复数的模长公式求解即可. 【详解】因为 1 2 3 4i z i ,故可得 3 4 1 23 4 5 10 1 21 2 1 2 1 2 5 i ii iz ii i i . 又 2 21 2 5z . 故答案为: 1 2i ; 5 . 【点睛】本题考查复数的运算法则,以及复数模长的求解,属综合基础题. - 13 - 12.二项式 3( )nxx 的展开式中,各项系数之和为 64,则 n=________;展开式中的常展开 式中的常数项是________. (用数字作答) 【答案】 (1). 6 (2). 135 【解析】 【分析】 令 1x ,求出展开式各项的系数和,建立关于 n 的方程,进而求出展开式的通项,令 x 的指 数为 0,求出项数,即可得出结论. 【详解】对于二项式 3( )nxx ,令 1x , 得各项的系数和为 2 64, 6n n , 二项式 63( )xx 的展开式中, 通项为 3 66 6 2 1 6 6 3( ) ( ) ( 1) 3 kk k k k k k kT C x C xx , 0,1,2, 6k ,令 3 6 0, 42 k k , 所以展开式中常数项为 2 4 63 135C . 故答案为:6,135. 【点睛】本题考查二项展开式定理以及性质,利用赋值法是解题的关键,熟记展开式的通项, 属于基础题. 13.已知椭圆 2 2 14 x y .点 E 为椭圆在第一象限内一点,点 F 在椭圆上且与点 E 关于原点对 称,直线 1 0x y 与椭圆交于 A,B 两点,则点 E,F 到直线 x+y-1=0 的距离之和的最大值 是________;此时四边形 AEBF 的面积是________. 【答案】 (1). 10 (2). 8 5 5 【解析】 【分析】 根据题意,设出 ,E F 两点坐标,利用点到直线的距离公式,求得距离之和的表达式,结合 E - 14 - 点在椭圆上坐标满足椭圆方程,利用柯西不等式即可求得距离之和的最大值;联立椭圆方程 和 1 0x y ,求得 ,A B 两点坐标,即可求得 AB ,则四边形的面积可得. 【详解】根据题意,作图如下: 不妨设 0 0,E x y ,则 0 0,F x y , 故 ,E F 到直线 1 0x y 的距离之和 0 0 0 01 1 2 x y x yd 因为点 E 是椭圆上位于第一象限的点,根据直线划分平面,以及点 E 位于直线 AB 的右上侧, 故可得: 0 0 1 0x y ,且 0 0 1 0x y , 则 0 0 0 0 0 0 1 1 2 2 x y x yd x y . 又因为点 E 在椭圆上,故 2 2 0 04 4x y , 由柯西不等式可得: 2 22 2 2 0 0 0 0 14 1 2x y x y , 即 2 0 0 5x y ,解得 0 0 5x y ,当且仅当 0 0 4 5 5,5 5x y 时取得等号. 故 0 02 2 5 10d x y ; 联立椭圆方程 2 2 14 x y 与直线方程 1 0x y , - 15 - 可得 25 8 0x x ,解得 8 30,1 , ,5 5A B , 故可得 2 28 8 8 2 5 5 5AB . 故四边形 AEBF 的面积 1 8 5 2 5S AB d . 故答案为: 10 ; 8 5 5 . 【点睛】本题考查椭圆中四边形面积的求解,涉及椭圆中范围问题的求解,涉及柯西不等式 的利用,属综合中档题. 14.在锐角 ABC 中,已知内角 A,B,C 的对边分别是 a,b,c, 5 6A B ,则 b a 的取值 范围是________.若这个三角形中的 A,B 同时满足 tanA=2tanB,则 sin A B ________. 【答案】 (1). 3 2 3,2 3 (2). 1 6 【解析】 【分析】 (1)利用正弦定理将 b a 转化为 sin sin B A ,然后将 B 转化为 A ,利用 A 的取值范围,求得 b a 的取 值范围. (2)利用 tan 2tanA B 以及 5 6A B ,结合两角差的正切公式,求得 tan A 的值,将 sin A B 转化为含 tan A 的表达式的形式,由此求得 sin A B 的值. 【详解】(1)由正弦定理得 5 1 3sin cos sinsin 1 36 2 2 sin sin sin 2tan 2 A A Ab B a A A A A . 由于三角形 ABC 是锐角三角形,所以 0, 2 3 25 0,6 2 A A B A ,所以 1 3tan 3, , 0,2tan 6A A ,所以 3 2 3,1 3 2 2 3tan 2A . - 16 - (2)由于 5tan tan5 6tan 2tan 2tan 2 56 1 tan tan6 A A B A A ,化简得 2tan 3 3 tan 2 0A A ①,由于 A 为锐角,所以 tan 0A ,所以①解得 3 3 35tan 2A . 由 tan 2tanA B 可得 sin 2sin sin cos 2cos sincos cos A B A B A BA B , 所以 sin sin cos cos sinA B A B A B 5cos sin cos sin 6A B A A 21 3 1 3cos cos sin cos sin cos2 2 2 2A A A A A A 2 2 2 2 1 3 1 3cos sin cos tan2 2 2 2 cos sin 1 tan A A A A A A A ,将 3 3 35tan 2A 代入上式并化简得 2 1 3 tan 12 2 1 tan 6 A A ,即 1sin 6A B . 故答案为:(1) 3 2 3,2 3 ;(2) 1 6 . 【点睛】本小题主要考查利用正弦定理进行边角互化,考查三角恒等变形,考查化归与转化 的数学思想方法,考查运算求解能力,属于中档题. 15.设正数 a,b 满足, 1 13 16a ba b ,则 a b b a 的最大值是________. 【答案】18 【解析】 【分析】 变形已知 1 3( 3 ) ( ) 16a b a b ,利用基本不等式构造 a b b a , 由 1 3 1 316 ( 3 ) ( ) 2 ( 3 )( )a b a ba b a b 化简可得解. - 17 - 【详解】 1 13( ) 16a ba b , 1 3( 3 ) ( ) 16a b a b 1 3 1 316 ( 3 ) ( ) 2 ( 3 )( )a b a ba b a b 8 10 3( )a b a b , 3( ) 54b a a b , 18b a a b 当且仅当 1 33 = 8a b a b 即 7 3 5 2 3 5 2 a b 或 7+3 5 2 3 5 2 a b 时等号成立. 故答案为:18 【点睛】本题考查通过拼凑法利用基本不等式求最值. 拼凑法的实质在于代数式的灵活变形,拼系数、凑常数是关键. (1)拼凑的技巧,以整式为基础,注意利用系数的变化以及等式中常数的调整,做到等价变形; (2)代数式的变形以拼凑出和或积的定值为目标(3)拆项、添项应注意检验利用基本不等式的 前提. 16.已知平面向量 , ,a b c , 1| | | | 1, , 22a b a b a c ,若对于任意的向量 d 均有| |d c 的 最小值为 2 | |d a ,则| | | |d a d b 的取值范围是________. 【答案】 2 2 3,2 2 3 【解析】 【分析】 设向量 , , ,a b c d 的始点为原点O ,终点分别为 , , ,A B C D ,取 1 3(1,0), ( , )2 2a b ,则点C 在直线 2x 上,设点 D 到直线 2x 的距离为 d ,则| |d c | |CD d ,所以 | | 2 2 AD d , 设 ( , )D x y ,可得点 D 的轨迹方程为 2 2 12 x y ,再根据椭圆的定义可得结果. 【详解】设向量 , , ,a b c d 的始点为原点O ,终点分别为 , , ,A B C D , 因为 1| | | | 1, , 22a b a b a c , - 18 - 取 1 3(1,0), ( , )2 2a b ,则由 2a c 可知点C 在直线 2x 上, 设点 D 到直线 2x 的距离为 d ,则| |d c | |CD d , 根据题意得 2 | | 2 | |d a AD d , 即 | | 2 2 AD d , 设 ( , )D x y ,则 2 2( 1) 2 | 2| 2 x y x , 化简得 2 2 12 x y , 所以动点 D 的轨迹是以 A (1,0) 为焦点,直线 2x 为准线的椭圆, 设另一个焦点为 1A ,则 1( 1,0)A , 易知点 1 3( , )2 2B 在椭圆内, 如图所示: 所以| | | |d a d b | | | |DA DB 1 12 2 | | | | 2 2 | |DA DB A B 2 21 32 2 ( 1 ) ( )2 2 2 2 3 ,当 D 为 1BA 的延长线与椭圆的交点时取得等号, | | | |d a d b | | | |DA DB 12 2 | | | |DA DB 12 2 | | 2 2 3A B , - 19 - 当 D 为 1A B 的延长线与椭圆的交点时取得等号, 所以| | | |d a d b 的取值范围是 2 2 3,2 2 3 . 故答案为: 2 2 3,2 2 3 【点睛】本题是平面向量和椭圆的综合题,根据平面向量的几何意义得到动点 D 的轨迹为椭 圆是解题关键,考查了根据椭圆的定义求动点到定点的距离之和的最值,属于难题. 17.已知函数 | | 1 lnx af x xe x ,当 1,x 时, f x 的最小值为0 ,且对任意的 1 ,12x ,不等式 22cosax m x 恒成立,则实数 m 的最大值是________. 【答案】2 【解析】 【分析】 根据题意,由 f x 的最小值为 0 分析可得 1a ,再对不等式变形可得 22cos x x m , 构造函数 22cosg x x x ,求得最小值为 0 2g ,即可得到结论. 【详解】由题意, 1 ln ,1 ln 1 ln , x a x a a x xe x x af x xe x xe x x a , 当 1a 时, 1 lnx af x xe x ,此时 11 x af x x e x , 当 1,x 时, 0f x 恒成立,则 f x 在 1,x 上单调递增, 所以, f x 的最小值为 11 1 0af e ,解得 1a . 当 1a 时, 1 ln , 1 ln , x a a x xe x x af x xe x x a , 当 x a≥ 时,此时 1 lnx af x xe x , 11 0x af x x e x 恒成立, 所以,函数 f x 的最小值为 1 ln 0a af a ae a ,解得 1a (舍), 当 x a 时,此时 1 lna xf x xe x , 11 0a xf x x e x 恒成立, 所以,函数 f x 的最小值为 1 ln 0a af a ae a ,解得 1a (舍). 综上,当 1,x 时, f x 的最小值为0 时,此时 1a , - 20 - 所以,不等式 22cos x m x 对 1 ,12x 恒成立,即 22cos x x m , 令 22cosg x x x ,则 2 2sin 2 sing x x x x x , 令 sinh x x x ,则 1 cos 0h x x 恒成立,即 h x 在 R 上单调递增,又 0 0h , 所以,当 1 02 x 时, 0h x ,即 0g x ;当 0 1x 时, 0h x ,即 0g x . 即 g x 在 1 ,02 上单调递减,在 0,1 上单调递增, 所以, g x 在 0x 处取得最小值,此时最小值为 0 2g , 所以, 2m ,即实数 m 的最大值为 2 . 故答案为: 2 . 【点睛】本题考查利用导数研究函数的单调性,考查分类讨论思想,构造函数,考查不等式 恒成立,属于中档题. 三、解答题:本大题共 5 小题,共 74 分.解答应写出文字说明、证明过在演算步骤 18.已知关于 x 的函数 22 3sin 2sin cos ,f x x x x m m R ,其图象过点 ( ,2)12 . (1)求实数 m 的值; (2)设 0, , 2 1 2f ,求 cos 的值. 【答案】(1) 3 ;(2) 3 15 8 . 【解析】 【分析】 (1)根据题意化简函数 f x ,再由函数图象过点 ,212 ,即可得到 3m . (2)根据 2 1 2f ,可得 1sin 3 4 ,再由 0, 可得 15cos 3 4 , 再将 cos cos 3 3 ,即可得到结论. 【详解】由题意, 22 3sin 2sin cos 3 1 cos2 sin 2f x x x x m x x m , - 21 - 即 2sin 2 33f x x m . (1)因函数 f x 其图象过点 ,212 ,即 2sin 3 212 6 3f m , 解得 3m . (2)由 12sin2 3 2f ,即 1sin 3 4 , 又 0, ,则 4,3 3 3 ,而 1sin 3 4 ,则 15cos 3 4 , 所以, cos cos cos cos sin sin3 3 3 3 3 3 即 15 1 1 3 3 15cos 4 2 4 2 8 . 【点睛】本题考查了二倍角的正弦、余弦函数公式,两角和与差的余弦函数公式,灵活运用 三角函数的恒等变换把函数解析式化为一个角的余弦函数是解本题的关键. 19.如图,在四棱锥 P-ABCD 中,底面 ABCD 为直角梯形 90ADC ,BC//A D , 1, 2,CD BC AD PAB 为正三角形,M 为 PD 中点. (1)证明:CM//平面 PAB; (2)若二面角 P-AB-C 的余弦值为 3 3 ,求直线 AD 与平面 PBD 所成角的正弦值. 【答案】(1)证明见解析;(2) 3 3 . 【解析】 - 22 - 【分析】 (1)根据题意,取 AD 的中点为 E ,连接 EM ,EC ,利用中点可得平面 / /PAB 平面 MEC , 进而可得结论; (2)根据题意,取 AB 的中点 F ,连接 PE ,BE ,EF ,计算可得 PE EF ,进而可得 PE 平面 ABCD ,建立坐标系,利用空间向量计算即可. 【详解】(1)证明:取 AD 的中点为 E ,连接 EM , EC ,如图: 由题意, ABCD 为直角梯形, 1BC CD , 2AD , M 为 PD 中点, ∴ ME PA , / /EC AB , 又 PA AB A , ME EC E , ∴平面 / /PAB 平面 MEC ,而CM 平面 MEC ,CM 平面 PAB , 故 / /CM 平面 PAB . (2)由题意,取 AB 的中点 F ,连接 PE , BE , EF ,如图: 因 ABE 为等腰直角三角形, PAB 为正三角形,则 EF AB , PF AB ,即 AB 平面 PEF ,即 PE AB 即二面角 P AB C- - 的平面角为 PFE ,则 3cos 3PFE ,又 2AB ,则 6 2PF , 2 2EF ,由余弦定理可得 1PE ,则 2 2 2EF PE PF ,即 PE EF ,而 EF AB F ,所以, PE 平面 ABCD ,由 ABCD 为直角梯形, - 23 - 所以,以 , ,EB ED EP 分别为 , ,x y z 轴建立空间直角坐标系,则 0, 1,0A , 0,0,1P , 0,1,0D , 1,0,0B ,则 0,2,0AD , 0,1, 1PD , 1,0, 1PB 设平面 PBD 的一个法向量为 , ,n x y z , 由 0 0 n PD n PB ,即 0 0 y z x z ,取 1z ,所以 1x y , 所以,平面 PBD 的一个法向量为 1,1,1n , 所以 2 3sin cos , 32 3 n AD , 即直线 AD 与平面 PBD 所成的正弦值为 3 3 . 【点睛】本题考查了线面平行的判定,空间向量与线面角的计算,属于中档题. 20.已知数列 na 前 n 项和为 nS ,且满足 1 1 *N1, 2,n n na a S S n n . (1)求数列 na 的通项公式; (2)记 nT 为 1n na S 的前 n 项和 n N ,证明: 3 1 4 2 1nT n n . 【答案】(1) 1, 1 1 , 21 n n a nn n ;(2)证明见解析. 【解析】 【分析】 (1)根据题意可得 1 nS 为首项与公差都为1的等差数列,进而可得数列 na 的通项公式; (2)根据(1)可得 1 2 1 1n na S n n ,即 2 1 3 2 1n n nT a S a S a S ,再利用数学归 纳法证明即可. 【详解】(1)当 2n 时,由 1 1n n n n na S S S S ,即 1 1 1 1n n n n n n S S S S S S , - 24 - 所以, 1 1 1 1 n nS S ,又 1 1 1 1 1S a ,故数列 1 nS 为首项与公差都为1的等差数列, 所以, 1 n nS ,即 1 nS n ,故 1 1 1n n na S S n n ,而 1 1a , 故数列 na 的通项公式: 1, 1 1 , 21 n n a nn n . (2)由(1)可得 1 2 1 1n na S n n , 所以, 2 1 3 2 1 2 2 2 1 1 1 1 2 2 3 1n n nT a S a S a S n n 要证明 3 1 4 2 1nT n n , 即证明 2 2 2 1 1 1 1 2 2 1 23 3 4 11n n n n . 数学归纳法证明: 当 1n 时,左边 2 1 1 1 2 2 ,右边 3 1 1 4 2 1 2 2 ,不等式成立; 假设当 n k 时, 2 2 2 1 1 1 1 2 2 1 23 3 4 11k k k k 成立, 那么当 1n k 时, 左边 22 2 2 1 1 1 1 1 2 2 3 1 1 1 1k k k k 2 2 2 3 1 1 3 2 4 2 1 41 2 2 1 2 k k k k k k k k k 2 2 2 13 3 4 42 1 2 2 1 2 k kk k k k k k k k 3 1 4 2 1 1 1k k 右边. 即当 1n k 时,不等式也成立; - 25 - 综上,当 n N 时,不等式 2 2 2 1 1 1 1 2 2 1 23 3 4 11n n n n 成立, 故 3 1 4 2 1nT n n . 【点睛】本题考查了递推关系的应用、数学归纳法、不等式的性质,考查了推理能力与计算 能力,属于中档题. 21.如图,已知椭圆 C: 2 2 12 x y 过原点的直线与椭圆交于 A,B 两点(点 A 在第一象限),过 点 A 作 x 轴的垂线,垂足为点 0,0E x ,设直线 BE 与椭圆的另一交点为 P,连接 AP 得到直线 l,交 x 轴于点 M,交 y 轴于点 N. (1)若 0 1x ,求直线 AP 的斜率; (2)记 , ,ABP OEP OMN 的面积分别为 S1,S2,S3,求 1 2 3 2S S S 的的最大值. 【答案】(1) 2 ;(2) 1 2 . 【解析】 【分析】 (1)根据 0 1x ,求出 , ,E A B 的坐标,再求出直线 BE 的方程,并与椭圆方程联立解得 P 的 坐标,最后用斜率公式可得直线 AP 的斜率; (2)设 1 1( , )P x y , 0 0( , )A x y ,则 0 0( , )B x y ,利用三角形的面积公式求出 1 2 0 02S S x y , 根据斜率公式和椭圆方程可得 PA 的斜率和直线 PA 的方程,进而求出 ,M N 的坐标和 3S ,最 后用基本不等式可求得结果. 【详解】(1)因为 0 1x ,所以 0 2 2y , - 26 - 所以 (1,0)E , 2(1, )2A , 2( 1, )2B , 所以直线 BE 的方程为: 2 020 ( 1)1 1y x ,即 2 2 1x y , 联立 2 2 2 2 1 12 x y x y ,消去 x 并整理得 210 4 2 1 0y y , 所以 1 2 2y , 2 2 10y ,所以 7 2( , )5 10P , 所以 2 2 2 10 271 5 APk . (2)设 1 1( , )P x y , 0 0( , )A x y ,则 0 0( , )B x y , 则 1 ABE APES S S 0 0 0 1 0 1 ( )2x y y x x , 因为 1 1( , )P x y 在直线 BE : 0 0 0 2xx y xy 上, 所以 0 1 1 0 0 2xx y xy ,所以 0 1 0 0 0 1 0 21 2 xS x y y yy 0 0 0 1x y x y , 因为 2 0 1 1 2S x y , 所以 1 2 0 0 0 1 0 1 0 02S S x y x y x y x y , 因为 2 2 1 1 0 1 0 2 2 1 0 1 0 1 0 o PA PB y y y y y yk k x x x x x x 2 2 1 0 2 2 1 0 1 11 1 12 2 2 x x x x , - 27 - 所以 0 0 0 0 1 1 2 2 2 PA PB xk yk y x , 所以直线 PA : 0 0 0 0 ( )xy y x xy , 所以 2 0 0 0 ( ,0)yM xx , 2 0 0 0 (0, )xN yy , 所以 2 2 0 0 3 0 0 0 0 1 ( )( )2 y xS x yx y 2 2 2 0 0 0 0 ( ) 2 x y x y , 所以 0 01 2 2 2 2 0 03 0 0 2 ( ) 2 x yS S x yS x y 2 2 0 0 2 2 2 0 0 2 ( ) x y x y 2 2 0 0 2 2 0 0 2 4 x y x y 1 2 , 当且仅当 0 0x y 6 3 时,等号成立. 所以 1 2 3 2S S S 的的最大值为 1 2 . 【点睛】本题考查了直线与椭圆的交点问题,考查了直线方程的点斜式和直线的斜率公式, 考查了基本不等式,考查了运算求解能力,属于中档题. 22.已知函数 ln x af x a xe a e x , a R (其中 e 为自然对数的底数). (1)当 1a 时,讨论函数 f x 的单调性; (2)当 0a 时,若不等式 lnf x a x 恒成立,求实数 a 的取值范围. 【答案】(1)函数 f x 在 R 上单调递增;(2) 1ea e . 【解析】 【分析】 (1)将 1a 代入解析式,并求得 f x ,令 1x xg x e 并求得 g x ;由 g x 的符 号可判断 g x 的单调性,进而求得 min 0g x ,即可由 f x 符号判断函数 f x 的单调 性; (2)根据不等式及函数 f x 的解析式,代入后化简变形,并令 xt a ,转化为关于t 的不等 - 28 - 式,分离常数后构造函数 ln t t t eh t te ,求得 h t 后,再构造函数 1 lng t t t e , 求得 g t ;由 g t 的符号可判断 g t 的单调性,进而可知存在 0 2 1 ,1t e 使得 0 0g t , 从而判断出 h t 的单调性与极值点,结合函数解析式求得 1 0 eh e h t e ,即可由恒成 立问题求得 a 的取值范围. 【详解】(1)当 1a 时,函数 xf x xe e x , 则 2 11 x x x xx e xe ef xx ee , 令 1x xg x e , 则 1xg x e ,令 0g x ,解得 0x , 所以当 0x 时, 1 0xg x e , 1x xg x e 在 0x 时单调递减, 当 0x 时, 1 0xg x e , 1x xg x e 在 0x 时单调递增, 即 min 1 2 00 xg x g e x , 所以 1 0 x x xef x e , 即函数 f x 在 R 上单调递增. (2)当 0a 时,不等式 lnf x a x 恒成立, 代入可得 ln ln x aa xe a e x a x , 因为 0a ,化简可得 ln ln x a xxe a e xa ,即 ln 0 x a x xxe a ae , 令 , 0xt ta ,所以 ,x at 则不等式可化为 ln 0tate e t t , 变形可得 ln t t t ea te , - 29 - 令 ln t t t eh t te , 则 2 2 1 1 ln 1 1 ln t t t tt te t t e e te t t t eth t t ete , 令 1 lng t t t e ,则 1 11 tg t t t , 令 0g t ,解得 1t , 当 0 1t 时, 0g t ,则 g t 在 0 1t 内单调递减, 当1 t 时, 0g t ,则 g t 在1 t 内单调递增, 而 1 1 1 ln1 2 0g e e , 2 2 1 13 0g e e e , 0g e , 所以存在 0 2 1 ,1t e 使得 0 0g t , 从而当 00,t t 时 0h t ,则 ln t t t eh t te 在 00,t t 时单调递增; 当 0,1t t 时, 0h t ,则 ln t t t eh t te 在 0,1t t 时单调递减; 当 1,t e 时, 0h t ,则 ln t t t eh t te 在 1,t e 时单调递增; 当 1,t 时, 0h t ,则 ln t t t eh t te 在 1,t 时单调递减. 则 ln t t t eh t te 在 0x t 或 x e 处取得最大值, 而 11 e eh e e e e , 0 00 00 ln t t t eh t t e , 因为 0 0g t ,即 0 01 ln 0t t e - 30 - 则 ln 1 10 0 10 0 00 0 0 0 00 ln t t e e e t t t e t ee eh t et t tt e , 综上可知, a 的取值范围为 1ea e . 【点睛】本题考查了导函数与函数单调性的关系,函数单调性、极值、最值的综合应用,由 导函数研究不等式恒成立问题,分离参数与构造函数法的综合应用,是高考的常考点,属于 难题. - 31 -查看更多